בשלישי האחרון מעבדות פרמילאב שבארצות הברית הודיעו שהמומנט המגנטי של המיואון אינו תואם את חישובים התאורטיים. הניסוי שנערך במדינת אילנוי מאשש את האנומליה שהתגלתה לפני מספר שנים אך לראשונה עומדת על וודאות של 4.25 סיגמה (שגיאה סטטיסטית הקרובה ל 1:100,000). האם זו עדות לכוח יסודי חדש בטבע?

ראו גם: רגע האמת הגיע – האם השבוע נתבשר על פיזיקה חדשה?
עשור חלף מאז פריצת הדרך האחרונה בפיזיקת החלקיקים ועדיין אין חדש תחת השמש. מצד אחד התגליות תואמות בדיוק מפליא למודל הסטנדרטי, מצד שני, אין ספק שהמודל אינו שלם. המקרה הייחודי של מעבדות פרמילב שבארצות הברית שונה בנוף המדעי משום שהפעם, אחרי שנים רבות נחשפה עדות משמעותית לפיזיקה חדשה. תוצאות הניסוי פורסמו ביום שלישי האחרון בכתב העת היוקרתי Physical Review Letters וכבר מעוררות מבוכה והתרגשות בקרב פיזיקאים ברחבי העולם. הניסוי הידוע בכינויו g-2 מדד את המקדם g של המומנט המגנטי של המיואון, אותו מקדם אחראי על מידת הסיבוב של המגנט הפנימי של החלקיק.
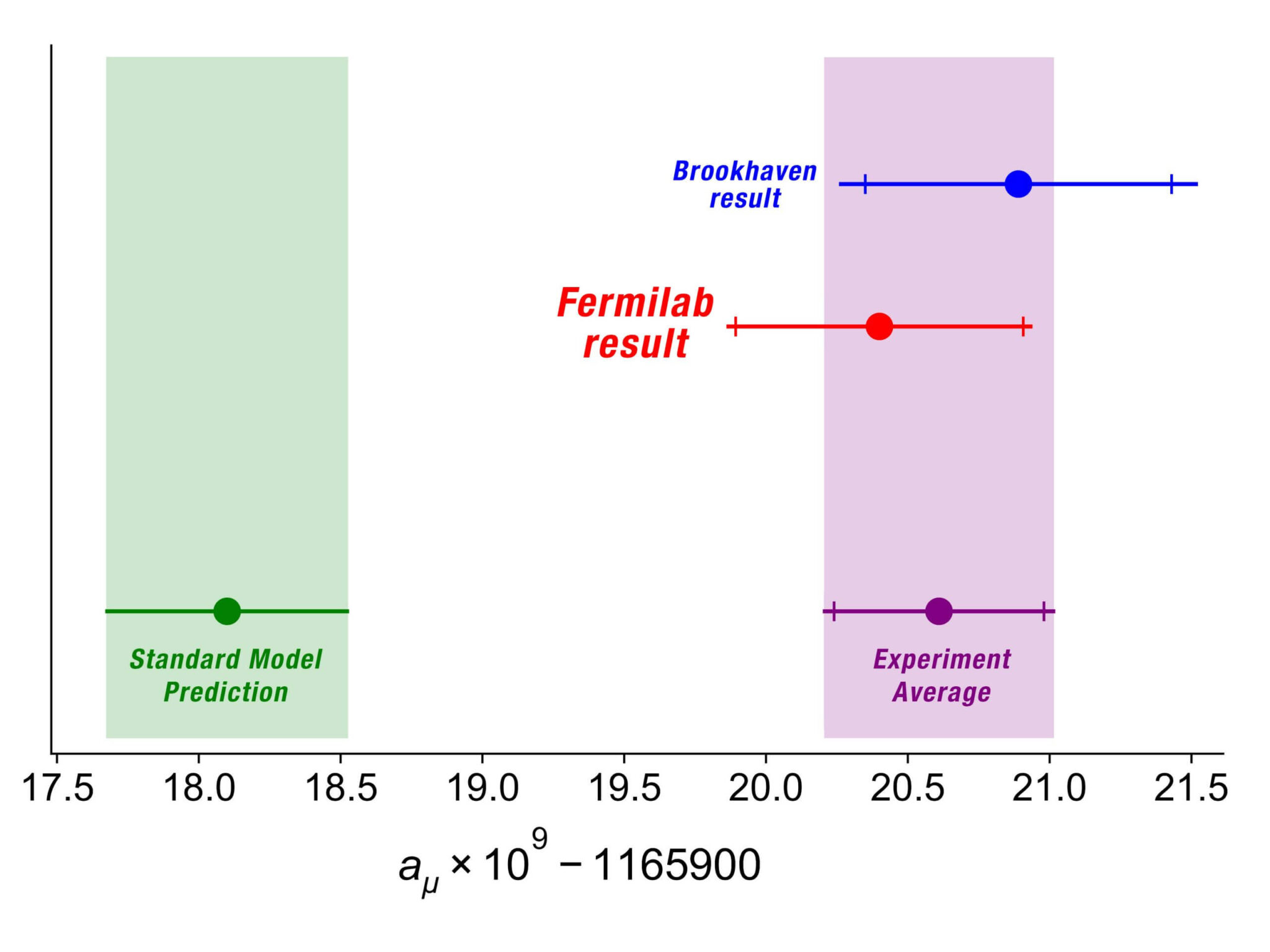
סטיה בין תוצאות הניסוי לחישובים התיאורטיים
התגלית משמעותית משום שהיא מאמתת בדיוק גבוה של 4.25 סיגמה (סבירות של אחד למאה אלף שמדובר בטעות סטטיסטית) את הסתירה בין תוצאות הניסוי לחישובים התאורטיים שפורסמו בעבר. פיזיקאים מרכזים מאמצים רבים כדי לחשב את הסיבוב הפנימי של החלקיקים בטבע עד כדי אובססיה. הסיבה לכך נעוצה בעובדה שמדובר בגודל פיזיקאלי שניתן למדוד ברגישות רבה ומשום שהוא מכיל מידע רב על הוואקום הקוונטי ביקום. כשפיזיקאים מתייחסים ל"וואקום", הם לא מתכוונים לריק מוחלט, אלא לסביבה בלי חלקיקים בכלל. הוואקום אומנם נשמע ריק לחלוטין אך הוא מלא בשדות קוונטים. על פי עיקרון האי וודאות קיים רעש תמידי בשדות הקוונטים המבוטא בחלקיקים הנוצרים ונעלמים באופן ספונטני. לכל חלקיק בטבע קיים שדה המתאר אותו, לפיכך כל חלקיק יכול להופיע בפתאומיות בוואקום ולהגיב עם חלקיקים בסביבתו, זאת כמובן בהתאם למודל הסטנדרטי. אומנם רבים מכנים חלקיקים אלו בתור "חלקיקים וירטואלים" אך השפעתם ניתנת למדידה משום שהם מגיבים עם המיואון (או כל חלקיק טעון אחר) ומשנים את גודלו של הפקטור g.
המומנט המגנטי המפורסם ביותר שנמדד שייך לאלקטרון. הדיוק התאורטי מופתי ועומד על ארבע עשרה ספרות אחרי הנקודה העשרונית. כל ניסוי שימדוד את המומנט המגנטי של האלקטרון יראה התאמה מלאה לתאוריה ויאשש את טבעו הקוונטי של היקום. יחד עם זאת, אנחנו יודעים שהמודל הסטנדרטי אינו שלם. הוא אינו מסביר את האנרגיה והחומר האפלים, לא מסביר את האוסילציות של חלקיקי הנייטרינו ולא מתאר כלל את כוח הכבידה. מסיבה זו פיזיקאים ראו לנכון לבחון את המומנט המגנטי של המיואון משום שהוא מגיב בסבירות ובעוצמה גדולה יותר מהאלקטרון (פי 40,000). אם המודל הסטנדרטי אינו שלם, אנומליה עשויה להתגלות בסבירות גבוהה דרך המיואון.
גם ב-CERN דיווחו על אנומליות
ואכן, התוצאות הניסיוניות לא תואמות את החישובים התיאורטיים שנערכו עד כה. המספר התאורטי למומנט המגנטי של המיואון עומד כיום על 2.00233183620 (עם שגיאה אפשרית ב-2 ספרות האחרונות אחרי הנקודה העשרונית). המספר שנמדד בניסוי הקודם שנערך במדינת ניו יורק בהחלט היה שונה אך הוודאות הייתה נמוכה יחסית (3.7 סיגמה, כלומר וודאות של אחד לעשרת אלפים). לקוראים הוותיקים נזכיר שלא מזמן המאיץ בסרן דיווח על אנומליה במדידות שנאספו בוודאות של 3.9 סיגמה אבל אחרי שנאספו עוד נתונים התוצאה נעלמה. לכן, פיזיקאים מעדיפים להחשיב תוצאה משמעותית כ"תגלית" רק אם הוודאות עומדת על 5 סיגמה לפחות (הסתברות של אחד ל-3.5 מיליון שמדובר בטעות). כיום, הניסוי שנערך במדינת אילנוי הראה שהמומנט המגנטי של המיואון עומד על 2.00233184122 (שוב עם שגיאה בשתי הספרות האחרונות אחרי הנקודה עשרונית עם דיוק של 4.25 סיגמה). זו התקדמות משמעותית אל עבר מה שנחשב כ"תגלית". החוקרים מקווים להשיג יעד זה לאחר שינתחו את שאר המדידות שנאספו בהרצה השלישית והרביעית של הניסוי. בפרמילב דיווחו שהם מקווים שהאנליזה תסתיים בקיץ הבא במטרה להגיע לוודאות של 5 סיגמה. קריס פולי, מדען בפרמילב מוסיף: "עד כה ניתחנו רק 6% מהנתונים שאספנו. ולמרות זאת, כבר מנתונים אלו אנחנו יכולים לראות אי התאמה בין המודל הסטנדרטי לבין מה שהטבע מספר לנו. אני מאמין שעוד נשמע חדשות מרגשות נוספות בשנים הקרובות".
חשוב לציין שאומנם השגיאה קטנה, אך בהחלט משמעותית כדי לטעון שמדובר בפיזיקה חדשה. מאיזו סוג? אין לדעת. יכול להיות שמודבר בחלקיק מאסיבי שנוצר בהסתברות נמוכה המגיב עם המיואון אך לא התגלה עדיין במאיצים. יכול להיות שמדובר בכוח חדש שטרם גילינו או בסוג נוסף של חלקיק היגס.
במסיבת העיתונאים של פרמילב ציינו שזו רק ההתחלה מבחינתם וכעת הם עומדים בפתחו של פרויקט שימשך לפחות כעשור. הפרויקט ימשיך לאסוף נתונים על המומנט המגנטי של המיואון ובמקביל יבחן את דרכי ההתפרקות של המיואון בניסוי המכונה mu2e. החוקרים מקווים למדוד בניסוי החדשני תהליכי התפרקות המוסברים רק על ידי תאוריות חדשות מעבר למודל הסטנדרטי.
עוד בנושא באתר הידען:

149 תגובות
הלֶמָּה של פֶרְמָפְרׂוסט (Permafrost's Lemma) :
הבה נתבונן בקבוצת מעגלים במשור אויקלידי בעלי נקודת מרכז משותפת ובזוית מרכזית משותפת אשר הישרים, קרניה, חותכים את כל המעגלים הללו.
אם המעגלים "מפוזרים" במשור ואינם בעלי מרכז משותף – נעתיקם תחילה אל נקודת מרכז משותפת שרירותית באמצעות מחוגה וסרגל(*).
קרני הזוית המשותפת חותכות סקטור או "פרוסה" מכל עיגול בן הקבוצה וקשת מכל מעגל בן הקבוצה.
כל ה"פרוסות" הללו דומות, אך נבדלות בפרמטר יחיד – הרדיוס.
ההבדל ביניהן הוא רק scaling.
עקב הדמיון, נובע מיידית שהיחס בין הקשתות השונות עליהן נשענת הזוית המרכזית המשותפת לבין רדיוסי המעגלים מהם נחתכו הקשתות הללו בהתאמה – קבוע.
יחס זה הוא, על פי הגדרתו, הזוית המרכזית, יהא גדלה אשר יהיה, והיא משותפת וזהה אצל כולם.
הרחבת הזוית המשותפת והכללתה לשעור של מלוא הזוית הנפרשׂת מנקודת המרכז גוררת כי היחס בין רדיוסי המעגלים לבין ההקפים המתאימים – קבוע, ולא משנה כלל מהו שעורו של קבוע זה.
(*) הסרגל – לשרטוט קוים ישרים בלבד. לא למדידה. אין סרגלי-מִדָּה מְשֻנָּתִים בגאומטריה.
לידען שלום.
יש לי הצעת יעול: חלוקת התגובות לתתי תגובות.
ואז
במידה ויש 2 גאונים (או יותר) שעושים את שנעשה בעמוז זה, אלו ירוכזו לעץ תגובות אחד.
מצב זה עשוי לאפשר הצגת דעות נוספות במקביל ל-2 גאונים (או יותר) המגיבים כאן.
https://en.m.wikipedia.org/wiki/Chronology_of_computation_of_%CF%80
חבל עאצבר , צריך עכשיו גם לשכתב את כל הערך הזה בויקיפדיה.
עצבר
שוב,
התאוריה שלך נשענת על שום דבר.
ההבדל בין החישובים שלך לחישובים המקובלים מעולם המתמטיקה והפיזיקה
הוא שהחישובים שלך מתייחסים אל דבר שלא קיים במציאות אלא קיים רק בראש שלך.
אתה מודד קוטר של גליל.
מה עם קוטר של פרוטון?
מדדת?
החישוב שלך נובע מתוך ניסוי שאינו לגיטימי.
אילו היית מבצע ניסוי לגיטימי היית נוכח בטעותך.
אתה כנראה לא מבין את המושג pi, אבל אתה בכל זאת ממשיך להפיץ את הדעות הלא קונבנציונליות והלא כדאיות שלך.
מסכן
(ראית את הסרט "Pi"? – אתה מזכיר את גיבור הסרט…)
aetzbar
התגובה הקודמת שלי הייתה מיועדת אליך.
כול תאוריה טובה נותנת ניבויים שאפשר לאמת אותם!
איזה ניבויים נותנת התאוריה שלך?
ציתות "נאסא צודקים, הם משתמשים בפאי מינימלי המתחיל עם הספרות 3.1415927 ,"
NASA לא משתמשת בפאי שכתבת, פאי של NASA הוא 3.141592653589793
הוכחתי לך גם שב טורבינת גז שקוטר הציר שלה 18.5 מ"מ, כלומר רמת דיוק של עשיריות ה מ"מ
כשהחישוב נעשה עם פאי קבוע
1. הפאי שלך לא נכון לחישוב מסלולי חלליות של NASA
2, גם בקטרים קטנים למשל בתכנון ציר של מנוע סילון לפי רמת הדיוק ב מ"מ הפאי שלך לא נכון
הסכמנו ? על מה הסכמנו ?
בסרטון יש את הנוסחה המקשרת בין קוטר המעגל המוצג במספר של מילימטרים, לבין ערכו של פאי
הנוסחה טובה מקוטר של 0.001 מ"מ, לאינסוף מ"מ
https://youtu.be/u4Y_i5D7WFM
בבקשה – אל תאכילו את הטרול. הגאון מוילנה לא טרח לרשום את הטמפרטורה בה היצע את הניסוי שלו.
aetzbar
אז הסכמנו שבקטרים גדולים אין שינוי בפאי הקבוע
ומה לגבי טורבינת גז שקוטר הציר שלה 18.5 מ"מ כלומר רמת דיוק של עשיריות ה מ"מ
טורבינת גז יכולה להגיע לאלפי סיבובים בדקה ולכן הקוטר המדויק של הציר חשוב
https://www.jvejournals.com/article/18765
לגל
נאסא צודקים, הם משתמשים בפאי מינימלי המתחיל עם הספרות 3.1415927 , מכיוון שפאי מינימלי מתאים למסלולי חלליות (קוטרים גדולים) , פאי מקסימלי שייך לקוטר המתקרב לאפס מ"מ, וערכו
3.164 בקירוב.
באמת, נו באמת, מה אתה רוצה מעצבר שלנו?
הוא הצליח להוכיח באמצעות ניסוי שפאי זהה בכל מעגל בתחום שגיאת המדידה, ועל זה מגיע לו כבוד והוקרה.
aetzbar
אתה חוזר כמו תקליט מקולקל, ולא עונה על השאלות.
הבאתי את NASA כדוגמה לחישוב מסלולי חלליות עם PI של 15 ספרות אחרי הנקודה 3.141592653589793
וזה סותר את התאוריה שלך, מה יש לך לומר?
בנוסף איזה ניבויים התאוריה שלך היא נותנת?
דע לך …באמת…כל הסיפור התחיל מדקארט
הגיאומטריה של דקארט
עיכבה את הופעת הגיאומטריה הפיזיקלית.
בגיאומטריה של דקארט יש כלי עזר , והוא מישור ממשי שעליו מצוירת נקודה , המסומנת באפס. נקודה זו משותפת להתחלה של שני קווי סרגל המצוירים במישור הזה , קו סרגל אופקי, וקו סרגל אנכי.
על גבי כלי עזר זה אפשר לסמן נקודות שמקומן נקבע על פי מספר סרגל אופקי , ומספר סרגל אנכי.
את המספרים של הנקודות מפיקה נוסחה כמו לדוגמה y=xx
אם נביט מרחוק באוסף נקודות צפופות של נוסחה זו, בקלות אפשר יהיה לטעות ולחשוב שמדובר בקו עקום, ולא באוסף של נקודות.
היות ומדובר באוסף של נקודות ולא בקו עקום, השם המתאים לאוסף נקודות כזה , הוא נקדן עקום.
בגיאומטריה של דקארט אין קווים, ובמקומם יש נקדנים.
כשהופיעה הגיאומטריה של דקארט, כבר לא היה צורך לצייר קו בעזרת עיפרון, והיה מספיק להשתמש בנוסחה המפיקה נקודות.
בגיאומטריה של דקארט אין קו עגול סגור הנוצר בעזרת מחוגה, ובמקומו יש נקדן עגול הנוצר מהנוסחה xx+yy=1
יש הבדל תהומי בין קו עגול סגור לנקדן עגול. לקו עגול סגור יש אורך ממשי כמו לדוגמה 45 ס"מ, וצורה אחידה ייחודית הנתפסת במבט פשוט.
ואילו לנקדן עגול אין אורך ממשי, ואין צורה.
אסור לצייר את נקודותיו של נקדן עגול, כי לנקודה מוחשית יש אורך ממשי, רוחב ממשי, וגם צורה. לנקדן עגול יש קיום רק במערכת הצירים של דקארט, עם נוסחה מתאימה.
בגיאומטריה של דקארט מושג הקו לא קיים, ובמקומו נמצא הנקדן.
הנקדן הוביל את הגיאומטריה אל קיפאון שעיכב את הופעת הגיאומטריה הפיזיקלית.
ניוטון ולייבניץ לא הרגישו בקיפאון זה, והם הציעו חשבון שאמור לטפל בקווים עקומים ועגולים.
חשבון זה כלל לא מטפל בקווים עקומים ועגולים, אלא בנקדנים עגולים ועקומים הנתפסים כקווים ישרשרים. (קו ישרשר בנוי מקטעי קו ישר)
לכל קו עגול סגור יש אורך ממשי וצורה אחידה ייחודית.
לכל קו עקום יש אורך ממשי, וצורה ייחודית
הנתונים האלה לא מופיעים בחשבון הניוטוני, ובמקומם מופיע קו ישרשר עגול, או קו ישרשר עקום.
התוצאה מהחלפת קו עגול בקו ישרשר עגול
הוא חשבון לא מדויק
החשבון הניוטוני יהיה בהכרח לא מדויק, ולכן הוא לא היה מסוגל לגלות את הקשר בין האורך הממשי של קו עגול סגור, למספר היחס בינו ובין
אורך הקוטר הישר.
את הקשר הזה גילתה הגיאומטריה הפיזיקלית
המתמטיקה צריכה לערוך ביקורת על כל פעילותה בתחום הגיאומטרי הרציף, על רעיון השאיפה לאפס ולאינסוף, על תוקפו של החשבון הניוטוני, על הכישלון בטיפול קווים שאינם ישרים, על המושג היסודי של הגיאומטריה, והגיע הזמן להבדיל בין גיאומטריה מתמטית המסוגלת לטפל בקטעי קו ישר, לבין גיאומטריה פיזיקלית המסוגלת לטפל בקווים עגולים ועקומים.
א.עצבר 1/4/2021
זה משתנה לפי מצב הרוח של התוקפים. היום למשל 24.
אחרי 150 תגובות, הבנתי את הלקות הספציפית שאעצבר סובל ממנה,
זה נקרא אינטגרל…
תגיד אדון אעצבר, אתה יודע מה זה אינטגרל ? שמעת כל המושג ? מענין שאין כל איזכור או חישוב של אינטגרלים בבבל"ת שאתה מנסה מקדם כאן. מהמעט שאתה יודע על אינטגרלים… אתה מבין שיש להם קשר לתאורייה ההזויה שאתה מנסה לשווק כאן ?
או שכל מושג האינטגרלים זה גם קשקוש שגוי ולא רלוונטי ? רק רוצה להבין מאיזה נקודה והלאה אני צריך לזנוח את התאורייה המדעית/מתמטית הקונבנציונלית ולעבור ליקום העאצברי ?
אבי ב.
אני מבין שהמערכת האוטונומית מכילה הרבה תגובות…
מהי כמות התגובות שמגיעות לאתר ביום?
אם זה לא סוד כמובן… תודה.
https://youtu.be/gX7-XyMVnSM
לידיעת אבי בליזובסקי הודעה זו לא נמסרה על ידי ,
aetzbar הגיב:
22 באפריל 2021 בשעה 17:27
אין צורך בניסוי. אין צורך בהוכחה. כל אדם יכול לראות בידיעה טבעית שקו עגול לא מתאים לחישובים.
האקדמיה יוצאת נגדי בגלל שהקדישו הרבה שנות לימוד על טעויות והם לא יודו בזה בחיים
שבת שלום, עצבר.
בטוח שעוד נשמע ממך רבות..
אין צורך בניסוי. אין צורך בהוכחה. כל אדם יכול לראות בידיעה טבעית שקו עגול לא מתאים לחישובים.
האקדמיה יוצאת נגדי בגלל שהקדישו הרבה שנות לימוד על טעויות והם לא יודו בזה בחיים
יפה, לך יש הוכחה של פאי קבוע, לי יש הוכחה של פאי משתנה , והכל בא על מקומו בשלום.
ענה על השאלה שנשאלת, עצבריהו.
ההוכחה היא בשבילך בלבד, חוץ ממך אף אחד לא מאמין בפאי משתנה..
ישראל , פרסם את ההוכחה שלך ,אם אתה בטוח שהיא ראויה לפרסום
aetzbar
NASA משתמשת ב PI עם 15 ספרות אחרי הנקודה 3.141592653589793
לשלוח חלליות.
האם לדעתך NASA טועה?
https://www.jpl.nasa.gov/edu/news/2016/3/16/how-many-decimals-of-pi-do-we-really-need/
גם האחרונה הומתנה..
גם זו תומתן..
העיקר הבריאות.
שתהיה בריא, אבי.
התגובות מומתנות כמעט תמיד..
ומה עם תגובות אחרונות?
יש מערכת אוטונומית ואני לא יכול להכנס כל שתי דקות לבדוק אותה. אתמול למשל לא הרגשתי טוב.
אבי בליזובסקי, למה כל ההודעות ממתינות?
אני לא נגד חיסונים! אפילו התחסנתי נגד קורונה! למרות שחליתי בקורונה!
אז למה התגובות מומתנות?
שלא לדבר כבר על למה אין תגובות אחרונות?
לא מצאתי הוכחות בעצמי, אך ההוכחה שהבאת דומה לשלי. תראה זאת אם תענה סופסוף על מה ששאלתי:
אינך מקבל שיש יחס מסויים בין מיתר לקשת בין אם אתה יכול לחשב אותו או לא?
יש הרבה הוכחות לפאי קבוע, הנה אחת מהן
https://math.wikia.org/wiki/Proof:_Pi_is_Constant
זה הזמן לפרסם את ההוכחה שלך
הוכחה 1:
ברור לכל מי שעיניו בראשו ויש לו יושרה מינימלית שה"PI המשתנה" בעצם שואף לPI. אפשר לראות בין השורות שזה אפילו המסקנות של עצבר. (למשל מה שהוא כתב על מעגל קטן עם הזמן). רק שסתירה פנימית זה לא מה שיעצור טרול טרחן כפייתי
הוכחה 2:
נוכחות של שורש בנוסחא שלו סותרת את כל מה שהוא מנסה להגיד. ברור שגם פה הוא בחר להתעלם.
עובדה מרכזית היא שטרחנים כפייתיים פשוט מתעלמים מכל מה שסותר את דעתם.
אגב משעשע לראות שעצבר מדגים כמעט את כל התכונות בהגדרה של טרחנים כפייתיים 🙂
טט״כ
איזו הוכחות הובאו לעצבר שמראות שהוא טועה על פי המתמטיקה שלו?
זה נראה טריוויאלי שפאי זהה לכל מעגל, אך לא מצאתי לכך הוכחה ברשת. אני מאמין שהצלחתי למצוא אחת כזו, וזו תכלית הדיון.
יש גם ערך נוסף – אני מתחיל להבין שמה שגורם לאנשים ליצור תילי תילים של תאוריות הזויות הוא פשוט שהם – איך נאמר בעדינות – קצת מאותגרים..
ראה כמה זמן עצבר נלחם על להבין שגם אם הוא אינו מסוגל לחשב אורך קשת לפי מיתר (פעולה טריוויאלית בגאומטריה אוקלידית) אין זאת אומרת שיחס כזה אינו קיים..
מה יהיה אליהו? לא ברור לך שלא תקבל תשובות? שברגע שעצבר יגיע לסתירה (הראו לו 2) הוא יענה על הכל מלבד מה שרלבנטי? לא הוכח מעבר לכל ספק אפשרי שהוא טרול+טרחן כפייתי? שהוכחות לא משנות לו כלום?
אני כבר מתחיל לתהות מה *אתה* מנסה להשיג, ולמה אתה חושב שתשיג את זה
מה יהיה עצבר?
אינך מקבל שיש יחס מסויים בין מיתר לקשת בין אם אתה יכול לחשב אותו או לא?
ישראל, במקום לשאול שאלות שבשבילי הן מלל חסר פשר, אני מציע שתכתוב את "התיאוריה הישראלית" על קשת עגולה והמיתר הישר שלה , ותפרסם אותה כאן.
אין ספק שתקבל הרבה תגובות.
התיאוריה העצברית אומרת : אי אפשר לחשב את אורכה של קשת עגולה על פי אורך המיתר הישר שלה.
ננסה בשלבים.
יש מעגל שקוטרו 0.01 מ״מ.
במעגל יש מיתר שאורכו מיליארדית המ״מ.
שאלות:
1. האם אתה מקבל שקיים יחס מסויים וקבוע בין אורך המיתר לאורך הקשת שלו, בין אם ניתן לחשב אותו או לא?
2. האם אתה מקבל שאותו יחס קיים בין כל מיתר אחר שאורכו מיליארדית המ״מ לקשת שלו, באותו המעגל או בכל מעגל אחר בקוטר 0.01 מ״מ?
הכוונה היא שאם היחס הוא x אז בכל מעגל בקוטר 0.01 מ״מ נקבל תמיד את אותו היחס x בין אורך מיתר באורך מיליארדית המ״מ לקשת שלו (לדוגמה 0.999,99965) בין אם נוכל לחשב את אותו היחס או לא – הוא עדיין קיים ונשאר קבוע.
מקבל?
לישראל
אולי מה שיש בוויקיפדיה יתאים לך
https://he.wikipedia.org/wiki/%D7%94%D7%92%D7%91%D7%95%D7%9C_%D7%A9%D7%9C_sin(x)/x
אני אשתדל לנסח את מה שהבנתי משאלתך,בצורה פשוטה ומובנת.
נתון מיתר במעגל, ואורך המיתר הזה הולך וקטן עם הזמן בכיוון אפס מ"מ
יש רגע שאורכו 1 מ"מ, ורגע שאורכו 0.1 מ"מ, ורגע שאורכו 0.0001 מ"מ, וכך הלאה לנצח.
ברור ומובן מאליו שגם אורך הקשת העגולה שלו, הולך וקטן בכיוון אפס מ"מ
אם המיתר הזה נמצא במעגל גדול אז מספר המעבר בין אורך המיתר לאורך הקשת, יהיה תמיד גדול מ 1 והוא משתנה תמיד לכיוון 1 (אי אפשר לחשב את המספר הזה)
ואם המיתר הזה נמצא במעגל זעיר, אז מספר המעבר בין אורך המיתר לאורך הקשת, יהיה תמיד גדול מ 1 והוא משתנה תמיד לכיוון 1 (אי אפשר לחשב את המספר הזה)
אני הבנתי משאלתך שאתה מצפה לתשובה במספרים, אבל אין כזו.
אתה יכול להחליט סתם כך, שאחרי אינסוף שנים, מספרי המעבר יהיו 1, אבל את ההחלטה השגויה הזו עשו כבר לפניך מתמטיקאים מפורסמים.
אתה מתחמק, כמו תמיד.
לא בקשתי את הגודל המדוייק, ביקשתי תחום. גם אתה מרבה לדבר על אי שוויונים, כל רעיון הפאי המשתנה שלך אינו נותן פאי מדוייק אלא תחום מסויים.
אז כמה בערך, עצבר? בין 1.007 ל1.008? זה הרי לא יכול להיות תחום גדול מדי, מה היחס בין הקשת למיתר שאורכו מיליארדית המ״מ?
אתה לא תיתן תשובה, אפילו לא בערך. אבל אתה יודע היטב שזו מכת המוות לגאומטריה שלך:
אם היחס גדול יחסית – זה סותר את אקסיומת המרחק הקצר בין 2 נקודות.
קטן – אז לכל המעגלים פאי זהה.
אז כמה בערך, עצבר?
ישראל, אתה כבר צריך לדעת שעל השאלה ששאלת 7 פעמים אין תשובה,
יש כלל האומר: – אי אפשר לחשב את אורכה של קשת עגולה, על פי אורך המיתר הישר שלה.
ולכן, לעולם אין לדעת פי כמה ארוכה הקשת מהמשיק שלה.
פי כמה פירושו מספר, ואת המספר הזה אי אפשר לחשב.
הנה קטע של מאמר שפרסמתי
הדרך היחידה שבה ניתן להשיג את מספר המעבר בין אורך מיתר המופיע במעגל , אל אורך הקשת העגולה שלו, היא על ידי מדידת אורך המיתר , והערכת אורך הקשת.
שים לב: מדובר על מדידה עם סרגל, והערכה על פי מבט.
מכל צירוף של מדידה והערכה, מושג מספר מעבר שבהכרח אינו מדויק.
דוגמה: במעגל נתון נמדד מיתר באורך 32 מ"מ, ואורך קשתו הוערכה ב 38 מ"מ.
מספר המעבר הלא מדויק בין אורך המיתר לאורך הקשת הוא 1.1875
עוד דוגמה
במעגל נתון נמדד מיתר באורך של 8 מ"מ , וקשה מאוד להעריך את אורך הקשת שלו, כיוון שזה מעגל גדול מאוד. על כן הערכתי את אורך הקשת ב 8.05 מ"מ , כאשר ברור לי הערכה זו אינה מדויקת.
מספר המעבר הלא מדויק בין אורך המיתר לאורך הקשת העגולה שלו הוא 1.00625
ומה בטוח בהערכה זו ? שאורך הקשת גדול מאורך המיתר שלה
לכן,
אין טעם שתחזור שוב ושוב על אותה שאלה, ואין טעם לכל החישובים , המנסים להשיג את מספר המעבר בין קוטר המעגל להיקפו.
קוטר המעגל הוא המיתר הגדול ביותר, וההיקף הוא 2 פעמים הקשת העגולה שלו, והכלל הרי אומר.
אי אפשר לחשב את אורכה של קשת עגולה, על פי אורך המיתר הישר שלה.
אולי בעולם המושגים הפרטיים שלך. באקדמיה – שאת הכרתה אתה מבקש באופן כה נואש – מספר רציונלי הוא מספר שניתן להציגו כחלוקה של שני מספרים שלמים.
״מאכסיומה זו נובע, שקשת עגולה, תמיד ארוכה יותר מהמיתר שלה״.
אבל פי כמה עצבר, פי כמה? מה הוא היחס המינימלי (שאלתי רק 7 פעמים).
אם הוא גדול – ו1.007 אינו יחס זניח כלל – אז ניתן לבנות בתוך הקשת משולש שבו סכום הצלעות הנגדיות שוות לבסיס.
אם הוא קטן, אז אורך המצולע שמתקבל מחיבור כל המיתרים שווה כמעט בדיוק לאורך המעגל, ולכן ניתן להראות בקלות שפאי זהה לכל מעגל.
אז פי כמה?
אתה כמובן לא תענה כי זו תהייה מכת מוות לכל הגאומטריה שלך. בכל אופן, עזרת גם בתאוריה וגם בניסוי להראות שפאי זהה בכל מעגל ועל כך מגיעה לך כוכבית. כפיים לעצבר!
לישראל,
קודם כל יש לתקן טעות הקלדה בהודעתי הקודמת
צריך להיות
אמור מעתה: 1 הוא המספר האי רציונלי היחידי, וכל שאר המספרים והאנטי מספרים הם רציונליים.
והיה רשום
אמור מעתה: 1 הוא המספר האי רציונלי היחידי, וכל שאר המספרים והאנטי מספרים הם אי רציונליים.
ברור שמקובלת עלי האכסיומה של המרחק הכי קצר, וכך אני תופס אותה
למרחק הכי קצר בין שני מקומות יש צורה אחידה ייחודית שאפשר להמחישה עם שרוך מתוח.
את הצורה הזו תופסים במבט פשוט, והשם המוסכם שלה הוא צורת קו ישר.
את כל הגיאומטריה האוקלידית אפשר לבסס על אכסיומה זו, ואין צורך ב5 אכסיומות, וכמובן שאין צורך ב 21 אכסיומות.
מאכסיומה זו נובע, שקשת עגולה, תמיד ארוכה יותר מהמיתר שלה.
אליהו קיבלת עוד הוכחה שעצבר טרול וטרחן כפייתי.
הוא קיבל *שתי* דוגמאות לסתירות פנימיות ונשאל עליהן 2 שאלות פשוטות.
תגובותיו:
1. התעלמות מהסתירה ואי התייחסות לטענות/שאלות (בגלל חוסר יושרה כנראה)
2. חזרה לטרמינולוגיה מומצאת שרק הוא מכיר
האלטר אגו "דוקטור תומר" דווקא לא חזר ולא הזדהה…
כמובן, כמובן.. המצאת כבר את כל ההגדרות והאקסיומות מחדש, אז למה לא את הגדרת המספרים הרציונלים?
מה עם האקסיומה שאומרת שבין שתי נקודות עובר רק קו ישר אחד שהוא גם המרחק הקצר ביותר ביניהן, אותה אתה מקבל? כי אם כן הלכה לך כל הגיאומטריה העצברית המפוארת ותוכל לראות זאת אם תענה סופסוף על השאלה: מה היחס המינימלי בין אורך קשת למיתר שלה במעגל ברדיוס 0.01 מ״מ.
רציונלי – יחסי
אי רציונלי – מוחלט
המצאת המספרים מבוססת על המצאת 1 וזה המספר היחידי המוחלט , וכל מה שאפשר להגיד עליו מופיע במשוואה 1=1
כל מספר אחר גדול מ 1 הוא מספר יחסי , והוא מובן על פי צבירת 1
כל אנטי מספר כמו לדוגמה אנטי 3 הוא מספר יחסי קטן מ 1 והוא מובן על פי חלוקת 1 ל 3 חלקים שווים, ושימוש בחלק יחיד מחלוקה זו.
אמור מעתה: 1 הוא המספר האי רציונלי היחידי, וכל שאר המספרים והאנטי מספרים הם אי רציונליים.
זה מה שיש בכמתנות 1 , מספרים גדולים מ 1 , ומספרים קטנים מ 1 המכונים אנטי מספרים.
המספרפרים הופיעו בעקבות תהליך של מדידה ממשית, ויש להם שימוש בתחום הגיאומטרי הרציף, בעקבות הפגם היסודי של המצאת האנטי מספרים.
http://img2.timg.co.il/forums/3/45317ede-eca8-48bc-8608-477e5a47c910.pdf
הביטוי ״מספר רציונלי״ מגיע מהמילה ratio – יחס, חלוקה, ומשמעותו מספר שניתן להציגו כחלוקה של שני מספרים שלמים.
…..1.666666 הוא מספר רציונלי כי הוא חלוקה של 5 ב3
0.4 הוא מספר רציונלי כי חלוקה של 2 ב5.
שורש 2 אינו מספר רציונלי כי אין שני מספרים שלמים שניתן לחלקם זה בזה כדי להגיע איליו.
מה עם היחס בין אורך קשת למיתר, עצבר? 1.007 אינו יכול להיות היחס הקטן ביותר כי הוא מאפשר בניית משולש שבו סכום 2 צלעות שווה לשלישית.
מספר קטן בהרבה עד כמעט שוויון בין שני המספרים סותר מיד את פאי המשתנה. (הסבר למי שמעוניין).
אז מה המספר, עצבר? מה אומרים הידיעה הטבעית או הכלל הבטוח בנידון?
אצבר אתה מתחמק מהשאלה.
אם מציבים ב"נוסחא" המומצאת שלך 3 איזה תוצאה היא נותנת? מספר לא קיים לפי ההגדרות *שלך* ומה לגבי להציב 5? 7?
ה"נוסחא" שלך קורסת עבור אינסוף דוגמאות.
אתה יכול להמציא שמות עד מחר אבל עשית טעות קטלנית.
מרגע שהשתמשת בשורש המון תוצאות נותנות מספרים שאין להם משמעות לפי ההגדרה *שלך*
מה התשובה שלך לזה? פרפרים? מספרפרפרפרים? טרולים?
עשית טעות טפשית ואתה פחדן מדי להתייחס ובטח שלא להודות.
בכל פעם שתכתוב משהו זאת התגובה שהקוראים יקבלו
לקטעים איתך
אני לא יודע אם אי פעם הקהילה המדעית תסכים אתי, אבל אני יודע שהמציאות הפיזיקלית הסכימה אתי.
ניסוי ההיקפן שאל את המציאות הפיזיקלית שאלה ברורה – פאי של קוטר 2 מ"מ ( שווה או לא שווה) לפאי של קוטר 120 מ"מ ? והמציאות הפיזיקלית השיבה .." לא שווה"
ואם המציאות הפיזיקלית הסכימה אתי, הקהילה המדעית חייבת לקבל את פסיקת המציאות הזו.
אבל
זה מאוד מובן שהמתמטיקה פוסלת את ניסוי ההיקפן, מכיוון שהיא לא מסכימה , שניסוי מכני פשוט
(אבל מדויק) יכול לגלות אמת מתמטית, שהמתמטיקה בכלל לא מסוגלת לגלות.
2000 שנים נמסר מדור לדור הרעיון המתמטי השגוי של פאי קבוע, וצריך רק להמתיו למתמטיקאי נועז מהאקדמיה, שיקום ויכריז….טעינו.
למשתתף שדיבר על מספר אי רציונלי
מספר אי ארציונלי הוא מספר מוחלט שערכו נודע מעצמו, ולא ממספר אחר.
לכן, 1 הוא המספר האי רציונלי היחידי , כיוון שערכו נודע מתוך עצמו על המשוואה 1 = 1
לעומת זאת, 3 הוא מספר רציונלי (כלומר יחסי )שערכו נודע מתוך צבירת 1 ועוד 1 ועוד 1
אמור מעתה: 1 הוא המספר האי רציונלי היחידי, (או המוחלט היחידי) ,וכל שאר המספרים הם רציונליים.
(כלומר יחסיים)
מה נשאר ? העיקר כמובן – כל מדידה מסתיימת במספרפר ולעולם אינה מסתיימת במספר.
המספרפר שייך למתמטיקה העצברית, ששמה העברי המתאים הוא כמתנות.
http://img2.timg.co.il/forums/3/45317ede-eca8-48bc-8608-477e5a47c910.pdf
אז אתה טוען שבעיגול בעל קוטר 0.001 מ״מ היחס המינימלי בין אורך קשת למיתר שלה הוא 1.007? מה עם המיתר הוא באורך מיליארדית המ״מ? מה עם מיתר בעל אורך מיליארדית המיליארדית? עדיין היחס לא קטן מ1.007?
היחס "אורך קשת זעירה חלקי אורך מיתר זעיר" תמיד גדול מ 1 , היות וקשת תמיד ארוכה יותר מהמיתר שלה.
ואולם, יחס זה הולך ומתקרב ל 1, כאשר מדובר מדובר בקשת השייכת למעגל ענק, שקטע זעיר מקו ההיקף שלו, "נראה כמעט כמו קו ישר.
כאשר מדובר במעגל זעיר שקוטרו לדוגמה 0.01 מ"מ, היחס הזה ילך ויתקרב ל 1.007
http://img2.timg.co.il/forums/3/feaa8e28-ae7a-4966-b3c1-c4d37108da00.pdf
ההתקרבות ליחס של 1.007 שייכת לגיאומטריה העצברית שבה פאי משתנה
1.007 מביע את היחס בין פאי מקסימלי לפאי מינימלי
נו באמת עצבר..
כאשר המיתר הוא הקוטר, היחס בין אורך הקשת שלו (חצי המעגל) למיתר גדול מ1.5. על זה כולנו מסכימים, נכון?
כשהמיתר באורך הרדיוס, היחס קטן יותר, לא?
כשהמיתר מאית מהרדיוס, הוא קטן עוד יותר, נכון?
וכשהוא מיליארדית הוא קטן עוד, מסכימים?
וכשהמיתר ממש קטן, קטנטן, איצי ביצי, גוז׳ון – האינך רואה שהוא הולך ושואף לאורך הקשת שלו?
זו אגב הדרך המתמטית שבה חישבו פעם את פאי: סכמו את אורך כל בסיסי המשולשים שנוצרו עיי מיתרים קטנים והולכים עם אורך הרדיוס כשתי הצלעות הנוספות.
אז מדוע שלא תגיע ליחס קשת/מיתר של 1.000,000,001 או אפילו קטן יותר? אין לכך מניעה בגיאומטריה האוקלידית, אבל מה עם העצברית?
השאלה ששאלת אינה מובנת לנשאל , ואני משער שגם אינה מובנת לשואל
אם תסכים לקבל את כלל א (שממנו נובע כלל ב) , השאלה שלך תהפוך להיות מלל חסר פשר.
א. אין למתמטיקה יכולת לחשב את אורכה של קשת עגולה , על פי אורך המיתר הישר שלה.
ב היות והמיתר הארוך ביותר של מעגל הוא הקוטר, והיות שהקשת העגולה שלו היא מחצית היקף המעגל, אז אין למתמטיקה יכולת לחשב את היקף המעגל על פי קוטרו.
בקיצור, המעגלים לא שייכים למתמטיקה , והטיפול בהם אפשרי רק בדרך פיזיקלית של מדידה.
שוב חזרנו אל הגיאומטריה העצברית, שבהחלט ראויה לשם גיאומטריה פיזיקלית.
איזה פחדן אתה עצבר!
מסרב להתעמת עם השאלה הפשוטה למה יש שורש בנוסחא שלך, בנוסחא *פיסיקלית* בגיאומטריה *פיסיקלית*.
שורש נותן לרוב מספר לא רציונאלי שאי אפשר למדוד? בתיאוריה שבנויה על זה שאין מספרים כאלה?
מה קרה? קרסה לך התיאוריה ואתה מפחד להתעמת עם המציאות?
נתקלת בטיעון שגדול עליך והשתפנת?
סתם מתוך סקרנות אעצבר, מעבר לכל דיוני הסרק, על היקום האעצברי המהולל… וחריטת גלילים..
מה ההסתברות ,לדעתך, שהתאוריה המהפכנית שלך תזכה אי פעם לאיזה שהיא הסכמה ופופולריות על ידי איזה שהוא קונצנזוס מדעי ? נראה לך אפשרי ? אוטוטו ?
אני חייב להודות שזה לא נראה מבטיח במיוחד, אם לשפוט לפי התגובות כאן ? אולי כדאי להעזר בשירותי יחצנ"ות ?
אי אפשר להיות מושלם בכל התחומים..
תן למקצוענים לעשות את העבודה..
אבל לא ביקשתי לחשב אורך קשת עגולה על פי אורך המיתר הישר שלה, ביקשתי לדעת אם יש מיתר שהיחס בין ההבדל בין אורכו לאורך הקשת גדול ממיליארד..
הרי יש יחס כזה, בין אם חישבנו אותו או לא, לא?
ומדוע שלא יהיה מיתר כזה אם ניקח מיתרים קטנים ככל שנרצה? זו הרי בדיוק הדרך שבה חישבו את פאי, עיי מיתרים קטנים יותר ויותר. האם יש הגבלה בגיאומטריה העצברית על קוטן המיתר?
אין תשובה לשאלה שלך , מכיוון שאי אפשר לחשב אורך קשת עגולה, על פי אורך המיתר הישר שלה
ואם אי אפשר לחשב אורך קשת עגולה על פי אורך המיתר הישר שלה, אז אי אפשר להשיג את "מספר המעבר" מאורך מיתר אל אורך הקשת העגולה שלו.
הדרך היחידה שבה ניתן להשיג את מספר המעבר בין אורך מיתר המופיע במעגל , אל אורך הקשת העגולה שלו, היא על ידי "מדידת אורך המיתר" , "והערכת אורך הקשת".
מכל צירוף של "מדידה והערכה", מושג מספר מעבר שבהכרח אינו מדויק.
כנראה שלא הייתי ברור מספיק, אז הנה השאלה לעצבר פעם נוספת:
האם אתה מקבל שבמעגל קטן – נאמר קוטר 1 ס״מ – ניתן למתוח מיתר שההבדל בין היחס של אורכו לאורך הקשת שלו קטן מ1 למיליארד? או אפילו 1 לטריליון?
אם לא, מהו היחס המקסימלי?
אנסה פעם נוספת, אולי עצבר יתפנה מעיסוקיו בעינייני ד׳מעלה ויענה:
האם קיים מיתר במעגל של רדיוס ס״מ שההבדל בינו לקשת שלו פחות מ1 למיליארד? אם לא, מה ההבדל המקסימלי?
http://img2.timg.co.il/forums/3/447ba886-c89e-42a7-bfb4-8d2c9be59c73.pdf
עצבר הנוסחא שלך שגויה ע"פ ההגדרות של עצמך. שורש יתן מספר לא רציונאלי לרוב הרדיוסים, ומספר לא רציונאלי לא קיים לפי ההגדרות שלך כי אין בעולם הפיסיקלי גודל מדיד לא רציונאלי.
מזל טוב, עשית לעצמך מט שאתה לא מספיק ישר כדי להודות בו
מה שתגיד עצבר, מה שתגיד.
אתה הרי קובע את החוקים ואת האקסיומות, אז למה שלא תקבע גם מהי שגיאת מדידה?
מה עם השאלה שלי? האם קיים מיתר במעגל של רדיוס ס״מ שההבדל בינו לקשת שלו פחות מ1 למיליארד? אם לא, מה ההבדל המקסימלי?
"את זה יכול לעשות רק נציג האקדמיה של המדעים המדויקים, כשהתוצאה הבלתי נמנעת היא דרמה מדעית מנפצת מוסכמות"
תכף אני מתקשר ל "נציג האקדמיה של המדעים המדויקים" . באמת לא בסדר.
לא הייתי מודע…יש להם נציג ? במיוחד למיקרים כאלו ?
זו התחלת תגובתך האחרונה והיא אומרת כך
ישראל שפירא הגיב:
18 באפריל 2021 בשעה 22:58
אכן ערכת ניסוי שהראה שיחס הפאי בין 2 גלילים בקטרים שונים בהרבה הוא 1 בתחום שגיאת המדידה.
ובכן , מה שכתבת אינו נכון
הניסוי שערכתי הראה שיחס הקטרים של שני גלילים (גדול במעט) מיחס ההיקפים שלהם.
ההפרש הוא זעיר, אבל וודאי ונמצא מעבר לתחום השגיאה.
להפרש הזעיר הזה יש משמעות עצומה, כיוון שהוא אומר שפאי של הגליל הקטן, גדול במעט מפאי של הגליל הגדול.
ואם תשאל…כמה זה גדול במעט ? כנס אל הסרטון ביוטיוב The pi revolution ויש שם נוסחה המסוגלת לחשב את פאי של קוטר 2 מ"מ, ואת פאי של קוטר 120 מ"מ.
אכן ערכת ניסוי שהראה שיחס הפאי בין 2 גלילים בקטרים שונים בהרבה הוא 1 בתחום שגיאת המדידה.
והרשה לי להטיל ספק באינטגריטי או אפילו השפיות של אדם שטוען שהוא צודק נקודה, ואין צורך לערוך ניסוי שיוכיח את צדקתו.
אך נעבור לתחום התאורטי. האם אתה מקבל שבמעגל קטן – נאמר קוטר 1 ס״מ – ניתן למתוח מיתר שהבדל בין היחס של אורכו לאורך הקשת שלו קטן מ1 למיליארד? או אפילו 1 לטריליון?
אם לא, מהו היחס המקסימלי?
אין צורך בניסוי, כבר הסברתי לך שוב ושוב.
הניסוי יכול ליצור דרמה מדעית מזעזעת מוסכמות בנות 2000 שנים, ובתנאי שיבצע אותו נציג האקדמיה של המדעים המדויקים.
אני ערכתי את הניסוי, ושום דרמה לא נוצרה, ובמקומה הופיעה כצפוי פסילה מוחלטת של הניסוי.
אני יודע כי אין צורך בניסוי, וכל בר דמיון ודעת, יכול לדעת כי פאי אינו קבוע בכל המעגלים, אלא הוא משתנה בתחום מספרי צר שכבר הצגתי אותו.
התיאוריה של פאי המשתנה הייתה קיימת אצלי עוד לפני המצאת ההיקפן, והניסוי שערכתי נועד
להוכיח לי שהתיאוריה נכונה , ואכן הוא עשה זאת.
עכשיו צריך להוכיח את התיאוריה לקהילה המדעית העולמית, ואת זה יכול לעשות רק נציג האקדמיה של המדעים המדויקים, כשהתוצאה הבלתי נמנעת היא דרמה מדעית מנפצת מוסכמות .
אז אני מציע לך להירגע, ולחכות בסבלנות עד שנציג האקדמיה ירגיש צורך להופיע, ולהגן על הרעיון של פאי קבוע, שקיים מזמן ארכימדס.
אם הניסוי כל כך חשוב לך ארגן קבוצת תמיכה שתפנה אל הטכניון בדרישה לחזור על ניסוי ההיקפן.
האם הטכניון יסכים ? אני לא יודע, אבל אם הדיון הזה יובא לידיעתו, יתכן שכן יסכים.
ואם הוא יסכים , זו תהיה ההצגה המדעית הגדולה של המאה ה 21, שתיצור שינוי פרדיגמה במתמטיקה, בגיאומטריה, ובפיזיקה.
יאללה עצבר חלס חרטט, על מי אתה חושב שאתה עובד?
בן אדם מבוגר שמשחק בקקה, אין לך טיפת כבוד?
לך כבר תבצע את הניסוי נודניק. את מי חוץ ממך מעניינת הדרמה, אתה לא מבין שבלי עובדות מוצקות אף אחד לא יתיחס אליך ברצינות וכולם פה רק נהנים להסתלבט עליך? זה התפקיד שבחרת לעצמך?
בצע כבר את הניסוי או שתבין את מקומך האמיתי: שוטה הכפר.
ישראל, יש חוק ידוע "כאשר הוויכוח גולש מהעניין הנדון עצמו, למצבו הפסיכולוגי של בעל העניין,
סימן הוא שבעל העניין צודק."
אתה בדרך כלל מדבר לעניין, אך לא כל המשתתפים בדיון זה הם כאלה.
ואפילו בתגובתך זו דיברת לעניין, כאשר הבאת ניסוי שבו מקרינים על הקיר, תמונה של קו עגול סגור
המצויר על שקף, שאורכו לדוגמה 7 ס"מ , ומקבלים על הקיר תמונה של קו עגול סגור שאורכו לדוגמה 140 ס"מ
לכל קו עגול סגור יש שני נתונים ברורים , צורה אחידה ייחודית, ואורך ממשי.
לקו המצויר על השקף יש אורך ממשי של 7 ס"מ, ויש לו צורה אחידה מסוימת.
לקו העגול סגור המופיע על הקיר, יש אורך ממשי של 140 ס"מ, וצורה אחידה שהיא שונה מהמסוימת.
עם דוגמה זו אתה מביע תמיכה של ממש בגיאומטריה העצברית.
יש אינסוף קווים עגולים סגורים בכל אורך ממשי שנרצה, ולכל אורך ממשי יש צורה אחידה ייחודית.
והיות שהביטוי המתמטי של צורה הוא תמיד מספר יחס,
והיות שהאורך הממשי של קו עגול סגור קובע בהכרח את האורך הממשי של קו הקוטר הישר שלו,
אז היחס בין אורכו הממשי של קו עגול סגור לאורכו הממשי של קו הקוטר שלו, מביע את הצורה האחידה ייחודית של הקו העגול סגור.
תודה רבה על תמיכה בלתי צפויה זו,
הסיכום שלי מן הדיון הוא יותר פסיכולוגי מטכנולוגי.
נכנסתי לדיון עם הפסקה הבאה:
״אליהו וכולם, שימו לב שלפני עצבר עומדות כעת 3 אפשרויות, עם 3 תוצאות אפשריות:
1. עצבר יבצע את הניסוי עם 100 סיבובים (לא יותר משעה) או עם 10 סיבובים (10 דקות), יפרסם את הוידאו, ויוכיח לעולם את צדקתו. גאון!
2. הוא יבצע את הניסוי יווכח בטעות ויודה בה. קראקפוט, אבל ישר.
3. הוא יסרב לבצע את הניסוי ויאמר שהניסוי שביצע כבר מספיק. שרלטן״.
מדיונים קודמים עם עצבר, היה לי ספק מועט שעצבר נופל לקטגוריה השלישית: שרלטן. אך התועלת שבדיון שהיה פה היא ההבנה למניעים של הטרחנים הכפייתיים, שעצבר חשף לפנינו באופן כה מרשים: בדידות, שיעמום, שגעון גדלות.
שהרי אילו עצבר היה באמת מאמין בטענות עצמו, הוא היה מקדיש את אותם
20 דקות ועורך את ניסוי ההיקפן בדרך נאותה. סירובו מעיד על כך שהוא יודע שהניסוי שלו פגום, וקריאתו ל״דרמה״, מראה את ערכו הפגום כמדען אובייקטיבי, חסר פניות.
ולעצם העניין: מעגלים קטנים אכן נראים קעורים יותר מגדולים, וכמותם אליפסות ומצולעים. ניסיתי בזמנו להראות לעצבר שזו אשליה אופטית, שאם נקרין שקף של עיגול ונציב מולו מסך במרחקים שונים נקבל מעגלים גדלים והולכים שכולם הם בעצם אותו עיגול יסודי שגדל בגלל הפרספקטיבה ולכן אין אפשרות שהיחס בין ההיקף לרדיוס ישתנה. ניסוי זה בא כדי להראות שטענתו להבדל בין המתמטיקה (שבה פאי מתקבל באופן אלגברי) לגיאומטריה, שגויה. עצבר סירב להתעמת עם טענה זו מעולם הפיזיקה והגאומטריה, כמו עם כל יתר הטענות.
ההערכה שלי היא שעצבר יודע כנראה שאין לטענתו לפאי משתנה כל בסיס, אך פשוט נהנה מכל ההמולה סביבו פשוט מכייוון שזו דרך התקשורת החברתית היחידה שהוא מכיר.
קריסה של הגיאומטריה של עצבר!
1. עצבר השתמש ב*שורש* בנוסחא. ידוע שאין גודל מדיד לשורש 2! עצבר מקדם סתירה פנימית בגיאוטרית עצבר שתעכב אותנו עשרות שנים!
2. עצבר קבע נוסחא ל0.1 מ"מ. הנוסחא חסרת משמעות למספרים קטנים יותר.
3. עצבר איבד אמון בניסוי של עצמו ולא מוכן לחזור עליו בדיוק רב יותר!
4. עצבר הוכיח שPI קבוע עד כדי שגיאת הניסוי (שהוא לא מבין מה זה)
5. עצבר הודה שההגדרה המתמטית לPI והחישוב שלה נכון
6. אה והוא טרול טרחן כפייתי שהודה שהכל למען הדרמה שאצלו בראש בלבד, ולא מבין מושגים בסיסיים שתלמיד תיכון מבין
תגובה זו תבוא אחרי כל קשקוש טרולי של עצבר
אני מציע לסיים את הרב שיח המעניין הזה, בסיכום קצר
עתה יש להבדיל בין גיאומטריה מתמטית לגיאומטריה פיזיקלית.
הגיאומטריה של הקו הישר היא מתמטית, וגולת הכותרת שלה הוא משפט פיתגורס.
הגיאומטריה של קווים עגולים סגורים (המכונים מעגלים) היא פיזיקלית, וגולת הכותרת שלה היא נוסחה המקשרת בין קוטר ממשי של מעגל , למספר המעבר שלו.
Transition number = 3.1416 + root of (0.0000003 : D above 0.001 mm)
אין כל קשר בין גיאומטריה מתמטית לגיאומטריה פיזיקלית, כמו שאין כל קשר בין קו ישר, לקו עגול סגור.
סיכום: קיימת במציאות גיאומטריה מתמטית מוכרת וידועה זה אלפי שנים,
וקיימת במציאות גיאומטריה פיזיקלית שניסוי ההיקפן גילה אותה לא מזמן.
aetzbar
אם המאמר שלך יופיע על טישו אז יש סיכויי שאמצא בו שימוש….
10 שנים, ועדיין לא מצאת 3 חודשים לעשות קורס בחשבון אינטיפיסמלי ?
מענין גם שאתה בוחר להתעלם מכך שאפשר לחשב את פיי מדוייק מסדרה אינסופית… טוב. אני מניח שזה דורש קצת הבנה בחשבון אינטיפיסמלי..
הנה מאמר שלי מלפני יותר מ 10 שנים, הנושא את השם "גיאומטריה עצברית"
יש בו את הרקע הפיזיקלי לפתרון חידת המעגלים, אבל עוד אין בו את המצאת ההיקפן.
http://img2.timg.co.il/forums/1_162255757.pdf
אל תתרגש מהביטו "גיאומטריה עצברית" אפשר להחליפו בביטוי "גיאומטריה פיזיקלית"
כאן בטח תתרגש יותר
שני המושגים היסודיים ביקום הניוטוני הם כוח וחומר
שני המושגים היסודיים ביקום האיינשטייני הם אנרגיה וחומר
ושני המושגים היסודיים ביקום העצברי, הם אנרגיה וזמן פסיבי.
הנה מאמר קצר המתאר את היקום העצברי
http://img2.timg.co.il/forums/2/ac193a50-8b58-4711-89bd-475f16879d2a.pdf
אגב, הערה כללית ..
בדרך כלל תאוריה נקראת על שם הממציא שלה , רק עלידי אנשים אחרים, ולא עלידי החוקר עצמו (לדוגמא, אני די בטוח שאיינשטיין לא התייחס לתורת הייחסות שלו כתאוריה של איינשטיין, או שהוקינג לא השתמש במושג קרינת הוקינג לתאור האפקט שלו.
מה עוד, שבדרך כלל גם נוהגים להשתמש בתאור הנל אחרי שהתאוריה הוכחה או לפחות זכתה לפופולריות גדולה מאפס.
הנ"ל אמור להדליק אצלך כמה נורות אזהרה בהקשר של שיגעון גדלות. ונכות חברתית . תנחומי.
אעצבר.
האם יש לך הסבר למה החישוב הנ"ל לא נכון ?
….-1/9 +pi x 4 = 1 – 1/3+1/5 -1/7
לא ראיתי ממך התייחסות ?
(אם לא ברור מה רשום למעלה –
זה דרך לבטא את פיי כסכום של סדרה אינסופית.. )
זה לא מרמז איכשהו שיש לפיי ערך קבוע ?
2.0003 מ"מ עאלק………………
על 0.00000000020003 מ"מ בדקת, חכמולוג?
מדדת את הקוטר של פרוטון, לפחות, בר-מוח?
סיבובים גיאומטריים בדאלק….
אולי נפל לך גרגיר של אוכל חתולים לתוך המכונה המדהימה שלך בזמן אחד הסיבובים?
מדען דמיקולו…
מה אתה, סתם משעמם לך אדון עצבר א..רכמידס?
עצבר הגאון
אתה מתעקש לא להבין.
המכשיר שלך עקום ויש לך סטיה במדידות.
קאפיש, מיי פרנד?
האקדמיה פשוט בוגרת מספיק כדי לא להתייחס לקישקושים המקושקשים שלך, זעטוט חסר כל פשר שכמוך.
ותפסיק לכתוב תחת שמות מפוברקים ותארים שאינם משוייכים אליך.
אידיוט.
אכן דרמטי, עצבר.
דרמטי גם זה שאתה מרצה לי על להתאמץ – ממציא פורץ דרך שמתעצל לבצע ניסוי של 20 דקות..
לישראל
הפעם היית צריך לצרף חישוב, הרי ציינתי את נתוני ציר הפלדה.
אם תתאמץ ותערוך את החישוב, תראה שתוצאת המדידה חרגה מתחום השגיאה , ולכן אין ספק שפאי של קוטר 2 מ"מ (קצת יותר גדול) מפאי של קוטר 120 מ"מ
וכל השאר….היסטוריה
אבל כפי שחזרתי ואמרתי, ניסוי ההיקפן בא ליצור דרמה מדעית
פעם ראשונה בהיסטוריה של המדעים המדויקים,
ניסוי מכני מגלה אמת מתמטית, שהמתמטיקה בכלל לא מסוגלת לגלות.
אתה מבין….למתמטיקה אין בכלל יכולת לגלות את רעיון פאי המשתנה.
דרמה….אתה מבין ?
המעגלים לא שייכים למתמטיקה ולחישובים שלה, אלא הם שייכים לפיזיקה ולמדידות שלה.
דרמה…אתה מבין ?
מה שמכונה "הקבוע המתמטי פאי" פשוט נעלם מעולם המדע
דרמה ,אתה מבין ?
2000 שנים נמסרה טעות מתמטית של פאי קבוע מדור לדור, ואף מתמטיקאי לא הרגיש בה
דרמה ,אתה מבין ?
עם הרעיון השגוי של פאי קבוע, המתמטיקה עיכבה את הופעתה של הגיאומטריה העצברית, שהיא גיאומטריה פיזיקלית המבוססת על מדידה מדויקת שהמדע בכלל לא הכיר.
דרמה ,אתה מבין ?
המדע גם לא הכיר את ההיקפן
בסך הכל אין לי טענות,כיוון שאני עובר מסלול מכשולים רגיל , של שינוי פרדיגמה.
ההתענינות שלך בניסוי ההיקפן, הייתה מועילה.
תודה
אתה צודק עצבר, כמו תמיד.
אין כל צורך לחזור על ניסוי ההיקפן עם פי 10 או 100 סיבובים – כבר הוכחת לשביעות רצון כולם, כולל האקדמיה, שפאי של כל המעגלים זהה, בתחום שגיאת המדידה.
תודה עצבר על הניסוי המעולה שהסיר כל ספק. נראה לי שהאקדמיה תסתפק בניסוי שלך ואין צורך לחזור על הניסוי – בדיוק כפי שאמרת!
המשך בדרך זו.
אני רובי ריבלין.
חחח עצבר התדרדרת להמציא דמויות בראש שלך שתומכות בך?
אני מוכן להתערב ש"תומר" לעולם לא יזדהה בשמו האמיתי, או יפנה לעבודת המסטר שלו.
אם הוא היה דוקטורנט אמיתי לא היה חושש להזדהות. אבל שמו האמיתי עצבר… עצוב ביותר
התגובה האומרת שגם 10000 סיבובים לא יעזרו, אם קוטר הגליל הוא 2.001 מ"מ ולא 2 מ"מ, היא ממש לעניין.
לידיעתך את הגליל הזמנתי בארה"ב, והוא הגיע אלי עם מסמך של מעבדת מדידה מוסמכת.
אורכו 50 מ"מ, קוטרו באמצע 2.0003 מ"מ , בצד 2.0004 מ"מ , ובצד האחר 2.00025 מ"מ
החלק השני של תגובתך האומר שיש לפאי ערך מוגדר…הוא מלל חסר פשר, שאינו מובן לכותב ואינו מובן לקורא.
לתומר, מצורף המאמר כמתנות במקום מתמטיקה, ותודה על העידוד.
וישראל, אין לך ברירה אלא להתאזר בסבלנות, ולהמתין שנציג האקדמיה של המדעים המדויקים יחזור על ניסוי ההיקפן . זה באמת ניסוי דרמתי, אך אין בו צורך , מכיוון שההוכחה הגיאומטרית שצירפתי (שהיא אינה דרמתית) קובעת שפאי משתנה ואינו קבוע.
או שתומר הוא טרול שמטריל את הטרול
או שתומר נהנה מהויכוחים פה ורוצה שימשכו
או שאצבר התחיל לכתוב בעוד שם.
עאלק דוקטורנט.
אדון תומר למה שלא תזדהה בשם מלא ותכתוב איפה אתה עושה דוקטורט?
הרי אין שום סיבה להתבייש בזה.
ואיזה רעיונות זה מחבר לך? (בטח כולם של עצבר על שטויות של זמן פאסיבי)
עצבר צודק ואתם לא הבנתם.
הוא מטריל כי אנחנו פה החברים היחידים שלו בעולם, היחידים שבכלל מתייחסים איליו.
ותודה לעצבר שביצע את ניסוי ההיקפן, שמראה שלכל המעגלים אותו הפאי בתחום שגיאת הניסוי.
ולכן אין צורך לחזור על הניסוי, עצבר צודק עוד הפעם.
לאעצבר שלום.
רציתי להודות לך על שיתוף הרעיונות המרתקים שלך.
אני דוקטורנט בתחום מתמטיקה שימושית באוניברסיטה. ובהחלט נתת לי הרבה חומר למחשבה, ועזרת לי לחבר בין כמה רעיונות שכבר הרבה זמן מעסיקים אותי. זה מאוד מתחבר ורלוונטי למאמר מדעי שאני כותב כרגע לצורך קבלת התואר.
תודה שוב,
ואל תתן לכל קטני האמונה לייאש אותך
אצבר אינו מבין רעיונות ברמת תיכון – שגיאת מדידה, ומתעלם מהניסוי של עצמו שמוכיח שPI קבוע עד כדי שגיאת המדידה (כאילו דה!)
הטרחנים הכפייתיים המתמטיים, לפי דודליי, הם כמעט תמיד גברים, וכמעט תמיד מבוגרים, לרוב בשנים שלאחר הפרישה מעבודה. הם אינם מבינים מה משמעות הטענה המתמטית שדבר מסוים אינו אפשרי. הידע שלהם בתחום שבו הם פועלים חלקי ביותר, ובדרך כלל הם חסרי השכלה פורמלית. הם סבורים שהבעיות שהם תוקפים הן בעלות חשיבות רבה, ונוטים לחשוד שזכויות היוצרים ייגנבו מהם. מעל לכל, לא ניתן לשכנע אותם שהם טועים.
בשל חוסר ההכרה בתגליות שלהם, טרחנים כפייתיים טוענים במקרים רבים לקונספירציה לה שותף הממסד המדעי המתנכל להם ומתכחש בכוונה לאמת. טרחנים משתמשים במונחים שהומצאו על ידם שאין להם הגדרה ברורה ונמנעים משימוש במונחים ברורים ומוגדרים היטב. כשהם מתבקשים להסביר את מינוחיהם, הם נוטים לעשות זאת באמצעות מונחים מעורפלים באותה המידה.
פעמים רבות הבעיה הבסיסית בטענותיהם של טרחנים כפייתיים היא חוסר הבדלה בין הגדרות, עובדות ודעות. תוצאות הסותרות את האינטואיציה שלהם נפסלות על ידם, לכאורה על ידי נימוק ריגורוזי אולם למעשה פעמים רבות טיעונם מורכב מרבדים רבים של טענות והגדרות שבבסיסן אין עקביות או שהנימוק היסודי מתבסס על הנחה אינטואיטיבית
גם 10000 סיבובים לא יעזרו, אם הגליל הפנימי הוא 2.001 ולא 2.0 ממ
היחס השגוי לעומת רדיוס הגליל החיצוני ישאר שגוי לא משנה כמה סיבובים מדובר..
הדיוק המרבי של חריטה הוא בערך 2מיקרומטר , כך שהניסוי מלחתחילה שגוי.
המאמר המהולל שאתה מנסה לשווק כאן באינטנסיביות, יותר מזכיר כתבה בירחון הילדים אצבעוני. גם בתוכן גם בניסוח וגם במעטפת.
שלא לדבר על זה שאתה בוחר משום מה להתעלם מהעובדה הפשוטה שיש לפיי ערך מוגדר חד חד ערכית כטור מתכנס
חבר אתה חופר..
היות ויש וויכוחים חסרי טעם בעניין ניסוי ההיקפן, אני מציע לוותר על הניסוי – שבא להציג באופן דרמתי את רעיון פאי המשתנה – ולהסתפק בהוכחה גיאומטרית פשוטה של רעיון זה.
http://img2.timg.co.il/forums/2/5604aa4e-34d1-49c7-86a2-4905ab2f0392.pdf
לחזור עליו עליו כמובן עם דיוק רב יותר. עם יותר סיבובים.
הקשקוש היחיד פה הוא של עצבר עצמו. הסירוב שלו להפעיל את ה"ניסוי" של עצמו ליותר סיבובים (20 דקות עבודה).
אז הוא מקשקש על זה שהוא מחכה למכון ויצמן.
"ניסוי" ה"הקפן" מוכיח שPI קבוע עד כדי שגיאת הניסוי.
עצבר הבין שה"ניסוי" שלו מוכיח שהוא טועה, וש"כלי המדידה" שהוא עצמו בנה מוכיח את זה. עם יחזור עליו עם יותר סיבובים הניסוי שלו יוכיח את זה בדיוק הולך וגובר.
אבל אדון עצבר נתלה על מישהו אחר (טכניון/ויצמן) שיבזבז את הזמן שלו על משהו שהוא עצמו הוכיח שזה שטויות. העובדה שכולם הבינו שהוא טרול היא הוכחה בעיניו ש"מפחדים מהשינוי"
ברור שעצבר לא יפעיל את ה"ניסוי" שכבר מוכן אצלו בחצר, כי אז הוא יאלץ להודות שכמו כל טרחן כפייתי הוא בזבז עשורים שלמים מהחיים שלו על שטויות. זה הפחד הכי גדול שלו.
הצטרפו לקריאה אל האקדמיה של המדעים המדויקים
http://img2.timg.co.il/forums/3/51ea21af-238b-4926-8045-06105f2e4ed6.pdf
התגובה היחידה ל"ניסוי" ה"היקפן" היא לחזור עליו
אם מי שטוען את הטענות המגוחכות בנה "ניסוי" ומסרב לחזור עליו ומצפה שמישהו יתיחס אליו ברצינות…
הוכחת שאתה בדיחה שלא מאמינה בעצמה בשטויות שלה
1. עצבר טוען שבעזרת קובייה הוא יכול לנחש מחשבות.
2. עצבר צודק כשהוא מנחש שהנסיין חשב על המספר "6".
3. עצבר יכול להפריך/לאושש את הטענה המהפכנית ע"י הטלת קוביה 100 פעם
4. עצבר לא עושה את זה ומחכה למכון ויצמן
מ1-4 נובע שעצבר מפחד או שרלטן
קל ופשוט להגיב לניסוי ההיקפן, עם קשקוש מילולי
המתמטיקה לא טועה, והיא הוכיחה כי פאי קבוע
המכניקה תמיד לא מדויקת, ולכן הניסוי פגום
מה פתאום שתופיע מדידה בתחום הגיאומטרי, מעולם לא היה דבר שכזה.
מכניקה בתחום הגיאומטרי ? הרי זה המקום של הלוגיקה הטהורה, ושל רעיונות אידיאליים.
שניסוי מכני יפסול הוכחה מתמטית ? הרי המתמטיקה היא מלכת המדעים.
הרעיון של פאי קבוע קיים אלפי שנים מאז ימי ארכימדס, וכל המתמטיקאים קיבלו אותו,
אפשר גם להתעלם מהניסוי כאילו לא היה, וכלל לא להתייחס אליו.
את התוצאה של ניסוי ההיקפן אפשר להפריך רק עם ניסוי חוזר, ולא עם דיבורים.
הניסוי הוא הפוסק האחרון במדע, ויש לקבל את פסיקתו.
הניסוי הזה אמור לאתגר כל מוסד מדעי בארץ ובעולם, ומעניין מי מהם יבחר להגיב.
זהו ניסוי פיזיקלי של מדידה מכנית מדויקת שהמדע כלל לא מכיר, שבהכרח ייצור זעזוע במתמטיקה ובגיאומטריה.
הזעזוע הצפוי במדעים המדויקים הוא כנראה הבלם , שמעכב את הופעתו של ניסוי חוזר.
אבל כולנו יודעים שאי אפשר לעצור את התפתחות המדע, כך היה וכך יהיה.
עצבר
שים לב (אם יש לך אחד כזה), היחס נשאר אותו יחס.
האדם הוא אדם. רק האיי קיו שונה.
בדיוק כמו בעניין שלך:
הפאי נשאר באותו יחס רק הגודל של המעגל שונה…
אולי ההבדל במדידות שלך נובע מתוך טעות מדידה ברמות ננומטריות, כתוצאה ממכשירים עקומים מספיק?
עצבר
אדם עם איי קיו של 2 שונה מאדם שיש לו איי קיו של 120.
מה הטענה שלך?
רק העובדה שהלכת ובנית את המתקן ועכשיו שיש לך אותו אתה מתעקש לערוך את הניסוי בדרך מוטה שמראה כביכול על הצלחה אך אתה וכולם יודעים שאין לניסוי כל ערך בפחות ממספר רב של סיבובים, מעידה על ערכך כמדען ונסיין.
לפחות כולם רואים בזמן אמת את פרצופם האמיתי של כל הטרחנים הכפייתיים – משועממים, גלמודים, בונים תילי תילים של ״תאוריות״ ו״הוכחות״ שכל תכליתן לפאר את האגו של ה״ממציא״ ושאינם מוכנים לקבל כל הפרכה לטענותיהם השגיוניות.
עצבר מוכיח 1:
הוא טרחן כפייתי שהודה שדרמה מומצאת עדיפה עליו מניסוי פשוט (שכבר בנה את כל מערך הניסוי בשבילו) שתוכיח שהוא טועה.
עצבר מוכיח 2:
הוא לא מבין מושגים בסיסיים שכל תלמיד תיכון מכיר
ניסוי ה"היקפן" (עאלק המצאה) הוכיח:
PI קבוע עד כדי שגיאת הניסוי
אריסטו לא ביצע את הניסוי כי השיטה המדעית (היפותיזה – ניסוי) עוד לא הייתה מקובלת.
הוא חשב שאם הגיע למסקנה הגיונית (מבחינתו) אין צורך בניסוי
איזה קשקשן.. אין לך ספק..
כבר אמרת שאינך מבצע את הניסוי האמיתי בגלל הדרמה. אילו היית מדען אמיתי ולא שרלטן חרטטן, היית מבצע את הניסוי ושוכח מהדרמה.
אין לי ספק בתוצאה של ניסוי ההיקפן
פאי של קוטר 2 מ"מ ( קצת יותר גדול ) מפאי של קוטר 120 מ"מ
יש לך ספק ? חזור על הניסוי בעצמך
אינך יכןל לחזור על הניסוי ?
תמתין בסבלנות לפיזיקאי הנועז שיחזור על הניסוי.
גם אני ממתין לתוצאה הדרמתית הצפויה.
עוד חרטה ברטה, אחיזת עיניים.
אריסטו לא ביצע את ניסוי הנפילה חופשית כי לא חשב שזה הכרחי או שלא ידע איך לעשות זאת. זה לא שהוא ביצע אותו והיה ספק רב במידת הדיוק של הניסוי.
אתה ביצעת את ניסוי ההיקפן ויכול לחזור על הניסוי היום כדי לקבל את מידת הדיוק הנכונה. עצם זה שאתה מסרב לערוך את הניסוי המדוייק מעיד על מידת האינטגריטי שלך כאדם ו״מדען״.
מדען עלק.. אתה בטח רואה את עצמך באותה שורה עם אריסטו וגלילאו אה? או שאולי גם הם קטנים על עצבריהו?
אבל באותו עניין שאלה מעניינת לפורום:
אם נפיל ממגדל גבוה בארץ בהפרשי זמן 2 גופים במשקל שונה, מי יגיע לארץ במהירות גבוהה יותר, הקל, הכבד, או ששניהם יגיעו באותה מהירות?
אריסטו טען – כי בנפילה חופשית – הגוף הכבד יותר מהיר יותר, ולכן אם נשחרר באותו רגע אבן וגזיר עץ מראש מגדל , האבן תגיע ראשונה אל האדמה. זהו ניסוי בתחום התופעות הזעירות, והוא אמור לגלות הפרש זעיר כמו 0.01 מ"מ, ניסוי כזה לא נערך מעולם, מכיוון שקשה מאוד לבצע אותו.
אם אריסטו היה עורך את הניסוי ומוכיח את טענתו, ספק אם גלילי היה עורך את הניסוי המפורסם שלו, בנפילה חופשית.
גילוי נאות: יש קשר בין הניסוי האריסטוטלי שלא נערך, לניסוי ההיקפן .
״יש הרבה מדענים שלא לקחו אותם ברצינות, ובפרט אם הם מציעים שינוי פרדיגמה״.
חרטה ברטה, כמו תמיד.
הראה לי ולו מדען אחד בהסטוריה שהיה לו ניסוי ״סלאם דאנק״ שהיה יכול לבצעו ולהוכיח את צדקתו, והוא לא ביצע אותו.
בידיך ניסוי כזה כולל כל הציוד הנדרש – ניסוי ההיקפן עם פי 100 סיבובים – ואתה לא מבצע אותו בגלל שיקולי ״דרמה״.
מילא שאתה מנסה ללא הצלחה לאחז את עיני כולם – אך מה עם עיניך שלך, עצבר? אתה הרי יודע את האמת, שאו שבצעת כבר את הניסוי (20 דקות) או שאינך מבצע אותו כי אתה יודע היטב שאחר כך לא ישאר דבר מכל הגיאומטריה והפיזיקה העצברית המפוארת, ותיאלץ להתמודד עם אפרוריות היום יום המייאשת שבה אתה סתם הוזה בהקיץ, חרטטן בבלוג..
יש הרבה מדענים שלא לקחו אותם ברצינות, ובפרט אם הם מציעים שינוי פרדיגמה
https://alaxon.co.il/article/%D7%94%D7%9E%D7%94%D7%A4%D7%9B%D7%9F-%D7%94%D7%9E%D7%AA%D7%9E%D7%99%D7%93/
ניסוי ההיקפן אמור לשנות פרדיגמה בגיאומטריה, במתמטיקה, וגם בפיזיקה.
ניסוי ההיקפן גם כולל המצאת מכשיר מדידה , שמבצע מדידה חדשנית בתחום הגיאומטרי.
אז אל תתפלא שלא לוקחים אותי ברצינות, זה ממש מתבקש , ואני כלל לא מתרגש.
יאללה חלס עצבר, אמרת כבר ברגע של אמת שהמניע שלך הוא בדידות ושיעמום. אף אחד לא ייקח אותך ברצינות בגלל שאתה שרלטן מדעת, אחרת היית עושה כבר את ניסוי ההיקפן האמיתי, לא החרטה ברטה שעשית.
ההצעה שלך לא טובה, כיוון שהיא מבוססת על הגיאומטריה של דקארט
הגיאומטריה של דקארט עיכבה את הופעת הגיאומטריה הפיזיקלית.
בגיאומטריה של דקארט יש כלי עזר , והוא מישור ממשי שעליו מצוירת נקודה , המסומנת באפס.
נקודה זו משותפת להתחלה של שני קווי סרגל המצוירים במישור הזה , קו סרגל אופקי, וקו סרגל אנכי.
על גבי כלי עזר זה אפשר לסמן נקודות שמקומן נקבע על פי מספר סרגל אופקי , ומספר סרגל אנכי.
את המספרים של הנקודות מפיקה נוסחה כמו לדוגמה y=xx
אם נביט מרחוק באוסף נקודות צפופות של נוסחה זו, בקלות אפשר יהיה לטעות ולחשוב שמדובר בקו עקום, ולא באוסף של נקודות.
היות ומדובר באוסף של נקודות ולא בקו עקום, השם המתאים לאוסף נקודות כזה , הוא נקדן עקום.
בגיאומטריה של דקארט אין קווים, ובמקומם יש נקדנים.
כשהופיעה הגיאומטריה של דקארט, כבר לא היה צורך לצייר קו בעזרת עיפרון, והיה מספיק להשתמש בנוסחה המפיקה נקודות. בגיאומטריה של דקארט אין קו עגול סגור הנוצר בעזרת מחוגה, ובמקומו יש נקדן עגול הנוצר מהנוסחה xx+yy=1
יש הבדל תהומי בין קו עגול סגור לנקדן עגול.
לקו עגול סגור יש אורך ממשי כמו לדוגמה 45 ס"מ, וצורה אחידה ייחודית הנתפסת במבט פשוט.
ואילו לנקדן עגול אין אורך ממשי, ואין צורה.
אסור לצייר את נקודותיו של נקדן עגול, כי לנקודה מוחשית יש אורך ממשי, רוחב ממשי, וגם צורה.
לנקדן עגול יש קיום רק במערכת הצירים של דקארט, עם נוסחה מתאימה.
בגיאומטריה של דקארט מושג הקו לא קיים, ובמקומו נמצא הנקדן.
הנקדן הוביל את הגיאומטריה אל קיפאון שעיכב את הופעת הגיאומטריה הפיזיקלית.
שים לב , זה קשור להצעה שלך
ניוטון ולייבניץ לא הרגישו בקיפאון זה, והם הציעו חשבון שאמור לטפל בקווים עקומים ועגולים.
חשבון זה כלל לא מטפל בקווים עקומים ועגולים, אלא בנקדנים עגולים ועקומים הנתפסים כקווים ישרשרים. (קו ישרשר בנוי מקטעי קו ישר)
לכל קו עגול סגור יש אורך ממשי וצורה אחידה ייחודית.
לכל קו עקום יש אורך ממשי, וצורה ייחודית
הנתונים האלה לא מופיעים בחשבון הניוטוני, ובמקומם מופיע קו ישרשר עגול, או קו ישרשר עקום.
התוצאה מהחלפת קו עגול בקו ישרשר עגול
הוא חשבון לא מדויק
החשבון הניוטוני יהיה בהכרח לא מדויק, ולכן הוא לא היה מסוגל לגלות את הקשר בין האורך הממשי של קו עגול סגור, למספר היחס בינו ובין אורך הקוטר הישר.
את הקשר הזה גילתה הגיאומטריה הפיזיקלית
המתמטיקה צריכה לערוך ביקורת על כל פעילותה בתחום הגיאומטרי הרציף, על רעיון השאיפה לאפס ולאינסוף, על תוקפו של החשבון הניוטוני, על הכישלון בטיפול קווים שאינם ישרים, על המושג היסודי של הגיאומטריה, והגיע הזמן להבדיל בין גיאומטריה מתמטית המסוגלת לטפל בקטעי קו ישר, לבין גיאומטריה פיזיקלית המסוגלת לטפל בקווים עגולים ועקומים.
א.עצבר 1/4/2021
קורס מבוא בחשבון אינטיפסמלי שנה א באוניברסיטה?
*מבוא* ליחידה *תיכונית* אחת יספיק (פרק המבוא למעבדה)
מכסים שם נושאים איך עורכים ניסוי, מה זה מעבדה, *שגיאת ניסוי* וכדומה
הייתי מציע קורס מבוא בחשבון אינטיפסמלי שנה א באוניברסיטה.
יסבירו לך על נגזרות ואינטגרלים, ולמה –
…1/9 +pi x 4 =1-1/3+1/5 -1/7
ועוד כמה דברים שאולי קשורים ,אבל אני מניח שלא מכבודך.
אגב, אם מקודם חשבתי רק שאתה לא מבין כלום במתמטיקה, פיסיקה תאורטית ,פיסיקה נסיונית, וכמובן בכתיבה מדעית, עכשיו גם ברור שבכתיבת שירים אתה ממש גרוע.
שילוב של טרחן כפייתי עם תסביך נפוליאון, שחרר אותנו.
הצטרפת למשוררים אנונימי…בהצלחה
קח מחוגה, שרטט על דף A4 מעגל בקוטר 2 ס"מ, ומעגל בקוטר 8 ס"מ
זהה את הקו עגול סגור השייך לקוטר 2 ס"מ, ובוודאי תבחין כי יש צורה אחידה
זהה עתה את הקו העגול סגור השייך לקוטר 8 ס"מ, ובוודאי תבחין כי יש צורה אחידה, אבל היא שונה מהצורה האחידה הקודמת.
מכאן כבר מתפתחת גיאומריה חדשה של קווים עגולים סגורים, שיש בהם קשר ברור בין אורכם הממשי (אורך ממשי זה ציוצג בשיטה פיזיקלית של כמות סנטימטרים) לבין צורה אחידה ייחודית.
לכל קו עגול סגור יש אורך ממשי מסוים ,וצורה אחידה ייחודית.
לכן, קווים עגולים סגורים אינם דומים זה לזה
לכן, מעגלים אינם דומים זה לזה
פירוט נוסף במאמר הבא
http://img2.timg.co.il/forums/3/45317ede-eca8-48bc-8608-477e5a47c910.pdf
מר. א. עצבר, אסקווייר
המשורר הדגול וממציא ההיקפן האגדי,
הוד רוממותו רואה נסתרות ושומע קולות,
הני עבדך מבקש בזאת, במטותא ממך, תוכל להשיב על שאלתי מקודם (ציינתי בפניך שלא הבנתי במה "הבחנת" אז רציתי לדעת במה "הבחנת")?
תודה תודה תודה
(משתחווה)
– מחיאות כפיים…
סוף
אז מה גורם לשדה מגנטי של מיואון להציג ערכים שונים מן המצופה?
מהי האפשרות הסבירה יותר על פי המומחים הבכירים?
(חומר ואנרגיה אפלים? סבדרמיש משחק עם הלייזר? השערות, מישהו?)
נו שויין עצבר, בהצלחה בדרכך החדשה כמשורר במאי ופובליציסט.
רק אל תצפה ממישהו לקחת ברצינות את הגיאומטריה והפיזיקה שלך..
מדוע אתה שואל ? כנראה שאין לי תשובה טובה
אולי כי זה טבעו של האדם,
הצייר רוצה שייראו את הציורים שלו,
הכנר רוצה שישמעו את נגינתו,
ישראל שפירא רוצה שישמעו את דבריו,
שחקנית התיאטרון רוצה שייראו את הופעתה
הנגר רוצה שייראו את הרהיטים שהוא מייצר
הרופא רוצה לראות את החיוך של האדם שחזר לבריאות תקינה
המשורר רוצה שיכירו את השירים שלו
והסופר את הסיפורים שלו
ואני רוצה שיכירו את רעיון פאי המשתנה
אופה הלחם רוצה שיטעמו ויכירו את הלחם שלו.
והזמר רוצה שישמעו את קולו
וכן הלאה
וכן הלאה
זהו האדם, וזו דרכו להתחבר עם בני אדם, כמו שנאמר לא טוב היות האדם לבדו
אנחנו קטנים עליך עצבר, איננו ראויים לגדולתך. אנו אנשים פשוטים שמתעניינים רק במדע, לא בדרמה. בגלל זה אנו מגיבים ב״הידען״, בלוג מדעי, ולא בבלוגים של דרמה.
השאלה היא מדוע מדען על כמוך זקוק בכלל להכרתינו, או של הממסד המדעי, הרי גם הם קטנים עליך, אנשים בינוניים שכמותם..
לישראל שפירא
לא דייקת ישראל שפירא, אני מעוניין בדרמה מדעית, ולא בדרמה רגילה של נפתולי הנפש האנושית.
כל הנתונים של דרמה מדעית נמצאים בסיפור ההקפן, וצריך רק לשבץ אותם נכון.
אפילו אתה שמכיר היטב את הנושא, אינך יודע אם הניסוי הצליח או נכשל, אף על פי שאין צורך בניסוי מעשי כדי לדעת זאת.
כל שנדרש הוא קצת דמיון וקצת היגיון, כדי להגיע אל הפתרון.
אז מה הטעם לוותר על דרמה מדעית, ולסובב 600 סיבובים במקום 60 ?
הדרמה המדעית הרבה יותר גדולה בקשר לזמן הפסיבי.
החומר , המושג הפיזיקלי הראשון נוצר מצירוף כמויות של זמן פסיבי ואנרגיה,
והוא בגדר של צורה פיזיקלית.
הרעיון של צורה פיזיקלית, דוחה את הרעיון הניוטוני שהחומר הוא מושג כמותי, וכוח המשיכה משקף את הכמות הזו.
זמן פסיבי הוא הוא מושג דרמתי פיזיקלי חדש לחלוטין, ותפיסת החומר כצורה פיזיקלית, כבר חייבה את כתיבת השיר הבא.
קוסמולוגיה פיוטית 7/6/16
הזמן הפסיבי עוטף אותנו,
ואנו נעים דרכו.
שאלתי אותו, ולא נעניתי.
חכה קצת זמן
הוא אמר
מי אתה ? שאלתי ומיד נעניתי
אני הזמן הפסיבי,
אני שייך לטבע
אני מוביל את האור והצבע.
איפה אתה ? הקשיתי
אני ממלא את המרחב הנורא,
והוא עתה מלא נהרה
האנרגיה גם איתי, עוצמתה ללא אומר,
וביחד, אנו יוצרים את החומר.
אני מכיר את החומר, אמרתי
נגעתי בו והוא ממש כאן
בי לא תוכל לנגוע
אבל בתוכי אתה חופשי לנוע.
האם אתה באמת זמן ?
הרי הזמן שאני מכיר, תמיד בורח.
לי אין עבר – אמר הזמן הפסיבי – גם לא עתיד.
אני תמיד כאן, אני לא אורח.
אני הוא הזמן האמיתי
והאנרגיה תמיד איתי.
Aetzbar
אבי בליזובסקי.
עצבר מטריל ומציף את התגובות ולא בא לקרוא באתר. אני רוצה לקרוא תגובות של אחרים והן טובעות בתגובות שלו. *רוב* התגובות הן שלו, וזה לא הכתבה היחידה שזה ככה.
חחח עצבר המסכן. פונה לעאלק פסיכולוגיה הפוכה. זה מתאים למי שאכפת לו מעצבר או מהרעיון המופרך שלו. למי אכפת מדרמה שקיימת רק אצלו בראש?
נגמר לו הפסאודו-מדע אז הוא עבר לרגש.
עצבר לא מבין מושגים בסיסיים ברמת בגרות (כמו שגיאת מדידה).
כי אז הוא יבין שבעצם המתקן המטופש שלו מוכיח שPI *קבוע* כדי שגיאת הניסוי…
האמת עצבר, נראה לי שענית ויפה ענית.
אתה מעוניין בדרמה, לא במדע.
אתה מבין שהניסוי במתכונת שביצעת אותו הוא חרטה ברטה, אתה יודע איך לבצע אותו בצורה הנכונה, יש לך את הציוד והזמן, אך אתה לא תבצע אותו כי אתה מעוניין בדרמה.
אנשי מדע אמיתיים ביצעו את ניסוייהם בעצמם לפני שדרשו הכרה – גליליאו עם המשקולות, פרנקלין עם העפיפון, לבואזייה עם המבחנות ועוד רבים.
ורק עצבר שטוען שהמציא גאומטריה ופיזיקה חדשות תובע שהממסד יבצע את הניסוי פורץ הדרך שלו בלי שהוא יבצע אותו בעצמו..
אפילו אם אתה צודק, מיתגת את עצמך בקטגוריה שונה לגמרי מכל המדענים בעולם. זה כאילו שפלוני טוען שבנה פרפטום מובילה, מפרסם את עיקרי הפיזיקה החדשה שדרושה לפעולתה, ודורש שינסו את המכונה שלו בלי שניסה אותה בעצמו..
אז למה שמישהו ייקח אותך ברצינות, עצבר?
אבל למה שמוסד מדעי יערוך את הניסוי האמיתי (100 סיבובים לגלגל הגדול, לא 1, 1 זה חרטה) אם ההוגה עצמו לא מבצע אותו?
מדוע אתה שואל ? מכיוון שאני לא מעוניין לסלק את הדרמה מניסוי ההיקפן.
בשלב זה התעלומה קיימת, וכל אדם יכול לטעון כי המכשיר לא מדויק , הקטרים של ציר הפלדה וגלגל הפלדה לא מדויקים, ולכן יש ספק גדול אם הניסוי מבשר על מהפך גיאומטרי מתמטי.
בשלב זה יש גם ספק אם המושג העצברי "גיאומטריה פיזיקלית" הוא אמיתי או שמדובר במלל חסר פשר.
אלה הם נתונים לדרמה מדעית, וכל הדרמה תיעלם אם ציר הפלדה שקוטרו 2 מ"מ
יסתובב 600 סיבובים ולא 60.
אני מעוניין שמוסד מדעי מכובד יחזור על הניסוי עם 60 סיבובים, ויופתע מהתוצאה .
תוצאה זו תטיל ספק בפעילותה של המתמטיקה בתחום הגיאומטרי הרציף , ותחייב לשנות מוסכמות מתמטיות הקיימות מאות בשנים.
המוסכמה החשובה ביותר במתמטיקה היא זו שאין טעויות במתמטיקה.
אתה מציע לבטל את הדרמה הזו ?
אתה מציע לבטל את הדרמה ? שבה "פלוני אלמוני המכנה עצמו עצבר" יצר מהפך גיאומטרי מתמטי בעזרת הקישור למדידה פיזיקלית לא מוכרת למדע, במכשיר מדידה מדויק שאינו מוכר למדע.
אם אתה רוצה לראות את הדרמה הזו, הקם קבוצת תמיכה שתנסה לשכנע את מכון ויצמן או את הטכניון לחזור על ניסוי ההיקפן.
ויפה שעה אחת קודם.
אוי עצבר, יחס ישיר יכול להיות גם שלילי.. כיתה ו3.
אבל מדוע באמת שלא תבצע את הניסוי עם מספר סיבובים גדול יותר? כאחד שזועק את צדקתו שנים רבות כל כך, טוען להתעלמות הממסד המדעי ומבקש הכרה – מדוע שלא תשקיע 20 דקות מזמנך כדי להוכיח את נכונות טענותיך? אם זמנך כה יקר, מדוע שלא תבקש ממתנדב לערוך את הניסוי?
הייתכן שממציא ההיקפן יודע היטב שהניסוי שלו אינו מוכיח דבר?
היעלה על הדעת שההוגה המיתולוגי של המתמטיקה העצברית והזמן הפסיבי הוא פשוט שרלטן מאחז עיניים ולא גאון על שהממסד המדעי המאובן מתעלם ממנו כי הוא חושש מן הבשורה שבפיו?
זה מה שכתבה בהתחלת תגובתך
אליהו
האם עצבר הוא טרחן כפייתי כדבריך שאינו מודע לכך, שרלטן במודע, או שאולי הוא בכלל צודק ופאי אכן קטן ביחס ישיר לקוטר המעגל?
ולגבי החזרה על הניסוי , אני משאיר זאת למוסד מדעי מכובד, שהקהילה המדעית בארץ ובעולם תקבל את התוצאה שהוא ישיג.
אם הוא יפסוק שפאי של קוטר 2 מ"מ = לפאי של קוטר 120 מ"מ , אז בהחלט אודה שטעיתי, ובזבזתי לריק שנים רבות על מחקר שהוא כישלון מוחלט.
אבל אם הוא יפסוק שפאי של קוטר 2 מ"מ, הוא "טיפה יותר גדול" מפאי של קוטר 120 מ"מ , תבוא גאולה למדעים המדויקים, מתמטיקה, גיאומטריה, פיזיקה.
זה מה שכתבתי, לא?
״מה שלטענתך מוכיח שפאי של הגליל הקטן גדול מפאי של הגלגל הגדול״.
האם תערוך את ניסוי ההיקפן עם פי 100 סיבובים או פי 10 ותוכיח לכולנו שאנחנו טועים?
מה המשותף בין המאמר הזה הדן במודל הסטנדרטי של החומר, לניסוי ההיקפן ?
התשובה היא – ניסויים בתחום התופעות הזעירות שקשה מאוד להבחין בהם.
ומה המבדיל ? הניסוי של המודל הסטנדרטי , אינו קשור למציאות הפיזיקלית, כיוון שהחומר הוא בגדר של צורה פיזיקלית. ( החומר אינו מושג כמותי והוא בנוי מצירוף כמויות של אנרגיה וזמן פסיבי)
לעומת זאת, ניסוי ההיקפן עוסק במציאות פיזיקלית ממשית, של גלילי פלדה בעלי צורה גיאומטרית מדויקת מאוד, שבהם מופיעים קווים עגולים סגורים חסרי עובי. (הדגש – חסרי עובי)
את קוטרם של גלילים אלו אפשר למדוד עם סטייה של מחצית אלפית מ"מ, וההיקפן מצליח להשיג
את מספר היחס בין ההיקפים שלהם.
מדידת יחס מדויק בין היקפי גלילים היא הראשונה בהיסטוריה המדעית, והיא שהביאה לעולם את המושג "גיאומטריה פיזיקלית" שהיא הגיאומטריה של קווים עגולים סגורים.
הגיאומטריה של הקו הישר היא גיאומטריה מתמטית, המבוססת על משפט פיתגורס.
ההיפך ישראל, ההיפך…
פאי הולך וגדל, כאשר קוטר המעגל הולך וקטן…
בקשר הזה אפשר להבחין, גם בלי ניסוי מעשי.
http://img2.timg.co.il/forums/2/5604aa4e-34d1-49c7-86a2-4905ab2f0392.pdf
הניסוי המעשי רק הוכיח את "כיוון השינוי" , כאשר הוא קבע שפאי של קוטר 2 מ"מ , "טיפה יותר גדול"
מפאי של קוטר 120 מ"מ.
כאשר נקבע הכיוון של שינוי פאי, היה צריך לשער את ערכו של פאי מקסימלי.
ההשערה שלי הייתה 3.164 , והשערה זו צריכה לעמוד במבחן
את ערכו של פאי מינימלי לא היה צורך לשער, כיוון שכל החישובים המתמטיים לגבי פאי, היו עם קטעי קו ישר (משפט פיתגורס תקף רק לקטעי קו ישר)
קטע זעיר מקו ההיקף של מעגל (שקוטרו מתקרב לאינסוף מ"מ) הוא קו ישר, ולכן התוצאה המתמטית המפורסמת של 3.1415927 מתאימה למעגל שקוטרו מתקרב לאינסוף מ"מ
וכאן סיימה המתמטיקה את תפקידה, מכיוון שהיא מסוגלת לחשב רק את פאי מינימלי.
וכאן בדיוק התחיל תפקידה של הפיזיקה, עם המדידות שלה.
וכאן בדיוק התעורר גל התנגדות גדול מצד המתמטיקאים, שאינם מוכנים להודות כי החישובים שלהם לא מתאימים לכל המעגלים, אלא רק למעגל שקוטרו מתקרב לאינסוף מ"מ.
האם אתה מכיר מתמטיקאי שיסכים להודות, כי הטיפול במעגלים לא שייך למתמטיקה ולחישובים שלה, אלא הוא שייך לפיזיקה ולמדידות שלה . אתה מכיר ????
אתה מבין למה לא מאמינים לתוצאות של ניסוי ההיקפן ? הרי מדובר ברעידת אדמה מתמטית, ובהתפרצות הר געש הנושא בשורה של גיאומטריה חדשה.
מה חשבת ? שיאמינו לי ? אני ידעתי שלא יאמינו לי , וגם ידעתי על התגובות הצפויות שידונו בבעל העניין, ולא ידונו בעניין עצמו.
כבר אמרתי וחזרתי, אם מוסד מדעי מכובד כמו הטכניון יחזור על ניסוי ההיקפן, הקהילה המדעית תקבל את פסיקתו. האם ניסוי חוזר שכזה מרתיע את האקדמיה ? כנראה שכן
דיברנו מספיק בנושא …הגיע עת המעשים….הוציאו קול קורא לאקדמיה של המדעים המדויקים.
אליהו
האם עצבר הוא טרחן כפייתי כדבריך שאינו מודע לכך, שרלטן במודע, או שאולי הוא בכלל צודק ופאי אכן קטן ביחס ישיר לקוטר המעגל?
בוא נבדוק:
עצבר, אתה מתנסח ברהיטות וניסוי ההיקפן שלך יפה ומרשים, מה שפוסל את האפשרות שאתה טמבל מושלם.
נקבל את טענתך שהיחס בין שני הגלילים בניסוי שלך הוא בדיוק 60:1. הראית בוידאו שכאשר מסובבים את ההיקפן, אנו מקבלים יחס שונה מ60:1 מה שלטענתך מוכיח שפאי של הגליל הקטן גדול מפאי של הגלגל הגדול.
אך לניסוי יש מרווח שגיאה גדול מדי, שניתן לתקנו בקלות עיי מספר סיבובים גדול יותר. הרי אם טענתך נכונה, אז אם תסובב את הגלגל פי 100 תקבל הפרש מרחק גדול פי 100, לא?
התואיל לבצע פעם נוספת את הניסוי ולצלם בוידאו עם מספר סיבובים גדול יותר? הציוד הרי נמצא ברשותך והניסוי לא צריך לארוך יותר מ20 דקות. אם תקבל הפרש גדל והולך ככל שמספר הסיבובים גדול יותר, לא יהיה ניתן לפסול את טענתך יותר, וכל אחד פה אני מאמין ישמח לשתף את הקהילה האקדמית במתמתיקה החדשה שלך.
האם תבצע זאת, עצבר? מה הם 20 דקות לעומת הנצח ותהילת הנצח?
אליהו וכולם, שימו לב שלפני עצבר עומדות כעת 3 אפשרויות, עם 3 תוצאות אפשריות:
1. עצבר יבצע את הניסוי עם 100 סיבובים (לא יותר משעה) או עם 10 סיבובים (10 דקות), יפרסם את הוידאו, ויוכיח לעולם את צדקתו. גאון!
2. הוא יבצע את הניסוי יווכח בטעות ויודה בה. קראקפוט, אבל ישר.
3. הוא יסרב לבצע את הניסוי ויאמר שהניסוי שביצע כבר מספיק. שרלטן.
וקיימת כמובן האפשרות הברורה מאליה שהוא כבר מזמן ביצע את הניסוי עם מספר סיבובים גבוה יותר ונוכח באיוולתו..
עצבר
לא הבנתי מהי "ההבחנה" – "…שהביאה לעולם גיאומטריה חדשה…"
אני מזכיר לך: הגיאומטריה שלך, אינה מבוססת על כל גודל או כוח פיזיקלי ידוע…
חלומות פז.
הטרחנים הכפייתיים המתמטיים, לפי דודליי, הם כמעט תמיד גברים, וכמעט תמיד מבוגרים, לרוב בשנים שלאחר הפרישה מעבודה. הם אינם מבינים מה משמעות הטענה המתמטית שדבר מסוים אינו אפשרי. הידע שלהם בתחום שבו הם פועלים חלקי ביותר, ובדרך כלל הם חסרי השכלה פורמלית. הם סבורים שהבעיות שהם תוקפים הן בעלות חשיבות רבה, ונוטים לחשוד שזכויות היוצרים ייגנבו מהם. מעל לכל, לא ניתן לשכנע אותם שהם טועים.
בשל חוסר ההכרה בתגליות שלהם, טרחנים כפייתיים טוענים במקרים רבים לקונספירציה לה שותף הממסד המדעי המתנכל להם ומתכחש בכוונה לאמת. טרחנים משתמשים במונחים שהומצאו על ידם שאין להם הגדרה ברורה ונמנעים משימוש במונחים ברורים ומוגדרים היטב. כשהם מתבקשים להסביר את מינוחיהם, הם נוטים לעשות זאת באמצעות מונחים מעורפלים באותה המידה.
פעמים רבות הבעיה הבסיסית בטענותיהם של טרחנים כפייתיים היא חוסר הבדלה בין הגדרות, עובדות ודעות. תוצאות הסותרות את האינטואיציה שלהם נפסלות על ידם, לכאורה על ידי נימוק ריגורוזי אולם למעשה פעמים רבות טיעונם מורכב מרבדים רבים של טענות והגדרות שבבסיסן אין עקביות או שהנימוק היסודי מתבסס על הנחה אינטואיטיבית.
טרחנים כפייתיים זה המונח הנכון למר עצבר
ראו כאן :
http://www.haayal.co.il/story_1571
וגם כאן:
https://he.wikipedia.org/wiki/%D7%98%D7%A8%D7%97%D7%9F_%D7%9B%D7%A4%D7%99%D7%99%D7%AA%D7%99
אין מה להתעצבן או לכעוס זוהי נכות נפשית כמו כל תסמונת נכות נפשית אחרת ויש להכיל אותה בהבנה וסובלנות
לאסי
ואם עוד לא השתכנעת היעזר במאמר הזה
http://img2.timg.co.il/forums/3/45317ede-eca8-48bc-8608-477e5a47c910.pdf
אם לא השתכנעת אסי, העזר במאמר הזה
http://img2.timg.co.il/forums/3/51ea21af-238b-4926-8045-06105f2e4ed6.pdf
לאסי
ריבוע גדול דומה לריבוע קטן, והם בעלי צורה זהה.
הביטוי המתמטי לצורה…הוא מספר יחס
לכן, היחס בין היקף כל ריבוע לאלכסונו הוא קבוע וערכו המקורב 2.8284342
קו עגול סגור גדול, לא דומה לקו עגול סגור קטן, ואין הם בעלי צורה זהה.
צייר בעזרת מחוגה קו עגול סגור שקוטרו 12 ס"מ, וקו עגול סגור שקוטרו 1.5 ס"מ
שים לב שלכל קו עגול סגור, יש צורה אחידה….אבל ייחודית
לקו עגול סגור שקוטרו 12 ס"מ , יש צורה אחידה, אבל ייחודית , (ובהכרח יש לו מספר יחס ייחודי).
לקו עגול סגור שקוטרו 1.5 ס"מ, יש צורה אחידה, אבל ייחודית, (ובהכרח יש לו מספר יחס ייחודי)
מדובר על היחס בין אורך ממשי של קו עגול סגור,,,לאורך הממשי של קוטרו
אורך ממשי מוצג עם מספר של מ"מ. ס"מ, מטר וכן הלאה.
זוהי ההבחנה שהביאה לעולם גיאומטריה חדשה, אבל המתמטיקה לא מסוגלת להביע אותה.
רק מדידה מדויקת מסוגלת להבחין בה, וניסוי ההיקפן הוא נושא הבשורה.
מדידה שייכת לפיזיקה, ולכן הגיאומטריה החדשה היא גיאומטריה פיזיקלית
הגיאומטריה העתיקה, של הקו הישר היא גיאומטריה מתמטית, הנשענת על חישובים המבוססים על משפט פיתגורס.
אל תמהר לפסול ולהציע לחסום .
אל תהסס להודות בטעות
בהצלחה
אם הפיי שלך משתנה, כנראה שהמעגלים שלך לא מושלמים אלא אליפסות.
אם אתה לא מסוגל להבין שמעגל זו צורה קבועה ולא משנה הגודל שלה, אז תחזור בבקשה לכיתה א
שמישהו יחסום את עצבר בבקשה.
מדובר בטרול מצוי שכל מטרתו לעורר דיונים עקרים על נושא שיש בו תמימות דעים מוחלטת. כבר אלפי שנים ואלפי פיתוחים נסמכים על כך שיש פיי קבוע.
כמו לטעון שהיחס בין היקף ריבוע לאורך הצלע שלו הוא לא 4\1 אלא משתנה.
די כבר ,
…1/9 +pi x 4 =1-1/3+1/5-1/7
אתה מבין מה כתוב כאן ?
המתמטיקאים מעולם לא חישבו את היחס בין היקף המעגל לקוטרו, מכיוון שאין במציאות חישוב כזה.
חישוב מתמטי מתאים רק לקטעי קו ישר, ואינו מתאים לקו עגול.
העיסוק בקווים עגולים סגורים שייך לפיזיקאים ולמדידות המדויקות שלהם , ואינו שייך למתמטיקאים ולחישובים שלהם.
גם בלי ניסוי מעשי, אפשר להוכיח את רעיון פאי המשתנה
http://img2.timg.co.il/forums/2/5604aa4e-34d1-49c7-86a2-4905ab2f0392.pdf
טוב , נגיד שנזרום עם גיבוב השטויות שלך,
תגיד, אתה מודע לזה שמדדו את פיי עשרות ספרות אחרי הנקודה ? בעשרות דרכים שונות ?
-אתה מודע לזה שאפשר לקבל את פיי גם כסכום של סדרה אינסופית ?
-אתה מבין שהדיוק היחסי של הניסויי ההזוי שאתה מציע, מוגבל בשגיאה שלו, לשגיאה המדידה בחריטה של 2 מ"מ הרדיוס /היקף של הגליל הפנימי ? (שזה בערך 20 מיקרון לרדיוס במקרה הטוב,וכנראה הרבה יותר גרוע להיקף ) וזה גורר שגיאה הרבה יותר גדולה מהאפקט 0.995 שאתה טוען לגביו ?
אני מעריך שמספר הקוראים שהצלחת לשכנע עד עכשיו עם השטויות שלך הוא בערך 1 עד 2 כולל אותך.
בעולם המבוגרים , יש משהו שנקרא מאמר מדעי. ויש משהו שנקרא peer review. למרות שלא שנראה לי שתמצא חוקר כלשהו שירצה ויצליח לקרוא את השטויות האלו ? אולי תמורת תשלום נאות …
האמת שהתגובות שלך הן ממש מרתקות,
אבל יותר מתאימות למדור הכתבות בנושא פסיכולוגיה קלינית , תחת הנושא שגעון גדלות.
אבל אל תתן לכל זה לייאש אותך ..
https://www.sciencealert.com/a-tiny-muon-s-wobble-could-break-physics-as-we-know-it
והנה מחקר (בהמשך הכתבה) שמראה שהחישוב התיאורטי לא נכון ומראה שתוצאות הניסוי מתאימות לחישוב המתוקן
החקירה העתיקה של המציאות הפיזיקלית, עסקה "בכל מה שהוא נתפס בחושים , והעניקה לו את השם חומר. ניוטון קבע שהחומר הוא מושג כמותי, ואפשר למדוד את משקלו.
אבל החומר אינו מושג כמותי, והוא בגדר של צורה פיזיקלית.
תפיסה זו יוצרת פיזיקה חדשה לחלוטין, ומבטלת את תפיסתו החלקיקית של החומר.
הנה היא התפיסה הישנה
https://he.wikipedia.org/wiki/%D7%97%D7%95%D7%9E%D7%A8_(%D7%A4%D7%99%D7%9C%D7%95%D7%A1%D7%95%D7%A4%D7%99%D7%94)
אולי זה נשמע לך כך, אבל זה מדעי , כמותי , ונמדד
עצבר, זה נשמע כמו ציטוטים מתורת הקבלה
ואם עורכי הניסוי אכן יחזרו על ניסוי ההיקפן, הם גם יגלו לעולם את קיומה של אסטרופיזיקה חדשה .
http://img2.timg.co.il/forums/2/ac193a50-8b58-4711-89bd-475f16879d2a.pdf
אני מציע לעורכי הניסוי הזה לחזור על ניסוי ההיקפן, ולגלות לעולם שיש גיאומטריה חדשה, שבאמצעותה ניתן להציג פיזיקה חדשה.
https://youtu.be/HY7GQxU1HLk
מיואון נבחר כי הוא חלקיק יסודי דומה מאוד לאלקטרון אבל כבד יחסית ולכן מגיב באופן עוצמתי יותר לחלקיקים בטבע. מעבר לכך יותר קל לייצר אותו ביחס לשאר החלקיקים (מלבד האלקטרון שאת המומנט המגנטי שלו כבר מדדנו). הרעשים בוואקום, שהם חלקיקים שנוצרים ונעלמים ברגע, משפיעים על איך המגנט הפנימי של המיואון מסתובב. אם התאוריה לא תואמת את המדידות סביר להניח שקיים משהו נוסף שתורם לאיך המגנט של המיואון מסתובב. כמובן שיכול להיות שמשהו שכבר ידוע לנו לא עובד כמו שאנחנו מצפים אבל נערכו כבר כל כך הרבה ניסויים על המודל הסטנדרטי שקשה להאמין שמשהו במודל עצמו שידוע כבר לא נכון.
למה דווקא מיואון?
ועל מה מדובר בכלל? שקיים משהו שמפריע (או מתערב) בשדה מגנטי של מיואון?
(יש כאן באתר אנשים מקצועיים שגם מגיבים? או שזה רק עצבר? כי אם זה רק עצבר אז אלוהים יודע איך האתר הזה שורד בכלל).
הפיזיקה החדשה היא פיזיקה גיאומטרית, ורעיון החלקיקים הגיע לסוף דרכו
פיזיקה גיאומטרית
קו הוא המושג היסודי של הגיאומטריה, ויש לו שני נתונים
נתון ראשון – אורך ממשי נתון שני – צורה
אנרגיה היא המושג היסודי של הפיזיקה, ויש לה שני נתונים
כמות ממשית – וצורה ( מכנית, תרמית, חשמלית, כימית וכו')
אנרגיה יכולה לשנות צורה, אבל הכמות הממשית תמיד נשמרת.
למושג הצורה יש חשיבות עליונה
גוש בצק הוא תמיד בעל צורה.
צורתו של גוש בצק נובעת מצירוף כמויות של שני דברים אחרים.
נפח ושטח הם שני דברים כמותיים – אבל נפח הוא דבר אחר משטח
צורתו של גוש בצק נובעת מצירוף כמויות של נפח הגוש ושטח פניו.
מעיכת גוש הבצק משנה את כמות שטח פניו, אך נפחו נשאר קבוע.
לכן, מעיכת גוש הבצק משנה את צירוף הכמויות של נפח ושטח פנים, ובעקבות שינוי זה מתחולל שינוי צורה של גוש הבצק.
צורה גיאומטרית סגורה במישור נובעת מצירוף כמויות של היקף המכיל שטח.
היקף ושטח הם שני דברים כמותיים אחרים.
צורת הריבוע נובעת מצירוף כמויות מסוים, של היקף המכיל שטח.
צורת המעגל נובעת מצירוף כמויות מסוים של היקף המכיל שטח
וכמו שיש צורה גיאומטרית, כך יש גם צורה פיזיקלית
גם צורה פיזיקלית נובעת מצירוף כמויות של שני דברים אחרים.
צורה פיזיקלית נובעת מצירוף כמויות של אנרגיה וזמן פסיבי.
זמן פסיבי הוא מושג יסודי של הפיזיקה החדשה.
זמן פסיבי הוא נח מוחלט וקר מוחלט, והוא ממלא את המרחב האינסופי.
זמן פסיבי הוא התווך המעביר את אור השמש.
הכוכבים נעים דרך הזמן הפסיבי, והוא לא מפריע לתנועתם.
זמן פסיבי קיים במציאות הפיזיקלית, ואילו הזמן האקטיבי המוכר לכולנו קיים רק בתודעת האדם.
החומר הוא בגדר של צורה פיזיקלית, ואינו מושג כמותי.
החומר נוצר מצירוף כמויות של זמן פסיבי ואנרגיה
לכן, מד חומר לא קיים , ולעומת זאת מד אנרגיה כן קיים , ומד זמן פסיבי כן קיים.
והיות שהחומר הוא צורה פיזיקלית, אין מקום לתיאוריה חלקיקית של החומר.
גיאומטריה פיזיקלית ופיזיקה גיאומטרית שלובות זו בזו.
גיאומטריה פיזיקלית מכילה רמזים על המציאות הפיזיקלית האמיתית.
השערה
המספר 1.007 יופיע בגיאומטריה פיזיקלית, וגם בפיזיקה גיאומטרית.
בגיאומטריה פיזיקלית הוא מביע את היחס בין מספרי המעבר הקיצוניים
3.1416 ו 3.164
בפיזיקה גיאומטרית הוא מביע את קיומו של תחום מהירויות צר , הקשור
למבנה היקום. היחס בין המהירות הגבוהה של התחום, למהירות הנמוכה של התחום הוא 1.007
המשך יבוא
א.עצבר
4/2021