בשתי הגרלות לוטו שונות עלו בגורל אותם מספרים בדיוק. הגם שמדובר בסיפור משעשע, הדיווחים בתקשורת כאילו לפנינו מאורע בהסתברות של אחד לטריליונים – מופרכים לחלוטין

דני הלמן
בשתי הגרלות סמוכות למדי של מפעל הפיס, הראשונה ביום שלישי, 21 בספטמבר, והשנייה במוצאי השבת, 16 באוקטובר, עלו בגורל אותם שישה מספרים בדיוק: 13, 14, 26, 32, 33 ו-36. במהדורה המרכזית של ערוץ 10 דווח למחרת כי ההסתברות להתרחשות שכזו קטנה מאחד לחמישה טריליון (חמש ואחריו 12 אפסים). באתר YNET יוחס למאורע הערך ההסתברותי 0.00000000000025. בעיתונים "הארץ" ו"ידיעות אחרונות" נכתב כי הסיכוי שאותם שישה מספרים יעלו בגורל פעמיים בתוך חודש הוא 1 ל-4 טריליון. גם אם נסכים כי מדובר בצירוף מקרים מעניין למדי, יש להבהיר כי אומדני חוסר הסבירות הללו הם חסרי כל שחר!
בהגרלת הלוטו של מפעל הפיס הנהוגה כיום יש לנחש שישה מספרים שונים בטווח 1 עד 37. מספר ההרכבים האפשריים הוא שניים וחצי מיליון בקירוב (2,324,784). בהתאם לכך, הסיכוי של כל שישיית מספרים שהיא, לרבות ההרכב הזוכה מההגרלה הקודמת, לעלות בגורל בהגרלה הבאה הוא בסביבות אחד לשניים וחצי מיליון. תחת ההנחה של הגרלה הוגנת, ההסתברות לחזרה על אותם שישה מספרים בדיוק, בשתי הגרלות עוקבות, אינה אלא זו: אחד לשניים וחצי מיליון בקירוב.
זאת ועוד, במקרה הנוכחי לא מדובר באמת בשתי הגרלות עוקבות, אלא בשתי הגרלות בטווח של כחודש זו מזו. מפעל הפיס עורך בחודש אחד כעשר הגרלות לוטו. הסיכוי שבמהלך עשר הגרלות שונות תהיה חזרה על אותו הרכב של שישה מספרים זוכים הוא אחד לחמישים אלף בקירוב (1/51,662). יש להביא בחשבון כי צמד הגרלות מהווה הזדמנות אחת ויחידה להתאמה, אולם בקרב קבוצה של עשר הגרלות כלולים 45 זוגות להתאמה פוטנציאלית.
שאלה של הגדרה
כיצד אפשר להסביר את הפער העצום בין ערכי ההסתברות האמיתיים ובין ערכי ההסתברות המוגזמים שבהם נקבו כלי התקשורת? מקור עיקרי לטעויות מסוג זה הוא אי התאמה בין המאורע שאת סיכוייו מבקשים לאמוד ובין המאורע שאת סיכוייו מחשבים בפועל. כדי להימנע מן השגיאה יש לשים לב מה היא בדיוק ההתרחשות לגביה שואלים, ולהתאים את התחשיב ללשון ההגדרה.
ההסתברות ששישיית מספרים מסוימת (למשל 1-2-3-4-5-6) תעלה בגורל בהגרלה בודדת היא בסביבות 1 לשניים וחצי מיליון, ובשתי הגרלות רצופות בסביבות 1 לחמישה וחצי טריליון. ואולם ההסתברות ששישיית מספרים כלשהי תעלה בגורל בהגרלה בודדת היא 1 (וודאי שהרכב כלשהו יעלה בגורל), ובשתי הגרלות רצופות – בסביבות 1 לשניים וחצי מיליון. היות שהמאורע שעורר את ההד התקשורתי הוא עצם החזרה על אותו הרכב של שישה מספרים, ולא החזרה על הרכב מסוים של שישה מספרים, הרי שכל שישיית מספרים שהיא – ולאו דווקא זו שעלתה בגורל בפועל – היתה יכולה להתאים להגדרת המאורע.
השאלה איננה מה ההסתברות שההרכב 36-33-32-26-14-13 יעלה בגורל בשתי הגרלות, שאז התשובה היא אכן פחות מאחד לחמישה טריליון, אלא מה ההסתברות שהרכב כלשהו מבין שניים וחצי מיליון ההרכבים האפשריים יעלה בגורל בשתי הגרלות, שאז הסיכוי גבוה פי שניים וחצי מיליון.
כסף קטן
א. על מנת לזכות בפרס הגדול בלוטו על המשתתף לנחש נכונה את הרכב ששת המספרים הזוכים מהתחום 1-37, וכמו כן מספר אחד נוסף ("המספר החזק") מהתחום 1-8. המספר החזק שעלה בגורל בשתי ההגרלות הנדונות לא היה זהה. אולם לטובת המאמינים (מכל הזרמים) אפשר לציין כי בהגרלה הראשונה מבין השתיים עלה בגורל, בתור המספר החזק, המספר 1, ובהגרלה השנייה – המספר 2.
ב. מספר ההרכבים האפשריים של שישה מספרים שונים מהטווח 1 עד 37:
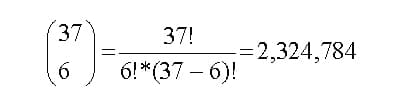
ג. ההסתברות לחזרה על אותו הרכב של שישה מספרים זוכים במהלך עשר הגרלות:
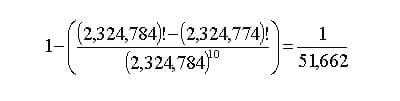
דני הלמן, המחלקה לפסיכולוגיה, אוניברסיטת תל-אביב

14 תגובות
עובדים עליכם כל יום.
כל העסק הזה מריח לא טוב.
אולי פעם עוד נזכה לשמוע איך עבדו עלינו ,חוסך כספו שירחק מהמפעל המפואר הזה.
יואל: שכחת שצריך למלא גם מספר חזק בין 1-10, כלומר, הסיכוי לזכות בפרס הראשון בלוטו הוא 1 ל-2.5 מליון לערך כפול 10 אפשרויות של המספר החזק. הווה אומר, 1 לכ-25 מליון.
על פניו התחשיב [סיכוי של 1 ל-2.5 מליון ] אינו נכון. ראשית כי מספר הניחושים הנכונים הוא פחות מאחד ל-5 הגרלות ועפ"י הנתונים הכספיים של מפעל הפייס אני מבין שמספר הטורים הממולאים בכל הגרלה בודדת עובר את הממוצע של 3 מליון מה שהיה מצריך ממוצע של מצליח כל מחזור.
בנוסף עלות כל טור היא פחות מ-2.8 ש"ח X האפשרויות =7 מליון ש"ח . כשפרס ראשון התחלתי הוא 5 מלש"ח אין סיכוי להרוויח ומפעל הפיס גם לא הדיוט ובאופן כללי נוהג להרוויח,כמה מוזר.
אז במקום שאני אגרד את התאים האפורים בכזית מח שלי אולי למאן דהו תחשיב עדכני
מקריות או לא, זאת לא היתה פעם ראשונה שאותם מספרים חוזרים.
ב16.10 חזרו אותן שישיות בלוטו
ב27.10 חזרו אותם מספרים בפיס 123
16.02.2011 חזרו אותם 4 קלפי צאנס הגרלה אחרי הגרלה!
אני עוקב אחרי הגרלות הפיס וכל החזרות היו בטווח קצר של תאריכים,וזה לא קרה בשנים קודמות.
אומנם הסיכוי שיהיו חזרות 6 מספרים הוא 1:2 מיליון,אבל חזרו אותם מספרים באותם מקומות,האם לא כדאי לעשות חישוב עם חשיבות למיקום?
הסיכוי הרבה פחות גבוה אם מתיחסים לשאלה מה הסיכוי שארוע כז או דומה יקרה אי פעם מזמן הקמת מפעל הפייס הסיכוי עולה אחרי כל חודש שעובר וגם אם היה הפרש של 12 הגרלות בין הארועים גם הסיכוי היה עולה.
מה הסיכוי שארוע זה היה קורה בצורה טיבעית בכל שנות מפעל הפייס התשובה בערך 1%
בקיצור לא סביר
Brilliant!
גם אם אתה מהמר על מס' אחד שכבר היה הסיכוי יהיה אחד ל-2 מיליון (2.5?)
אבל פה מדובר על זה שיש 45 אפשרויות לזוגות, לכן זה כאילו שאתה קונה 45 טפסי הרשמה שונים ללוטו על מנת לזכות.
שלומי הלינק שכתבתה לא עובד
האם רק לי יש הרגשה שמישהו צוחק עכשיו על כל הסטטיסטיקה והחישובים? ברור שאם אתה שולט בהגרלה הסיכוי הוא 1 , לא?
איפה כל הקונספירטורים כשבאמת צריכים אותם?
הסבר מעט יותר אינטואיטיבי לתוצאה האחרונה:
הסיכוי לזכות בלוטו הוא x. לכן אם עושים 10 הגרלות אזי לאחר ההגרלה הראשונה, הסיכוי שייצא x באחת משאר 9 ההגרלות שנותרו הוא x*9 (זה לא מדוייק לחלוטין אך מכיוון שx הוא קטן מאוד אז זה די מדוייק). לאחר ההגרלה השניה הסיכוי שx ייצא בשאר ההגרלות שנותרו הוא 8x וכן הלאה.
ולכן מקבלים שהסיכוי שיקרה אותו מאורע שהסיכויוי שלו הוא x פעמיים בתוך 10 הגרלות הוא
0+1+2+3+4+5+6+7+8+9=45*x
2324784/45=51662
הידד להסתברות!
כתבתי על כך באתר של מכון ויצמן:
http://www.weizmann.ac.il/zemed/net_activities.php?cat=1415&incat=1412&article_id=3672&act=forumPrint
אז מה זה אומר ?
שעדיף למלא מספרים שהיו כבר? (הסיכוי הוא 1 ל 50000 במקום 2 מיליון!!)
זה לא הגיוני כי לסטטיסטיקה אין זיכרון