המודל הסטנדרטי ומעבר – כל מה שצריכים לדעת

זאת הייתה אחת מההצלחות המדעיות הגדולות של המאה העשרים, יש שיגידו שזו הייתה המשימה החשובה ביותר במדע. המשימה טרם הושלמה ואולי גם לא תושלם לעולם. מהו המודל הסטנדרטי? ומה מסתתר מעברו? כתבת עומק מיוחדת לחג – תקציר היסטורי, משמעויות ומחשבות להמשך 

את המודל הסטנדרטי אי אפשר להכיל בכתבה אחת אבל את עיקריה ראוי לסכם. אפשר להתווכח מתי לראשונה צמח המודל הסטנדרטי, אך ניתן לומר בבירור שהמודל התחיל עוד לפני שבכלל ידעו על קיומו. בשנת 1896, כשההתלהבות מגילוי קרינת הרנטגן הייתה בשיאה, הפיזיקאי אנרי ברקל גילה לראשונה את הרדיואקטיביות כשהצמיד מלחי אורניום מול דפי צילום.

באותם ימים לא ידעו דבר על חלקיקים (היו השערות על קיומם) ולאנרי לא היה הסבר פיזיקאלי משכנע. שנה מאוחר יותר החלקיק היסודי הראשון, האלקטרון, התגלה על ידי תומסון בעזרת שפורפרת קרן קתודית. בתקופה זו המושג “חלקיק” היה שנוי במחלוקת ולפיזיקאים לקח זמן רב עד שקיבלו את העובדה שכולנו עשויים מאטומים. השאלה “ממה אנחנו עשויים?” הציתה את דמיונם של המדענים ולמרות הקושי דחפה אותם להציע השערות. הראשון לתת מודל לאטום היה תומסון שהציע את מודל “עוגת הצימוקים” – כדור טעון חיובית עם “צימוקים” של חלקיקים הטעונים שלילית. כדי לבחון את השערתו, רתרפורד הפגיז על רדיד זהב חלקיקים טעונים וצפה בהתפזרותם. בעזרת תמונת הפיזור נבנה מודל חדש שהסביר את מבנה האטום – גרעין טעון חיובית כמסביבו חגים חלקיקים טעונים שלילית בדומה מערכת השמש. כחיזוק למודל, רתרפורד גילה גם את הפרוטון בשנת 1919. בין לבין, איינשטיין ייסד את תורת היחסות והספיק לפרסם הסבר תיאורטי לתנועה בראונית שלימים הפכה להוכחה הראשונה לקיומם של אטומים.

תגליות משמעותיות מצריכות הסבר תיאורטי מעמיק ולתוך הוואקום צמחה תורת הקוונטים. הראשון לחשוף את תכונותיה המפליאות של מכניקת הקוונטים היה מקס פלאנק כשפתר את ה”קטסטרופה האולטרא-סגולה”. “הקטסטרופה”, כפי שכונתה, סתרה את חוק שימור האנרגיה. כל גוף חם פולט קרינה במגוון תדרים ועוצמת הקרינה בכל תדר תלויה בטמפרטורה. הפיזיקה של אותם ימים כשלה מלהסביר את העוצמת הקרינה בטווח התדרים של אור אולטרא סגול ומעלה. נראה שכמות האנרגיה באיזור

זה הולכת וגדלה עד אינסוף כשבפועל היא הולכת וקטנה. כדי לפתור את הבעיה, הציע פלאק את ההשערה שאנרגיית האור מגיעה במנות קטנות. חשוב להדגיש עד כמה מהפכני היה הרעיון של פלאנק – עד לתקופתו מרבית הפיזיקה, אם לא כולה, התבססה על מתמטיקה רציפה. לטעון שהאור קיים במנות ולהשתמש במתמטיקה בדידה לפיתרון בעיה פיזיקאלית היה בהחלט מהפכני. כדי להסביר את האפקט הפוטואלקטרי אינשטיין השתמש ברעיון של פלאנק שהתאימה לו כמו כפפה ליד. התכונה החלקיקית של האור קיבלה אישוש נוסף – האלקטרון שב למרכז הבמה כשקומפטון הסביר את תופעת הפיזור בין אלקטרון ופוטון (השם שניתן לחלקיק האור). בזכות עבודתם של כמה מהפיזיקאים הגדולים של המאה ה- 20, ניתן לומר שתורת הקוונטים קיבלה חיים משלה והגיעה לשיאה כששרדינגר פירסם את משוואתו בשנת 1926. משוואת שרדינגר מתארת את ההתפתחות הזמנית של פונקציית הגל כתלות באנרגיה.

זו הייתה אבן דרך במכניקת הקוונטים. רבים מקוראי המדע הפופולארי שוגים בטענתם כשאומרים שפונקציית הגל מרמזת שמכניקת הקוונטים אינה דטרמיניסטית. אך מה דטרמיניסטי ומה לא? פונקציית הגל מייצגת תכונה הסתברותית לערכים מדידים, כמו למשל מיקומו או מהירותו של חלקיק. כל עוד החלקיק לא נצפה (שזו גם תכונה שאין עליה ממש הגדרה משביעה רצון), מיקומו לא נקבע. אומנם הבחירה של החלקיק להימצא במיקום מסוים איננה דטרמיניסטית, פונקציית הגל ומשוואת שרדינגר שמפתחת אותה בזמן דטרמיניסטית לחלוטין. בכל רגע ניתן לדעת במדויק מה ההסתברות למציאת החלקיק. כשהמשוואה דטרמיניסטית אנו אומרים שגם התורה כזו. דוגמא נגדית לכך היא תנועה בראונית. המשוואה של איינשטיין לתנועה זו אינה דטרמיניסטית כי היא מכילה בתוכה חלק רנדומי.

המשוואות של מקסוול

כאן צריך לעצור לרגע ולחזור מספר שנים אחורה אל העידן של מקסוול. ג’יימס מקסוול היה חוקר מחונן וידיד קרוב של פאראדיי. עם אינטואיציה חדה ודימיון פורה פאראדיי תיאר מרחב מסתורי שממלא את החלל ולו הוא נתן את השם “השדה החשמלי והמגנטי”. למרות האינטואיציה המופלאה והיותו נסיין מחונן, הוא לא הצליח להסביר מתמטית את התופעות החשמליות והמגנטיות במלואן. כאן בא לעזרתו מקסוול, שכתב באופן אלגנטי את משוואות התורה האלקטרומגנטית. באמצעות משוואות אלו הוא הראה שהאור למעשה מורכב מגלים בשדה האלקטרומגנטי. גם כאן מופיעה מהפכה מחשבתית בפיזיקה. אובייקט מסתורי שלא נראה בעין האנושית ממלא את החלל ותנודות בו יוצרות את מה שאנחנו מכנים כאור. זה נשמע בהחלט מופרך לכל אחד מאיתנו, אבל הטבע לא עובד על בסיס ההגיון האנושי.

זו הייתה נקודת הפתיחה לתורת השדות. לפנינו שתי תאוריות שמתארות את האור אך שונות במהותן. כיצד הן משתלבות? האם אחת היא השתקפות של השנייה? מצד אחד האור מתואר כחלקיק, מצד שני הוא גל בשדה האלקטרומגנטי, מה נכון? במרחק של כמה שנים ובעזרת תחכום מתמטי הצליחו הפיזיקאים לשלב בין השניים. הפיזיקאים “קווינטטו” את השדה וקיבלו את התכונות החלקיקיות. כשפיזיקאים אומרים “קווינטוט” הם מתכוונים שהשפה המתמטית מתבססת על עקרונות תורת הקוונטים. בפועל השפה המתמטית מאפשרת למדענים ליצור גלים בשדה כשכל גל מייצג חלקיק עם אנרגיה בהתאם לתדר. אחד מהמדענים הראשונים שעשה שימוש בשפה החדשה-ישנה היה פרמי. בשנות העשרים של המאה הקודמת פיזיקאים גילו תופעה גרעינית ייחודית בזמנם- התפרקות בטא. התפרקות זו קיבלה תיאור פיזיקאלי בשנות השלושים שנתיים אחרי שהייזנברג הציע את קיומו של הנייטרון. בהתפרקות בטא הנייטרון מתפרק לפרוטון, אנטי – אלקטרון ונייטרינו (שאז קיומו היה רק משוער). פרמי ניסח הכל באופן מתמטי וכתב את ה”לגראנג’יאן” של התורה. הלגראנג’יאן הוא ביטוי מתמטי חשוב בפיזיקה כי הוא גולל בתוכו את התורה עצמה. זהו ביטוי שנלקח ממכניקה קלאסית שאיפשר לפיזיקאים למצוא את משוואות התנועה בלי השפה המסורבלת של ניוטון. משוואות התנועה מספרות על התפתחות המערכת ובאמצעותן ניתן לחקור את הטבע. היו לא מעט ניסיונות מוצלחים יותר או פחות בכתיבת הלגראנג’יאן, ובאמצעות ניסוי, טעייה, ואימות תצפיתי השפה המתמטית נבניתה.

בסוף שנות הארבעים הניסיון לשלב בין התאוריות מסתיים בהצלחה מרובה. האיחוד בין תורת השדות ומכניקת הקוונטים נצפו בדיארגמות יפייפיות ובלגראנג’יאן אלגנטי. בעזרת דיאגרמות פיינמן המפורסמות, ניתן לתאר ולחשב כל תהליך פיזיקאלי המערב חלקיקים טעונים ופוטונים (בהמשך דיאגרמות פיינמן השתלבו בכוחות נוספים). אין זה אומר שהחישוב פשוט, אך כעת ברור יותר אילו ביטוים עולים על הנייר. בפיזיקה, לא תמיד ניתן לחשב תהליכים במדויק ולכן משתמשים בשיטה “פרטובטיבית”, כלומר שיטות לקירוב.

לעיתים לספרה הרביעית (למשל) אחרי הנקודה העשרונית אין משמעות כי אף פעם לא ניתן למדוד במדויק. הרי לכל מכשיר מדידה קיים טווח רגישות שמעברו הוא כבר מפסיק להיות אמין. התורה הקוונטית לא תמיד מאפשרת לחשב תהליכים פיזיקאליים במדויק ולשם כך דיאגרמות פיינמן קיימות. אם הדיאגרמה נראית מסובכת, סביר להניח שהיא קיימת כדי לחשב  ספרה רחוקה אחרי הנקודה. ככל שמוסיפים לחישוב דיאגרמות שהולכות ומסתבכות, כך מידת הדיוק גדלה. אחת מההצלחות הגדולות של התורה היה החישוב המומנט המגנטי של האלקטרון (שהוא מאין מגנט פנימי כתוצאה מהספין). תצפיות עדכניות מראות התאמה מלאה עד הספרה ה-13 אחרי הנקודה העשרונית בין ניסוי לחישוב בעזרת דיאגרמות פיינמן. התאמה מושלמת כזו לא נחזתה מעולם.

לפתע בשנות החמישים פיזיקאים מגלים מגוון עצום של חלקיקים נוספים. בעולמנו כבר לא היו רק הפרוטונים, הנייטרונים, האלקטרונים והפוטונים, אלא חלקיקים עם שמות מוזרים כמו סיגמא, אטא, פאי, קאפא, למדא ועוד רבים (השמות כמובן נתנו “במקוריות רבה”  ולא תויגו סתם כך מתוך הטבע. לשמות כפי שאתם מבינים אין ממש משמעות). חלקם היו טעונים חשמלית ונפרשו על מגוון רחב של מסות. רבים מהם התגלו מהקרינה הקוסמית שבחלל אבל חלקם גם במאיצים שנבנו. מספר חלקיקים גילו תופעות מוזרות כמו התפרקויות בזמנים לא אופייניים ולכן קראו להם “מוזרים” (כשלימים נודע שאותם חלקיקים בנויים מקווארק בשם “מוזר”). פרסי נובל נמסרו כמעט לכל אחד שגילה חלקיק חדש עד שכבר נזרקה לאוויר האמירה שפרס נובל הבא צריך להגיע למישהו שלא גילה חלקיק. כאן התחיל המסע המופלא לחיפוש אחר תאוריה מאחדת. “גן החיות” החלקיקי נראה לפיזיקאים דבר “לא טבעי”. איך זה שכל כך הרבה חלקיקים קיימים? היכן האלגנטיות שראו בתורה האלקטרומגנטית? אחרי ההצלחה הגדולה של דיראק ופיינמן מדענים ניסו לחתור לכיוונם. מהו הלגראנג’יאן שמתאר את הכל? האם הוא בכלל קיים?

אז איך בכלל כותבים תאוריה להכל? ראשית צריך להבין את כללי המשחק של הטבע. עד לנקודת זמן זו הכלל היחיד שבאופן גורף התקיים עבור כל החלקיקים בטבע היה שימור תחת “טרנספורמציית לורנץ”. טרנספורמציה זו טבועה גם ביחסות פרטית של איינשטיין. היא מערבבת את הזמן והמרחב או את האנרגיה והתנע ליישות אחת. כמובן שהקשר העמוק בין הפרטים מופיע ביחסות כללית אבל יש לומר שהפיזיקאים התחילו “בקטן”. בשנות החמישים נכנס כלל נוסף שנקרא “רנורמליזציה”. זוהי שיטה מתמטית שמאפשרת לרשום את הלגראנג’יאן קצת אחרת כדי שממנו נוכל לערוך חישובים ולא לקבל דברים חסרי משמעות. לא תמיד ניתן להשתמש בשיטה זו ובמידה ויש לנו לגראנג’יאן שאינו “רינורמזבילי” (כלומר שלא ניתן לכתוב אותו ככזה שניתן לעשות עליו חישובים) התאוריה צריכה להישלח לפח כי היא לא פתירה (לפחות כרגע, אולי בעתיד יתגלה גאון שימצא שיטה חדשה).

כלל נוסף הגיע בשנות השישים על ידי הפיזיקאי היהודי גל-מן יחד עם גילוי הקווארקים. ובכן זה לא מדויק, יותר נכון לומר שהושלם על ידו. לשם כך צריך לחזור קצת אחורה בזמן. ב-1915 הפיזיקאית (היהודייה גם כן) אמי נתר כתבה בעבודתה הראשונה אחרי הדוקטורט את אחד מהמשפטים החשובים בפיזיקה עד היום – משפט נתר המקשר בין סימטריות לחוקי שימור. המשפט מראה שעבור מערכת פיזיקלית המקיימת סימטריה לטרנספורמציה מתגלה חוק שימור ולהיפך. לדוגמא, אם הפיזיקה לא משתנה כאשר מסיחים את מיקום החלקיק, התנע במערכת נשמר. אם הפיזיקה לא משתנה בזמן מתקיים שימור אנרגיה, ואם היא נשארת תחת סיבוב מתקיים שימור תנע זוויתי. אלו הם השימורים הקלאסיים שקיימים בטבע. כשאני טוען בדבריי “שהפיזיקה לא משתנה” הכוונה שתחת שינוי כלשהו (הזזה, סיבוב, מתיחה וכו’) של הקואורדינטות, הלגראנג’יאן שמתאר את הפיזיקה במערכת נשאר זהה (יותר נכון הפעולה אבל אין באמת סיבה לסבך את הקורא בעוד ביטוי מתמטי). אם הלגראנג’יאן לא תלוי בזמן למשל אז האנרגיה במערכת נשמרת.

כבר בתקופתו של דיראק ידעו שהלגראנג’יאן שמתאר את התורה האלקטרומגנטית מכיל סימטריה מעניינת, “סימטריית כיול”. זוהי סימטריה שמזכירה קצת סיבוב אבל היא על המישור המרוכב. הסיבוב המיוחד של השדה במרחב גורר שימור חדש – ואפשר כבר להניח שהבנתם כי מדובר בשימור מטען.

בחזרה לגל-מן. גן החיות החלקיקי רמז לגל-מן שעשויה להיות תבנית מסודרת יותר לטבע. אחרי לא מעט ניסיונות הוא סידר את החלקיקים שהתגלו לקבוצות בהתאם לתכונותיהם הפנימיות כמו ספין, מטען ו”איזוספין” (שלא אכנס אליו כעת, אך רק אציין שהוא קשור באופן אינטימי למטען החשמלי והועלה לראשונה כדי להסביר את הסימטריה בין הפרוטון והנייטרון).

התבנית שהתגלתה הייתה מופלאה כי היא הזכירה מבנה מתמטי מתורת החבורות. משום שהמבנה היה מורכב ולא יסודי, גל מן שיער שקיימים חלקיקים חדשים שתחת סידור זהה יחשפו את התבנית החברותית היסודית. תחת חיבור החלקיקים המשוערים, שכינה אותם בתור קווארקים, ניתן לחזור לתבנית המורכבת. את השם אגב גל-מן שאב מספרו של ג’יימס ג’וייס, גם כי אהב את השם וגם כי במשפט הופיעו שלושה ברווזים ממש כמו שלושת הקווארקים שגילה. המבנה החבורתי של הקווארקים מבטא סימטריה חדשה בטבע שלימים התגלגלה לסימטריה של הכוחות החלשים והחזקים.

עקרון הסימטריה

כאן הונחה עוד אבן דרך מרכזית במודל. באמצעות עקרונות פשוטים של סימטריה (שכוללת בתוכה את הדרישה לשימור הלגראנג’יאן תחת טרנספורמציית לורנץ) ורינורמליזציה ניתן לרשום את התיאוריה הכללית ביותר שעשויה להסביר את הטבע. גילוי הקווארקים איפשר למדענים לעשות סדר בגן החיות החלקיקי ולתאר בעזרת שישה אלמנטים פשוטים את המבנה הפנימי של כל החלקיקים שנצפו. במקביל לתאוריה של גל-מן ובאופן בלתי תלוי השתמש הפיזיקאי הישראלי, יובל נאמן, בעקרונות הסימטריה כדי לחזות חלקיק חדש שלא נצפה בגן החיות החלקיקי ואכן הוא התגלה בניסוי.

סוף סוף נראה שהמודל קרוב לשלמות אבל עם אופטימיות גדולה צצה בעיה לא קטנה. התאוריה החלקיקית שלנו חסרת מסה. מסתבר שאם מוסיפים לחלקיקים מסה באופן נאיבי אך מפורש, התאוריה לא רנורמזבילית יותר, משמע, לא פתירה. אנחנו יכולים לנסח תאוריה יפה כמה שנרצה אבל אם אין לה שום אחיזה במציאות היא לא שווה פרוטה. האם זה מוכיח שהניסיון כשל? לשם כך היגס (ובסיוע שתי קולגות) פיתח מנגנון חדש שאיפשר לחלקיקים בטבע לקבל מסה, אבל למנגנון הזה יש מחיר – חייבים להוסיף חלקיק נוסף כדי שיעבוד. ברמה המתמטית המנגנון עובד על ידי “שבירה ספונטנית של סימטריה”.

בלי להיכנס יותר מידי לפרטים, המנגנון יוצר אינטראקציה בין חלקיק ההיגס החדש עם חלקיקי הטבע הידועים. תחת אינטרקציה זו מתגלות המסות בטבע. חלקיק ההיגס, הידוע בכינויו “החלקיק האלוהי” התגלה רק בשנת 2012 במאיץ הגדול בסרן, ואם הוא לא היה נגלה זו הייתה יכולה להיות נקודת השפל הגדולה ביותר של התאוריה (השם ד”א פוצץ תקשורתית ונלקח למחוזות מתעתעים כשאין לו כמובן שום אחיזה במציאות. מי שהמציא את השם היה הפיזיקאי זוכה הנובל לנדרמן שכשהחלקיק האלוהי היה בכותרת ספרו. השם במקור היה החלקיק החמקמק (the goddam particle) אבל העורך סירב לכותרת ושינה אותו לחלקיק האלוהי (the god particle) שכולנו מכירים).

כעת אנחנו יכולים לשאול מהו המודל הסטדנרטי? ממה אנחנו בנויים?
מאז גלמן התגלו עוד שלושה קווארקים (בסה”כ 6), והכוחות החזקים והחלשים בטבע קיבלו עדויות ניסיוניות וניסוחים קוונטיים. בלי להיכנס לעדויות התצפיתיות, זהו המודל השלם (עד כה) של הטבע:

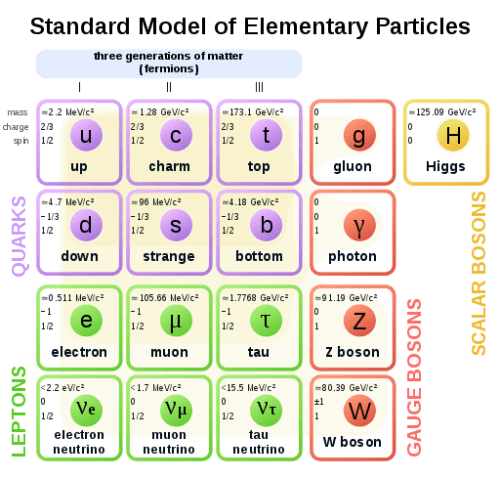
בתמונה מעלה רואים את שלושת הדורות בטבע. אנחנו לא יודעים מדוע ישנם רק שלושה, אבל יש לנו הסבר משכנע מדוע קיימים לפחות שלושה. כל דור הוא שכפול של האחר בתכונותיו מלבד המסה. הקווארקים מעלה ומטה שייכים לדור הראשון, הקווארקים קסום ומוזר בדור השני והקווארקים עליון ותחתון בדור השלישי. מתחתיהם  מופיעים הלפטונים, שניים לכל דור ומחולקים באופן דומה לקווארקים. האלקטרון שאנחנו מכירים שייך לדור הראשון. כל קווארק כזה בעל מטען של “צבע” (שוב אין משמעות לצבע, הפיזיקאים קצת גרועים במתן שמות) ביחס לכח החזק, כשחסרי צבע הם נייטרלים. הלפטונים לעומתם חסרי מטען צבע. בגלל הרגלים היסטוריים שייכנו לפרוטון את המטען החשמלי 1+ , אך משום שהפרוטון אינו חלקיק יסודי, הקווארקים שממנו הוא מורכב  קיבלו מטענים מוזרים של שליש או שתי שליש.
מימינם מופיעים החלקיקים נושאי הכח החלש W,Z (שחלקם גם בעלי מטען חשמלי ובעלי מסה ולכך  השלכות על אינטרקציות אפשריות או על טווח הכח) האחראים להתפרקויות גרעיניות ונושאי הכח החזק – הגלואונים המסומנים באות g , “הדבק” בין הקווארקים שיוצרים את החלקיקים המוכרים לנו כמו הפרוטון או נייטרון (הגלואונים נושאי מטען חזק, או במילים אחרות – צבע, ולכן יכולים לעבור אינטרקציה בין עצמם).

כאן סיימנו את התורה של הכל. טוב, גם זה לא מדויק.

אומנם המודל הסטנדרטי מסביר לא מעט תופעות בטבע, ישנן כמה שאנחנו פשוט לא יודעים להסביר באמצעות המודל. להלן הבעיות המרכזיות:

אוסילציות ניוטרינו – הניוטרינו יכול לשנות את “טעמו” (שוב שם גרוע), או במילים אחרות את דור אליו הוא שייך. אם זה המצב, חייב להיות לו  מסה ולכך עדיין לא מצאנו הסבר משביע רצון (ההיגס לא נותן מסה לניוטרינו).

חומר אפל – נושא לכתבה נרחבת בפני עצמה. בקצרה- זהו רעיון שמנסה להסביר את האנומליה הקיימת בין המסה הנצפית ביקום לבין הכבידה הנמדדת. החומר האפל לא נצפה באופן ישיר, כשזו גם הגדרה עקומה לומר שהחומר לא נראה דרך שום טלסקופ. החומר האפל לא נמצא במודל הסטנדרטי ואין באמת עדויות ניסיוניות במאיצים על קיומו.

והבעייתי מכולם- תורת היחסות הכללית (ועל הדרך גם האנרגיה האפלה): ניסיונות עבר כשלו מל”קוונטט” את תורת היחסות של איינשטיין כדי לקבל תורת כבידה קוונטית. למה? מה שם כשל? כשמקוונטטים שדה שאינו המרחב עצמו המתמטיקה עוד מסתדרת, אבל כשמנסים לקוונטט את המרחב והזמן התאוריה הופכת ללא רנורמזבילית בעליל. פתאום אין שום משמעות לתאוריה וגם אי אפשר לסדר אותה לכזו שתקבל משמעות. עדיין לא פתרנו את הבעיה הקשה הזו אבל הועלו כמה ניסיונות יפים כמו למשל תורת המיתרים שצמחה בכלל מתוך הכוחות הגרעיניים החזקים. בגלל הקושי לחשוף עדויות תצפיתיות ולערוך ניסויים שיחזקו או יפריכו את התאוריה, פיזיקאים נוטשים אותה אט אט אך עדיין שואבים השראה מהרעיונות שלה. אולי אין בכלל מה לנסות בלאחד את התאוריות. אולי הן פשוט לא מסתדרות כי הן לא אמורות להסתדר. אולי הכל בגדר רצון אנושי לא מוסבר למצוא תאוריה שתאחד את הכל ותהיה אלגנטית? טרם קיבלנו תשובה.

מנקודת מבט עכשווית המודל הסטנדרטי נראה ברור מאליו. אבל במבט לאחור, הגילוי נראה כמעט כמו נס. האנשים הנכונים בזמן הנכון העלו במוחם רעיונות גאוניים שנוגדים את האינטואיציה האנושית. בעזרת חוקי סימטריה בלבד הצלחנו להבין ממה אנחנו עשויים ולהסביר במדויק להפליא את הטבע. אם זה לא נס, מהו?

המידע ההיסטורי והמדעי נלקחו מכאן

עוד בנושא באתר הידען:

• מאיץ החלקיקים שיכול להציל את הפיזיקה
• פעמי פיזיקה חדשה?
• רשמי סיור ב-CERN חלק 5: החוקר הישראלי המשתתף בחיפוש אחר פיסיקה חדשה