בחלק השני בוחן אשר יהלום את גבולות הפיזיקה התיאורטית * המאמר פורסם בגליון 7 של כתב העת לענייני תרבות – נכון

הפתרונות האפשריים
למרות האמור לעיל, ברצוני להציע בזהירות הראויה פתרונות פיזיקליים, המתיישבים עם הידע הפיזיקאלי הקיים, לשתי הבעיות: בעיית "המכונית המעופפת"; כלומר, מנוע המאפשר תנועה בשלושה צירים, הלא הוא המנוע היחסותי (מושג שיוסבר בהמשך). וכן, פתרון לבעיית התנועה במהירות העולה על מהירות האור במסגרת תורת היחסות הכללית; פתרון המתבסס על שינוי המטריקה (יוסבר להלן) באזור נתון של המרחב-זמן.
המנוע היחסותי
- תורת היחסות הפרטית
תורת היחסות הפרטית היא תיאוריה של מבנה המרחב-זמן. התאוריה הוצגה בשנת 1905, במאמרו המפורסם של איינשטיין, "על האלקטרודינמיקה של גופים בתנועה". תאוריה זו הייתה תוצאה של תצפיות אמפיריות ושל חוקי האלקטרומגנטיות, אשר גובשו באמצע המאה התשע-עשרה על ידי מקסוול, בארבע המשוואות הדיפרנציאליות המפורסמות שלו, שהובאו לצורתן הנוכחית על ידי אוליבר הביסייד. אחת ההשלכות המרכזיות של משוואות אלה היא כי אות אלקטרומגנטי נע במהירות האור c. תוצאה זו הובילה את החוקרים להאמין כי האור הוא גל אלקטרומגנטי. תובנה זו שימשה מאוחר יותר את אלברט איינשטיין לגבש את תורת היחסות שלו אשר מניחה כי מהירות האור c בריק היא המהירות המותרת המקסימלית בטבע.
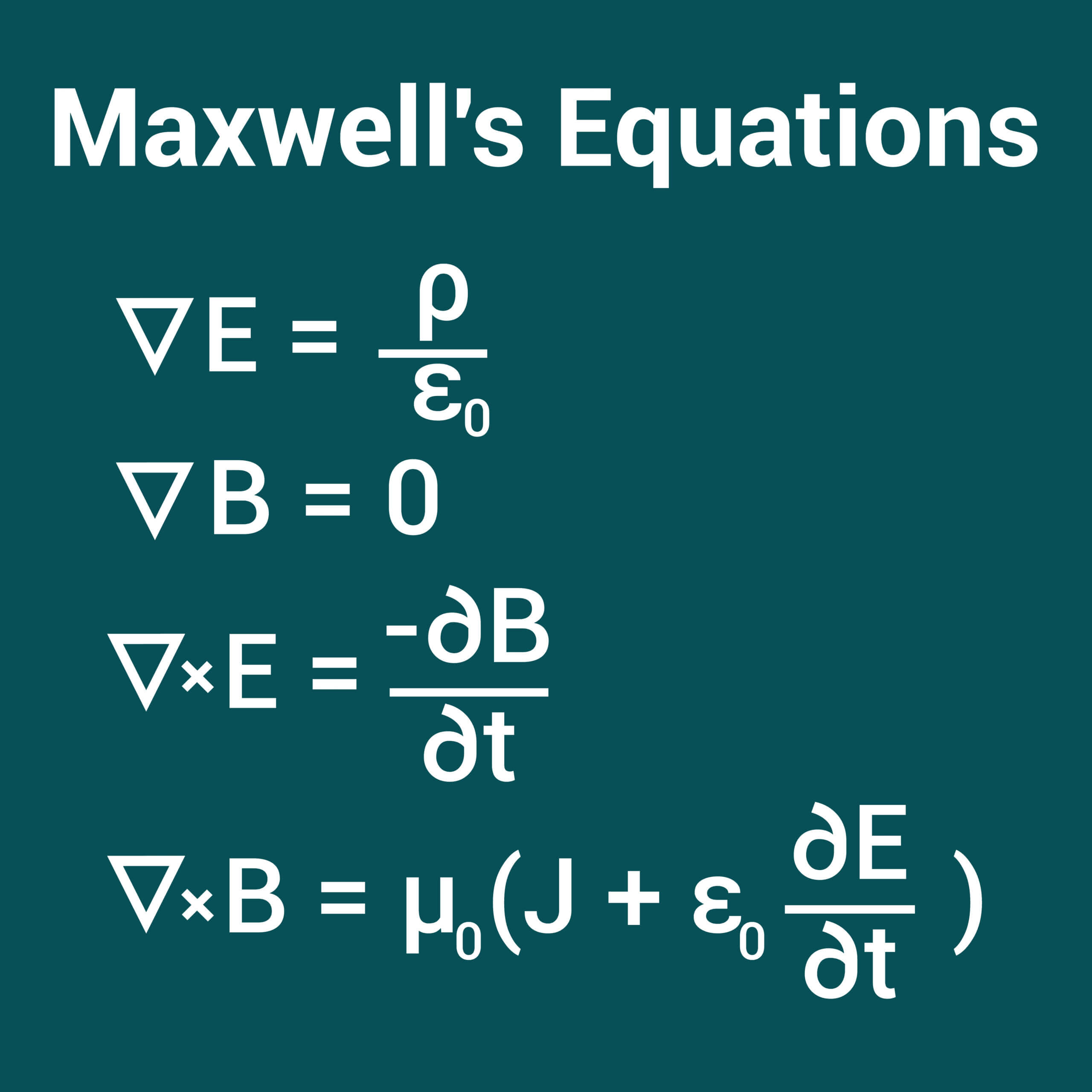
על פי תורת היחסות אין חפץ, מסר, אות (גם אם לא אלקטרומגנטי) או שדה שיכול לנוע מהר יותר ממהירות האור בריק. מכאן נובעת תופעת ה "פיגור" – אם מישהו, שנמצא במרחק R ממני, משנה משהו, אין לי אפשרות לדעת על כך, לפני שיעבור זמן ה "פיגור" שערכו שווה למרחק חלקי מהירות האור.
לשם המחשה, אם נניח שהשמש ברגע זה נעלמה, כמה זמן ייקח לנו לשים לב לכך? את התשובה ניתן לחשב בדרך הבאה: המרחק בין כדור הארץ לשמש הוא: 149.6 מיליון קילומטרים (ראה איור 1), מהירות האור בריק היא: 299,792,458 מטר לשנייה. לפיכך, זמן הפיגור במקרה זה הוא בערך 8.3 דקות.
- חוקי ניוטון
חוקי התנועה של ניוטון הם שלושה חוקים פיזיקליים, אשר יחדיו מניחים את היסודות למכניקה הקלאסית. הם מתארים את מערכת היחסים בין גוף, הכוחות הפועלים עליו, ותנועתו בתגובה לאותם כוחות. שלושת חוקי התנועה נוסחו לראשונה על ידי אייזיק ניוטון בספרו המפורסם, "עקרונות מתמטיים של פילוסופיית הטבע", שפורסם לראשונה בשנת 1687:
החוק הראשון: אובייקט נשאר במנוחה או ממשיך לנוע במהירות קבועה, אלא אם כן מופעל עליו כוח שקול.
החוק השני: במערכת ייחוס אינרציאלית (כלומר לא מואצת), הסכום של הכוחות הפועלים על האובייקט שווה למסתו של אותו האובייקט m מוכפלת בווקטור התאוצה. (בהנחה שהמסה עצמה אינה משתנה).
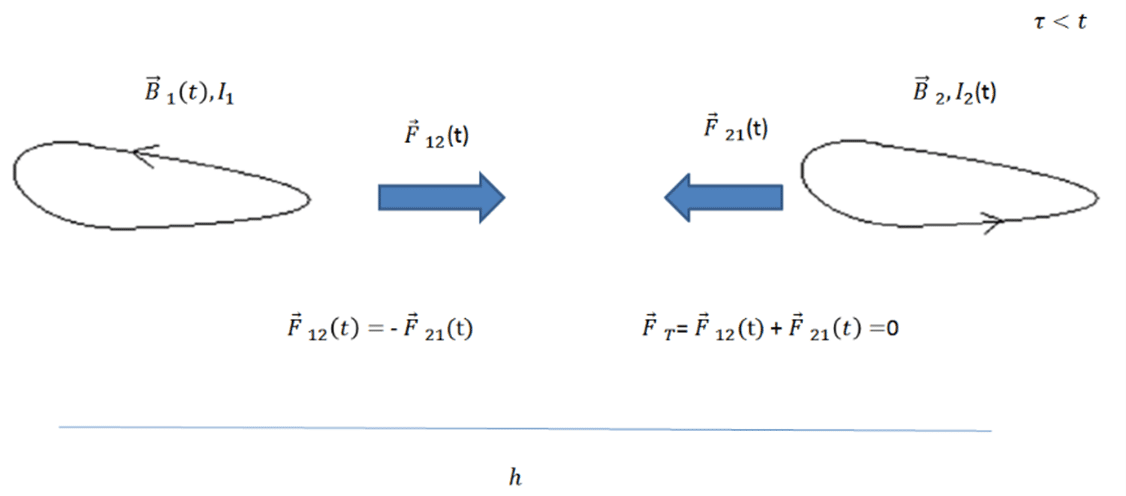
החוק השלישי: כאשר גוף אחד מפעיל כוח על גוף שני, אזי הגוף השני, בו זמנית, מפעיל כוח שווה בגודלו והפוך בכיוונו על הגוף הראשון (ראה איור 2).
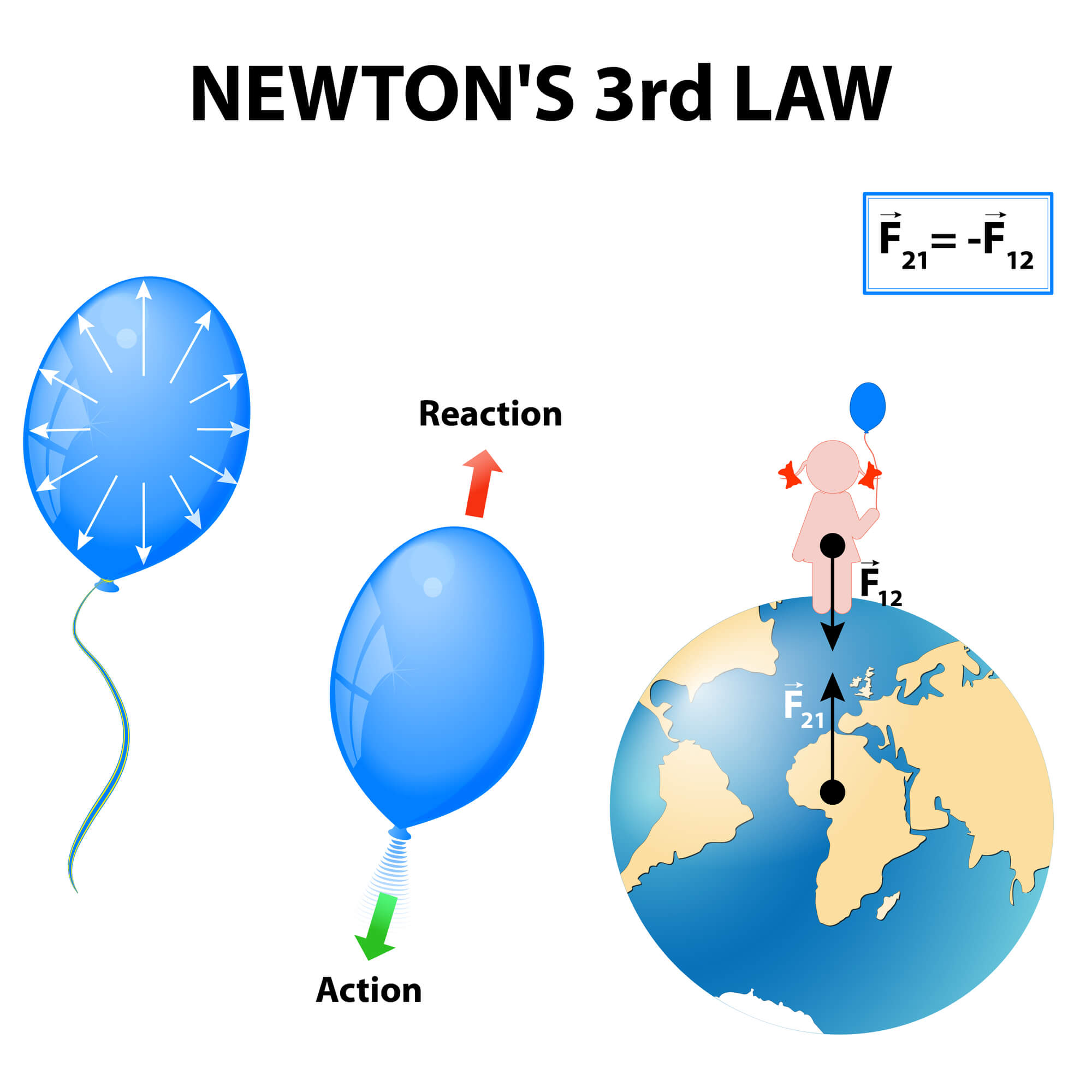
על פי החוק השלישי, הכוח הכולל במערכת שלא מושפעת על ידי כוחות חיצוניים, הוא, אם כן, אפס. לחוק זה יש אימותים ניסיוניים רבים, ונראה שהוא מאבני היסוד של הפיסיקה. עם זאת, לאור הדיון הקודם, ברור כי הפעולה והתגובה לו לא יכול להיווצר בו זמנית, בגלל המהירות הסופית של התפשטות אותות; מכאן, החוק השלישי אינו נכון במובן מדויק, למרות שהוא יכול להיות מספיק מדויק עבור רוב היישומים המעשיים; וזאת, בשל המהירות הגבוהה של התפשטות האותות. לכן, גם הכוח הכולל במערכת לא יכול להתאפס בכל זמן נתון.
- מערכות הנעה
מערכות ההנעה של ימינו מבוססות על יחסים בין שני חלקי מערכת חומרית. כל תנע שמקבל חלק אחד הוא שווה והפוך לתנע שנרכש על ידי החלק השני. דוגמה טיפוסית של סוג זה של המערכת הוא טיל אשר פולט גז כדי להניע את עצמו. התנע של הטיל שווה לתנע של הגז הנפלט בדיוק. רוב המערכות הנעות פועלות על תווך – מכונית נעה קדימה, ובו זמנית מפעילה כוח על הכביש ו"דוחפת" אותו לאחור. גם מטוס דוחף אוויר לאחור. יוצא דופן הוא הטיל, שהודף לאחור את הדלק הרקטי, לכן ניתן לנוע בעזרתו גם בחלל החיצון שם אין מה לדחוף.
מקובל לחשוב, כי בהיעדר גורם חיצוני, סך הכוחות במערכת יהיה אפס, והמערכת לא תשנה את תנועתה. עם זאת, השיקולים היחסותיים לעיל מאפשרים להציע סוג חדש של מנוע. נסתכל במערכת לולאות זרם (איור 3):

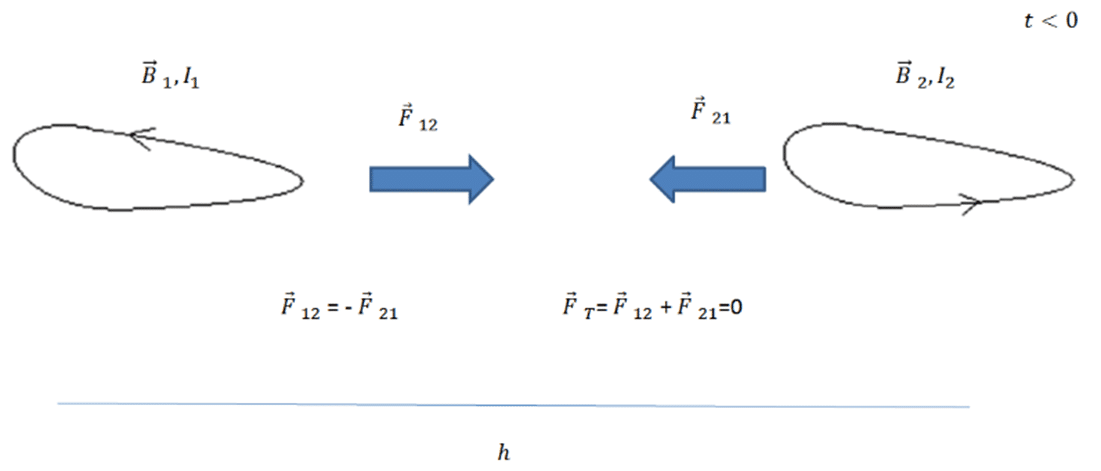
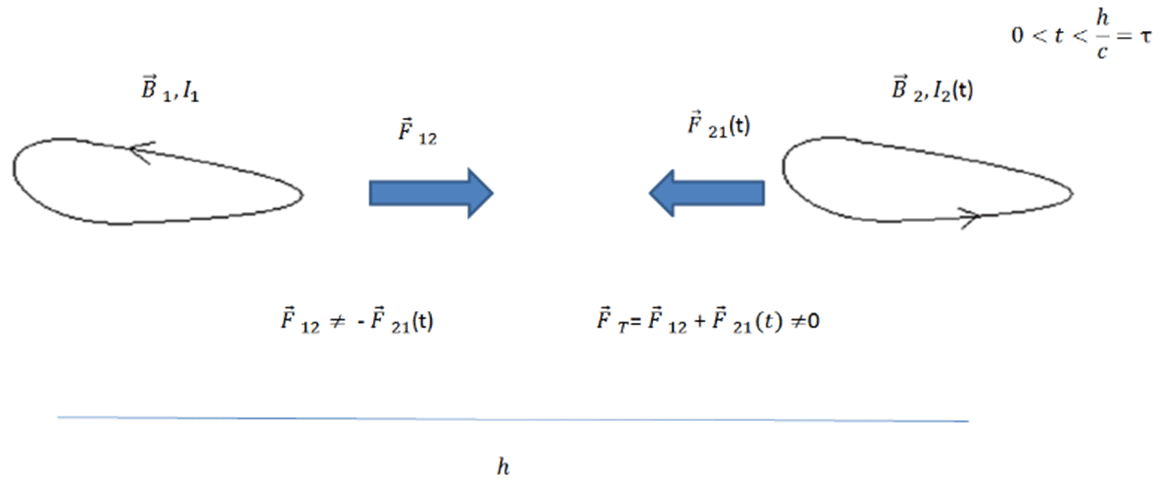
הכוח בלולאת זרם נוצר על ידי שדה מגנטי הקיים בלולאה והזרם הזורם בלולאה. השדה המגנטי הוא תוצאה של הזרם הזורם בלולאה עצמה, אך גם של זרמים בלולאה אחרת. כמו כן, הלולאה המקורית גם היא יוצרת שדה מגנטי בלולאה האחרת, ולכן פועל כוח בין שתי לולאות, כוח שכיוונו נקבע על ידי כיוון הזרם בלולאות. במקרה הסטטי (וה"כמעט" סטטי), הכוח, שמפעילה לולאה אחת על חברתה, שווה בגודלו והפוך בכיוונו לכוח שמפעילה השנייה על הראשונה, בהתאם לחוק השלישי של ניוטון. משמעות הדבר היא ששיקול הכוחות במרכז המסה של המערכת צריך להיות אפס. הדבר שונה, כאשר הזרמים משתנים בזמן, מכיוון ששדה מגנטי, הנוצר על ידי לולאה אחרת, אינו יכול להגיע לולאה המקורית במהירות העולה על מהירות האור, ולכן אין הלולאה מקורית יכולה להרגיש בשינוי באופן מידי. יחד עם זאת, בלולאה האחרת, שינוי הזרם גורם לשינוי כוח מידי. נניח שבזמן t=0 יש שינוי בזרם בלולאה 2 – הכוח בלולאה 2 משתנה באופן מידי, אבל הכוח בלולאה 1 לא ישתנה בזמנים קצרים המקיימים t<T. המשמעות היא שסכום הכוחות הפועל במרכז המסה אינו יכול להיות אפס, שהרי הכוח על לולאה 2 השתנה בעוד הכוח הלולאה 1 נשאר בערכו הקודם. האפקט מודגם באיור 4:
(i)
(ii)
(iii)
חישוב מתמטי מדויק של שקול הכוחות, המבוסס על ההכללה של חוק ביו-סברט לחישוב שדות מגנטיים עבור שדות תלויים בזמן שעשה ג'פמנקו[1], מביא לנוסחה[2] הקושרת בין הכוח במרכז המסה לשינויים בזרמים.
מהנוסחה ברור, שאם קצב השינוי של הזרם לא יהיה גדול מספיק, הכוח הכולל במערכת יהיה זניח. ולכן, יש צורך למתג זרם במהירות גדולה מאד, על מנת לקבל כוח כולל משמעותי.
קיימת גם אפשרות להחליף את אחת הלולאות במגנט קבוע[3]. מנוע יחסותי עם מגנט קבוע מתואר באיור 5:
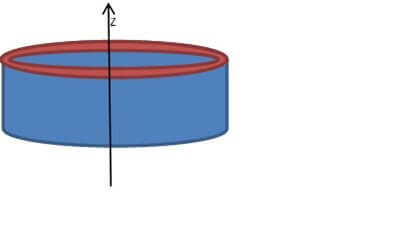
שני חתכים של המערכת מתוארים באיור 6:
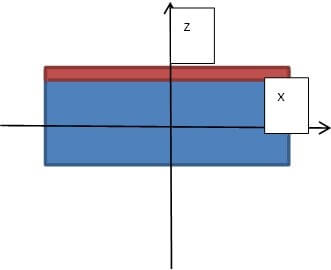

ניתן להראות אם כן שקיים כוח במרכז המסה של המערכות המתוארות לעיל, ועל כן המערכות הללו הן למעשה סוג חדש של מנוע אלקטרומגנטי, מנוע יחסותי. כלומר, זהו מנוע ללא חלקים נעים הפועל על פי עקרונות תורת היחסות.
- שימור התנע
במנוע יחסותי נסתר לכאורה עיקרון שימור התנע. משקיף נאיבי יראה את הגוף החומרי צובר תנע שנוצר יש מאין. לעומת זאת, משקיף מתוחכם יבין שכמות התנע שצובר החומר מתאזנת על ידי התנע שמקבל השדה האלקטרומגנטי[4]. משפט נתר (שנוסח על ידי המתמטיקאית הגרמנייה-יהודייה הדגולה אמה נתר) מכתיב כי כל מערכת בעלת סימטריית העתקה תשמר את התנע.
ואכן, המערכת הפיזיקלית, הכוללת חומר ושדה, סימטרית תחת העתקה, אבל כל תת מערכת (חומר או שדה בנפרד) אינה סימטרית להעתקה. תופעה זו תוארה כבר על ידי פיינמן[5]. פיינמן מתאר שני מטענים הנעים במאונך זה לזה. חישוביו מראים שהחוק השלישי של ניוטון מופר, מאחר והכוחות שמפעיל מטען אחד על השני לא שווים בעוצמתם (והפוכים בכיוונם). פרדוקס זה נפתר על ידי פיינמן בכך שהוא מראה כי התנע, שנרכש על ידי מערכת המטענים, מאוזן על ידי התנע של השדה. הסתירה לכאורה נפתרת, אם כן, על ידי הרחבת החוק השני לחוק שימור התנע המוכלל. חוק זה קובע כי מה שנשמר הוא התנע של המערכת הפיזית, הכוללת גם את החלק של החומר וגם את החלק של השדה. כך, החומר יכול לנוע קדימה, כאשר הוא "דוחף" את השדה האלקטרומגנטי אחור.
- שימור האנרגיה
עיקרון שימור האנרגיה אינו נסתר במנוע היחסותי, הדורש אספקה של אנרגיה להפעלתו. עם זאת, המנוע לא דורש הספקת דלק חומרי להפעלתו, ואפשרי שימוש באנרגיה סולארית (תאים פוטו-וולטאים), במצברים או בחלופות אלקטרומגנטיות (רקטנה – Rectenna). חישובים מראים[6], שעל מנת להפעיל מנוע יחסותי, מהטיפוס שמתואר באיור 6, נדרשת אנרגיה אלקטרומגנטית הגדולה פי שישה מהאנרגיה הקינטית המוקנית למנוע. כלומר, מלבד אנרגיית התנועה נדרשת אנרגיה להניע את הזרמים בתוך המנוע; וזאת, עוד לפני שלוקחים בחשבון הפסדי אנרגיה בגלל התנגדות חשמלית או בגלל חיכוך של כלי הרכב בסביבתו.
- בעיות אינהרנטיות והמנוע היחסותי הטעון
במנוע היחסותי הבלתי טעון, כגון זה המתואר באיור 6, נדרש שינוי קבוע של הזרם על מנת לייצר כוח קבוע. ברור שלא ניתן להגדיל זרם עד לבלי גבול, ובשלב מסוים חייבים להפסיק את גידול הזרם ואז הכוח במנוע מתאפס; יתר על כן, גם שמירה על מהירות קבועה דורשת שינוי קבוע בזרם; כלומר, גם כדי לשמור על המהירות נדרש גידול מתמיד בזרם; מה שאינו אפשרי, ולכן המוצא היחידי הוא עצירה מוחלטת של כלי הרכב. כמובן, ניתן להעלות ולהוריד את הזרם בצורה מחזורית, ולקבל תנועה הדומה לתנועת הבוכנה במנוע בעירה פנימית; אלא שכדי להפוך תנועה כזו לתנועה קווית נדרש להעביר תנע לכביש (כמו שעושה כל מכונית סטנדרטית), ובכך מאבדים למעשה את יכולת התנועה התלת צירית של המנוע; כלומר, את יכולת התעופה. על בעיה זאת ניתן להתגבר בעזרת מנוע יחסותי טעון[7], השונה מהמנוע היחסותי המוצג באיור 6, בכך שהוא מכיל מטען חשמלי (ראה למשל באיור 7).
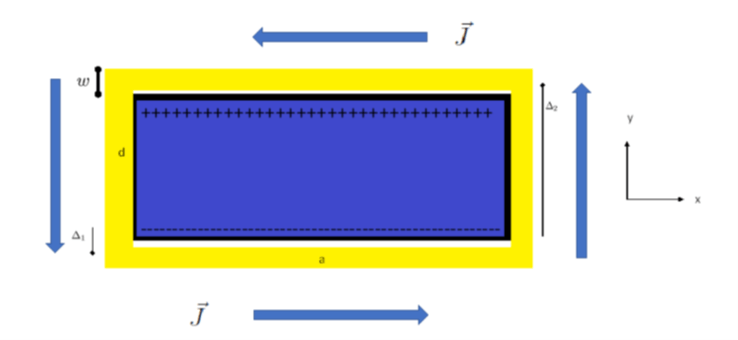
איור 7: דוגמא למנוע יחסותי טעון המטענים החיוביים מתוארים על ידי הסימן + והשליליים על ידי הסימן -.
מנוע כזה מסוגל לשמור על מהירות קבועה גם כשהזרם קבוע. החיסרון הבולט שלו הוא בכמות המטען החשמלי הנדרש, שמשמעותו צפיפות מטען גדולה בכל נפח סביר, ולכן, גם פריצה חשמלית מסוכנת. מנוע מסוג זה, שמייצר תנע סביר ואינו גורם לפריצה חשמלית, צריך להיות גדול מאד, ולכן גם המהירות שתתקבל תהיה נמוכה; מאחר שהנפח גדול פירושו גם משקל גדול, וכידוע, המהירות שווה לחלוקה של התנע במשקל.
- סיכום
המסקנה היא כי ניתן לבנות מנוע המבוסס על עקרונות תורת היחסות ועל חוקי האלקטרומגנטיות. למנוע זה התכונות הבאות:
- מאפשר תנועה של 3 צירים (כולל אנכי), ולכן מתאים למכונית מעופפת.
- ללא חלקים נעים
- צריכת הדלק אפסית
- אפס פליטת פחמן
- זקוק לאנרגיה אלקטרומגנטית בלבד (שאפשר לספק על ידי פאנלים סולאריים)
- מהווה פתרון אידיאלי לנסיעות בחלל, מכיוון שהיום חלק ניכר ממסת כלי החלל מוקדש לדלק
- יעיל מאד. עקרונית, ניתן להמיר חזרה את האנרגיה הקינטית של המנוע לאנרגיה אלקטרומגנטית ולאחסן אותה במצבר (כפי שנעשה היום באופן חלקי ברכבים היברידיים)
בעת הנוכחית, המנוע עדיין חלש לשימוש מעשי, אך ישנם כיווני מחקר לשפרו. בין השאר, נשקל לעשות שימוש בצפיפויות המטען הגבוהות מאד הקיימות ברמה האטומית[8].
תנועה במהירות העולה על מהירות האור

הדעה המקובלת היא שתנועה במהירות העולה על מהירות האור עומדת בסתירה לעקרונות תורת היחסות, ולכן, במידה ותורת היחסות נכונה, תנועה כזאת היא בלתי אפשרית. לכן, גם מסע בין כוכבים, כפי שמתואר בסרטי העתיד הרחוק בקולנוע ("מסע בין כוכבים", "מלחמת הכוכבים", "חולית" וכו') אינו אלא דמיון בלבד.
הסיבה לכך היא, שמתוך משוואות התנועה של תורה היחסות הפרטית ניתן לראות שהאצה של חלקיק בעל מסה סופית למהירות הקרובה למהירות האור דורשת אנרגיה גבוהה מאד, ואילו האצה של חלקיק כזה למהירות האור דורשת אנרגיה אינסופית. מכיוון שאין לנו אנרגיה אינסופית, לא ניתן להאיץ חלקיק למהירות האור, ובוודאי שלא למהירות שעולה עליה.
נציין שהפוטון (חלקיק האור) הוא חסר מסה, ולכן נע במהירות האור. כמו כן, ניתן להאיץ חלקיקים קלים, כגון האלקטרון, למהירות הקרובה מאד למהירות האור (98% ממהירות האור), במאיצים צנועים, כגון זה המצוי באוניברסיטת אריאל.
שאלה מעניינת נוספת קשורה בחלקיקים שמלכתחילה נמצאים במהירות הגבוהה ממהירות האור. מעיון במשוואות התנועה, נגלה שבמקרה כזה תידרש אנרגיה אינסופית, כדי להוריד את מהירותם אל מתחת למהירות האור. כלומר, תנועה מעל למהירות האור אפשרית, אך בלתי אפשרי הוא המעבר בין התחומים; כלומר, בלתי אפשרי להפוך חלקיק הנע במהירות הגבוהה ממהירות האור לחלקיק הנע במהירות הנמוכה ממהירות האור, ולהפך.
עיון במשוואות התנועה מגלה שהסיבה נעוצה במבנה של המרחב זמן הבא לידי ביטוי בגודל מתמטי המכונה "מטריקה". לקורא, חסר הרקע המדעי, נסביר שגודל זה הוא למעשה הסיבה לשונות של הזמן מהמרחב בטבע. המטריקה המקובלת בתורת היחסות הפרטית היא המטריקה שקרויה על שם המדען ההולנדי המפורסם לורנץ. בספרות המדעית, נהוג להתייחס למבנה הנתון של המרחב זמן כאקסיומה; כלומר, הנחת יסוד שאינה נגזרת מתוך הנחות קודמות.
במאמר שהתפרסם בשנת 2008[9], התברר שניתן לחזק את תורת היחסות הפרטית (במובן של הפחתה במספר ההנחות הנדרשות לצורך פיתוח התיאוריה) על ידי כך שאין מניחים מראש מטריקה של לורנץ, אלא מאפשרים מטריקה כללית, ובודקים את היציבות של המטריקות השונות תחת המשוואות של תורת היחסות הכללית (משוואות איינשטיין). מתברר, שמכל המטריקות האפשריות, רק המטריקה של לורנץ יציבה בתנאי ריק או צפיפות חומר נמוכה. ניתוח זה מסביר למה בפועל המרחב והזמן שונים, והמטריקה המתאימה לתיאור המרחב-זמן היא המטריקה של לורנץ; אך, מאידך גיסא, אין צורך להניח מטריקה זו באופן דוגמטי.
למעשה קיימת אינדיקציה שבזמן המפץ הגדול, בעת שצפיפות החומר הייתה גבוהה, התקיימה תנועה במהירויות העולות על מהירות האור; מה שהביא לשיווי משקל תרמודינמי, כפי שניכר מהתפלגות סוגי החומר בטבע (בעיקר הליום ומימן), ומהאחידות הבלתי רגילה של קרינת הרקע הקוסמית. כלומר, בהתחלה המטריקה לא הייתה לורנציאנית, אלא ככל הנראה דווקא אוקלידית (קרויה על שמו של הגיאומטריקן היווני הקדום אוקלידס) – מטריקה זו אינה מבחינה בין המרחב והזמן, ומאפשרת תנועה במהירות העולה על מהירות האור.
ברמה התיאורטית, השאלה האם קיימת התפלגות חומר התומכת במטריקה אוקלידית יציבה היא שאלה פתוחה, אבל נניח לרגע שהתשובה לשאלה הזו חיובית.
אם התשובה חיובית, ניתן לתאר חללית הפועלת באופן הבא: ראשית, היא מאיצה עד למהירות הקרובה למהירות האור. אז, בעזרת מנוע נוסף, היא משנה את התפלגות החומר, כך שתיווצר סביבה מטריקה אוקלידית, בה היא יכולה לעבור ממהירות הנמוכה ממהירות האור למהירות הגבוהה ממהירות האור ללא קושי. בשלב זה, ניתן לכבות את המנוע המשמש לשינוי המטריקה, ולהמשיך במהירות, העולה על מהירות האור במרחב-זמן רגיל, ואף להאיץ. נזכיר שהקושי העקרוני הוא רק לעבור את מהירות האור, במרחב שנשלט על ידי מטריקה לורנציאנית, אך אין שום קושי עקרוני להאיץ, לאחר שעברנו מהירות זו. תיאור טכני יותר של סיטואציה זו מתואר בספרות המדעית[10].
כמובן, עולות שאלות רבות לגבי מקרה זה: למשל, מה יקרה למבנה חומר כאשר המרחב-זמן יהפוך להיות אוקלידי, והאם יצורים ביולוגים יכולים לשרוד מעבר שכזה? שאלות אלו נוספות לשאלות הבסיסיות יותר – האם, מבחינה טכנולוגית, ניתן לייצור טרנספורמציה אוקלידית שתאפשר לחלליות לנוע במהירות העולה על מהירות האור ולבני אדם להגיע לכוכבים?
ימים יגידו.
[1] Jefimenko, O. D., Electricity and Magnetism, Appleton-Century Crofts, New York (1966); 2nd edition, Electret Scientific, Star City, WV (1989).
[2] Miron Tuval & Asher Yahalom "Newton’s Third Law in the Framework of Special Relativity" Eur. Phys. J. Plus (11 Nov 2014) 129: 240 DOI: 10.1140/epjp/i2014-14240-x. (arXiv:1302.2537 [physics.gen-ph]).
[3] Asher Yahalom “Retardation in Special Relativity and the Design of a Relativistic Motor”. Acta Physica Polonica A, Vol. 131 (2017) No. 5, 1285-1288. DOI: 10.12693/APhysPolA.131.1285.
[4] Miron Tuval & Asher Yahalom "Momentum conservation in a relativistic engine” Eur. Phys. J. Plus (2016) 131: 374. DOI: 10.1140/epjp/i2016-16374-1.
[5] R. P. Feynman, R. B. Leighton & M. L. Sands, Feynman Lectures on Physics, Basic Books; revised 50th anniversary edition (2011).
[6] Shailendra Rajput, Asher Yahalom & Hong Qin "Lorentz Symmetry Group, Retardation and Energy Transformations in a Relativistic Engine" Symmetry 2021, 13, 420.
[7] Rajput, Shailendra, and Asher Yahalom. 2021. "Newton’s Third Law in the Framework of Special Relativity for Charged Bodies" Symmetry 13, no. 7: 1250. https://doi.org/10.3390/sym13071250
[8] A. Yahalom "A Nano Relativistic Motor" in preparation.
[9] Asher Yahalom "The Geometrical Meaning of Time" [“The Linear Stability of Lorentzian Space-Time” Los-Alamos Archives – gr-qc/0602034, gr-qc/0611124] Foundations of Physics http://dx.doi.org/10.1007/s10701-008-9215-3 Volume 38, Number 6, Pages 489-497 (June 2008).
[10] Asher Yahalom "Gravity and Faster than Light Particles" Journal of Modern Physics (JMP), Vol. 4 No. 10 PP. 1412-1416. DOI: 10.4236/jmp.2013.410169. Pub. Date: October 31, 2013
המחבר: אשר יהלום, המחלקה להנדסת חשמל ואלקטרוניקה, הפקולטה להנדסה, אוניברסיטת אריאל בשומרון * המאמר פורסם בגליון 7 של כתב העת לענייני תרבות – נכון
לחלק הראשון של המאמר (מתפרסם במקביל)
עוד בנושא באתר הידען:

15 תגובות
מולה , וזה מה שבני האדם יהפכו, למידע דיגיטלי ,אם קצב ההתקדמות ימשך
לגל , אתה יכול גם לשלוח לייזר מכדור הארץ לירח ולהזיז אותו על שטח הירח בקו ישר כביכול מהר יותר ממהירות האור אבל זה רק אשליה אופטית
בני אדם יוכלו לנוע במהירות האור ובזול רק כשהם יהפכו לדיגיטליים וינועו בחלל כמידע בעזרת לייזר. אז גם קונספט הזמן לא חשוב ו 100,000 או 4 שנות אור לא ישנו הרבה לאדם דיגיטלי
התגלו חלקיקים מהירים יותר ממהירות האור?
המדענים לא מבינים דבר אחד פשוט , אם אתה רוצה לטוס במהירות האור ,,, אתה צריך להיות אור , אין אפשרות אחרת.
יש לי תאוריה, רכיבה על גלי כבידה.
ככל שמקור גל הכבידה רחוק יותר כך מהירות הרכיבה על גביו גבוהה יותר ואף יכולה לעבור את מהירות האור.
הרעיון הוא להבין כיצד לשייך עצם לגל כבידה אחד על חשבון אחר.
סליחה על בעיות העריכה בהערות הקודמות שלי (כנראה המעבר דרך Notepad לא היטיב איתן
לגל: שום הפרעה מכנית במוט אינה מתקדמת מהר יותר ממהירות הקול בו, וזאת נמוכה בהרבה ממהירות האור. כלומר, עד שהאיש במאדים יבחין בתזוזה החבר הטלפוני שלו יוכל לספר לו מה הוא עומד לראות בעוד די הרבה זמן…
לגל, האנרגיה שאתה מעביר למוט תעבור בו במהירות הקול במוצק, שהיא נמוכה בהרבה ממהירות האור. אם הצלחת לדחוף אותו 5 ס"מ בתוך עשירית שניה, הרי שהקצה שקרוב אליך מספיק אלסטי כדי לאפשר את זה, וגל הדחיסה ימשיך לכיוון מאדים והשרידים הלא מובחנים שלו (כי יש ספיגת אנרגיה במוט) יגיעו למאדים בתוך כמה חודשים, או שהמוט פשוט קרס איפשהו קרוב אליך, ואז שום דבר לא יגיע למאדים.
גל,
המוט מןרכב מאטומים ברגע שאתה מזיז את האטום הקיצןני השדה החשמלי שמושך את השכן יעביר פולס לשכן במהירות האור שיבוא יחד איתו וכן הלאה (כפול מספר האטומים) מהירות האטום אגב קטנה ממהירות האור . חישוב משיכת האטום בשדה חשמלי היא שאלה קוונטית. בקיצור האות יגיע לאט ממהירות האור.
מאחר והוכח מעל לכל ספק שקיימים עבים שמבקרים בדור הארץ זה זמן רב וכאחד שצפה בחללית כזו אין לי ספק שיש הגיון בדברים ושעולם האלקטרו מגנט ילך ויתפתח אולי לא במאה שלנו אבל המאה הבאה ודאי
תודה רבה, אחלה כתבה!
תודה
שאלה לקוראים, ולמתעניינים,
נניח מוט קשיח וישר בין מאדים לכדור הארץ.
נניח לצורך הניסויי מאדים וכדור הארץ לא בתנועה.
קצה המוט A שבצד כדה"א מונח על השולחן , הקצה השני B במאדים מונח שם על שולחן.
מזיזים את קצה המוט על כדה"א נינח 5סמ לכיוון מאדים.
האיש במאדים מזיז בחזרה את המוט.
שאלות
1.הזזת המוט נעשתה בזמן נניח 0.1 שניה, הרבה יותר מהר ממהירות האור הלוך/וחזור ממאדים לכדה”א, האם זה אפשרי?
2. אם כן, אז אפשר להעביר מידע הרבה יותר מהר ממהירות האור?
3. אשמח לקבל תשובות בנושא.
אשר יהלום לפחות חושב על העתיד. יש כאלה שהכל ברור להם ורק נותר לאכול סנדוויץ'.