המשוואה המפורסמת ביותר בקוונטים פורסמה בשנת 1926 על שני עמודים בלבד. מה היא מתארת וכיצד שרדינגר חשב עליה?
המדען האוסטרי ארווין שרדינגר היה קוסם מדעי. ארנולנד זומרפלד, מחלוצי תורת הקוונטים התייחס בעבר למשוואה שהפכה את שרדינגר למפורסם "כתגלית המופלאה ביותר מבין כל התגליות המופלאות של המאה העשרים". כשמקס פלאנק, מהראשונים לזהות את אופיו הקוונטי של האור, החזיק בידו את המאמר השני של שרדינגר הוא צוטט בלהט אומר: "אני קורא את מילותיך כילד סקרן ונלהב המנסה לפענח חידות שהטרידו אותי זמן רב ואני נמוג מהיופי שעיניי מגלות. אני חייב להעמיק ברעיונותיך כדי לתפוס אותן במלואן".
שנים לאחר מכן ריצ'רד פיינמן, שזכה בפרס נובל על ניסוח התורה האלקטרומגנטית הקוונטית, אמר על שרדינגר: "מהיכן הוא הביא אותה (את משוואת שרדינגר)? משום מקום. לא ניתן לחלץ אותה משום מקום. היא הגיעה ממוחו של שרדינגר, בזמן שניסה להבין את התצפיות הניסיוניות של העולם האמיתי". בדומה לפיינמן, היסטוריונים סבורים ששרדינגר מעולם לא הסביר כיצד המשוואה המפורסמת ביותר בקוונטים צצה במוחו אבל אין ספק שניתן לנחש אילו רעיונות הובילו לניסוח המאמר המהפכני בשנת 1926.
שרדינגר שאב השראה מפרויקט הדוקטורט של חוקר צעיר בשם לואי דה ברוי. בעקבות האפקט הפוטואלקטרי שתואר על ידי אלברט איינשטיין, דה ברוי הניח שגם לחלקיקי החומר תכונות גליות. התזה השנויה במחלוקת נשלחה לשרדינגר שבהתחלה אפילו לא טרח להתייחס אליה. להפתעתו של דה ברוי, היה זה אלברט איינשטיין שהתלהב מהמאמר והצית את הרעיון בקרב הקהילה המדעית. כמה חודשים לאחר מכן הפיזיקאי פיטר דבאי ביקש משרדינגר להעביר הרצאה על התזה של דה ברוי בציריך. כשההרצאה נגמרה פנה דבאי לשרדינגר ואמר: "אם מה שאתה אומר נכון, כלומר שחלקיקים אכן מתנהגים כגלים, בטח קיימת משוואת גלים שמתארת אותן, למה שלא תנסה למצוא אותה?" ואכן כך היה.
שרדינגר שנהג לנסוע לחופשות בלי אשתו (ואף קיים רומנים עם נשים נוספות), החליט גם הפעם לנסוע הרחק לבדו בכדי לפצח את הבעיה. בסיום החופשה הוא החזיק במאמר הכתוב בדף אחד משני הצדדים המפרט את משוואת הגלים הידועה כיום בתור משוואת שרדינגר. כדי להסביר את המאמר הקצרצר נדרש ידע מוקדם על מכניקה אנליטית ולמען האמת יש שיטענו ששרדינגר לא באמת פיתח את המשוואה מעקרונות יסוד, אלא הניח שהיא נכונה. אז מהי משוואת שרדינגר? דואליות הגל חלקיק של דה ברוי יחד עם העובדה שגלי אור מישוריים מתקדמים בזמן פרופורציונלית לאנרגיה הובילה את שרדינגר לרשום את המשוואה הבאה:
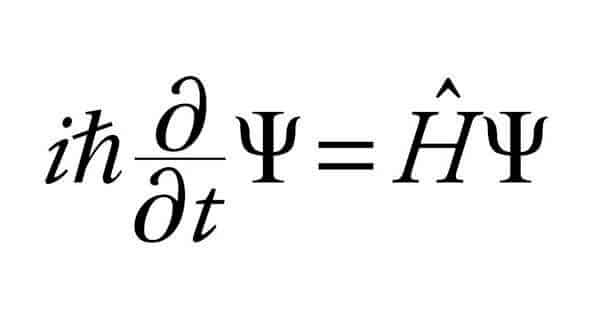
המשוואה מורכבת משני חלקים: צד ימין מכפיל את האנרגיה של החלקיק (השקולה לביטוי H, ההמילטוניאן) עם פונקציית הגל שלו (המסומן באות היוונית פסיי) וצד שמאל משערך את הנגזרת בזמן של פונקציית הגל. במילים אחרות, השינוי בזמן של פונקציית הגל שקולה לאנרגיה של החלקיק. לפני שנמשיך אני רק רוצה להדגיש עד כמה המשוואה הזו אלגנטית. האנרגיה של החלקיק היא זו שמאלצת את פונקציית הגל להשתנות בזמן. אם נחליף את H בערך מספרי כלשהו, הפתרון למשוואה זו תזכיר פונקציה של גל מישורי. במכניקת הקוונטים H הוא לא מספר, הוא אופרטור. אופרטור כשמו כן הוא, מבצע פעולה על האובייקט עליו הוא פועל. במקרה שלנו, H פועל על פונקציית הגל פסיי. אם פסיי מתאר מצב פיזיקאלי של חלקיק עם אנרגיה מוגדרת, H יתחלף באנרגיה השייכת לפסיי. אם פונקציית הגל מתארת סופרפוזיציה של מצבי אנרגיה (כלומר החלקיק יכול להיות בכמה מצבי אנרגיה שונים, כל אחד בהסתברות מסוימת), מתמטית פסיי ייכתב כסכום של מצבי אנרגיה מוגדרים. במקרה הזה H יפעל על כל אחד ממצבי האנרגיה בנפרד ויוחלף בערכו כפקטור המצומד לכל מצב בהתאם. ההפעלה של H על המצב פסיי מכתיבה בכל רגע כיצד הוא משתנה.
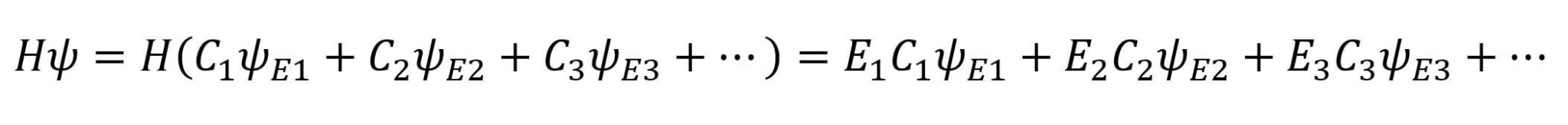
לעיתים משוואת שרדינגר נראית כך:
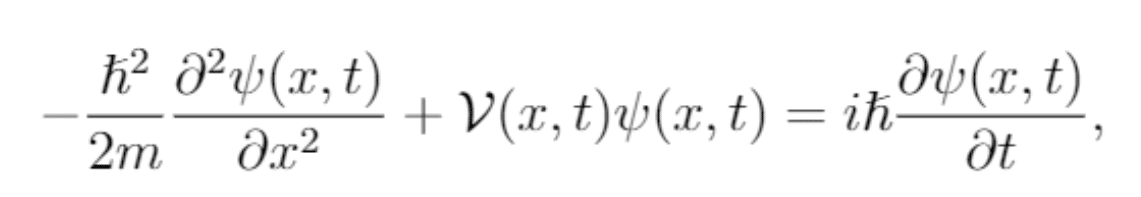
המשוואה הזו היא בסה"כ כתיבה שונה של אופרטור האנרגיה H בעזרת רכיביו – לכל חלקיק יש אנרגיה קינטית ואנרגיה פוטנציאלית (המסומנת באות V). משיקולים לדומים שהובילו פיזיקאים להקביל בין גלים מישוריים אלקטרומגנטיים לפונקציות גל חלקיקיות, ניתן להחליף את האיבר הקינטי בנגזרת שנייה של המרחב. כשכותבים את ההמילטוניאן כך, משוואת הגלים נחשפת במלואה. כאן חייבים לעצור לרגע ולהעיר הערה טכנית – משוואת גלים אמיתית מכילה נגזרת שניה גם במרחב וגם בזמן, בשונה ממשוואת שרדינגר המערבת נגזרת ראשונה בזמן ונגזרת שניה במרחב. יחד עם זאת, השימוש במונח פונקציית הגל לתיאור הפתרון למשוואת שרדינגר אינו שגוי מתמטית כי הפיתרון אכן נראה כמו גל מרחבי (זאת בזכות האיבר המדומה i).
תפקידה של משוואת שרדינגר היא לחשב את פונקציית הגל פסיי בכל רגע. ערך המוחלט פונקציית הגל בריבוע מתאר את ההסתברות של החלקיק להימצא במיקום מסוים בזמן כלשהו. משוואת שרדינגר הוכחה כיעילה בחיזוי התנהגותם של חלקיקים בטבע וקבלה משנה תוקף כאשר הצליחה לתאר במדויק את מבנה אטום המימן. על אף ההצלחות הרבות של משוואת שרדינגר קיימות בה לא מעט מגבלות. המשוואה איננה משוואה יחסותית (המשוואה מתייחסת שונה לזמן ולמרחב, והאנרגיה H המתוארת במשוואה האחרונה אינה יחסותית) בנוסף היא איננה מסוגלת לתאר יותר מחלקיק יחיד. שנים לאחר מכן, קליין, גורדון ודיראק ניסחו משוואות יחסותיות דומות למשוואת שרדינגר ותורת השדות פתרה את התעלומה של תיאור מערכות רב חלקיקיות. משוואת שרדינגר נחשבת לאבן יסוד במכניקת הקוונטים ונעשה בה שימוש עד היום. לשרדינגר תרומות רבות במדע אבל אין ספק שהאינטואיציה החדה של הפיזיקאי הגאון הופיעה בגדולתה במשוואה אחת ששינתה את תפיסתינו על העולם ועל חוקי הטבע.
בכל שבוע אקדיש כתבה לרעיון או למושג שגור בפיזיקה מודרנית. אם יש לכם הצעות או בקשות לפינה זו אתם מוזמנים לפנות אליי בכתובת המייל: [email protected]

9 תגובות
כמה שטויות במקום אחד
המשוואה שרידנגר לוקה בחסר מאחר והוא כתב אותה לא לפי גילוי מחקרי אלה ברמאות והמשוואה הזאות היתה ידועה לי לפניו.ובכתבה מצינים שאין הסבר איך הגה אותה.ומאחר והני הגיתי אותה לפניו אז להוכיח זאת הספר את הצורה בה הוא כביכול הגה.א.כול הוא לא הגה מה שהוא עשה זה שהיו עוד מדענים שחיפשו את המשואה ועלו המון אפשרויות מה שעשה הוא שהוא אסף את כול האפשרויות שהגיעו המדענים ובעזרתם כול האופציות שהתבררו כלא נכונות .התבררה אופציה אחת שלו עלתה בראשם מאחר והם טעו בחישובים והגיעו למבוי סתום שבוא אין עוד אופציות .ונשארה אופציה ממש פשוטה שלא נוסתה מהנראות שהיא לא הגיונית ולא קבילה ובקיצור המדענים הגדולים חיפשו בשמים והיא היתה מול עינהם וחסרת משמעות ושדינגר שידע שאין אפשרות שיכולה להיות מקובלת ואז הציע את המשווא ושם את שמו וכבודו שהיא נכונה רק מהסיבה שלא ניתן להוכיח שהיא לא נכונה וגילוי אי נכונותה הוא שווה ערך לפיתרון ומאחר והבין זאת הימר בבטחון שזוהי המשואה הנכונה .אך ברור שהושגה במרמה ולו בהגיה אלה בניסוי וטעיה שניסו מדענים ענקים ששללו משוואות שלא תאמו וכאמור הוא לא התאמץ בכלל וזו ממש רמאות .ואני חשבתי על כך שהציע את המשוואה שהשללילה שלה היא כמו לפתור חידה לא ניתנת לפתירה ואים תוכל להכחיש את הפתרון אזי פתרתה את החידה .אני מקווה שבעקבות דברי אלו ישלל ממנו הקרדית ויעונק למדענים שהם פתרו בהמצעות האפשרויות שהם שללו ומיצו את כול האפשרויות ועל זה מגיע להם הפרס.צריך להבין שעוסקים בנושאים כאלה ההשקעה המחשבתית מביאה אותך למיצוי מחשבה עצומה שבה אתה בודק אפשרויות שהם בגובה רב וקשה להאמין בקלות הפתרון.ולכן יש שדוחים את המשוואה שמבחינתם המשוואה הזאות נשללה בתחילה כחסרת יכולת וכלו נכונה
החתול נימצא בחלק השני
הוא יוצר את האפקט ואז נעלם
זאת אחת הכתבות הטובות שלך!
איזה יופי שהכנסת גם את המשוואה המתמטית ולא רק את הסברת את הרעיון במילים.
Erwin with his psi can do
Calculations quite a few.
But one thing has not been seen:
Just what does psi really mean?
מדע חייב להיות מובן ומוסבר היטב.
לא הבנתי כלום מההסבר שלך. חבל. למען השקיפות אני דוקטורנטית לביולוגיה
הסבר מעולה, מדהים בפשטותו, כל הכבוד
מה עם החתול של שרדינגר? איך זה קשור?
שרדינגר קיבל את המשוואה מנוסע בזמן שמצא אותה כתובה בספר לימוד על מכניקת הקוואנטים ומשוואות שרדינגר. רק ככה אפשר להתקדם לפעמים בפיזיקה