בעיית המדידה

האם פונקציית הגל מתארת את המציאות או רק את הידע שלנו עליה? שלוש בעיות יסוד — התוצאה, הסטטיסטיקה והאפקט — מגלות שסוגיית המדידה אינה רק שאלה פילוסופית

על בעיית המדידה נכתבו אינספור מאמרים. לכסות את כולם בפוסט אחד זו משימה בלתי אפשרית. אני לא אתיימר לפרט כאן הכל, אבל חשבתי לכתוב עליה במטרה להסביר מדוע חלקנו מאמינים שזו אכן בעיה אמיתית ומדוע חלקנו חושבים שזו רק אשליה. את הבלבול המחיש זוכה פרס הנובל לפיזיקה, ריצ׳רד פיינמן: ״תמיד היה לנו (זה סוד, סוד, סגרו את הדלת!), תמיד היה לנו הקושי בלהסביר את העולם דרך מכניקת הקוונטים. לפחות אני כזה. לא הצלחתי להשלים עם העובדה שנושא זה ברור לי. טוב, אני עדיין מרגיש בלחץ מזה…., אתם יודעים איך זה, בכל תחום חדש, לוקח דור או שניים כדי להבין שאין באמת בעיה. עדיין לא ברור לי שאין כאן באמת בעיה. אני לא יכול להגדיר את הבעיה, לכן אני חושד שאין כאן באמת בעיה, אבל אני לא יכול לדעת שאין כאן בעיה באמת״.

הציטוט מאיר את התחושה הכללית בקרב הקהילה המדעית. מצד אחד, הפילוסופים טוענים בבירור שקיימת בעיה עם איך שמדידה מוגדרת במכניקת הקוונטים, מצד שני, כשיורדים לעומקה לא ברור מה שורש הבעיה.

בכתבה זו אתמקד בגישתו של טים מאולדין (פילוסוף למדע) שסיכם בשלושה פרקים את בעיית המדידה, אך לפני שאפרט את הבעיות, אתחיל בפרשנות קופנהגן למכניקת הקוונטים שנלמדת בקורסי היסוד באוניברסיטאות ברחבי העולם. פרשנות זו מניחה שלכל מערכת פיזיקלית — מחלקיק בודד ועד השמש, מאדם יחיד ועד היקום כולו — משויך וקטור מצב, או כפי שהיא מכונה בידי רבים, פונקציית גל.  פונקציה זו נושאת את כל המידע הדרוש לתיאור מצבה הפיזיקלי של המערכת. בניגוד לפיזיקה הקלאסית, שבה מצב נקבע באמצעות גדלים דטרמיניסטיים כמו מיקום ותנע מוגדרים היטב, חלקיק יכול להיות במצב מעורב – ״קצת כאן וקצת שם״. המצב הקוונטי החדש מערבב כמה מצבים קלאסיים ביחד. יחד עם זאת, ביום יום איננו רואים חלקיק ״קצת בכל מקום״. המשפט הזה דיי סתמי, הרי מיקומו של חלקיק לא יכול להיות כפול בו זמנית. אם כך מה המשמעות של פונקציית הגל? ערבוב המצבים הקלאסיים מתייחס להסתברות של צופה למדוד, כלומר לראות בצורה כזו או אחרת את החלקיק באחד מהמיקומים. לאחר המדידה, לרגע, מיקומו של החלקיק מוגדר היטב. לאחר המדידה, אין כבר באמת הסתברות שחלקיק ימצא בכמה מקומות, הרי ברור שלאחר המדידה, מיקומו של החלקיק הוא יחיד. לכן, כל ההסתברויות קורסות לאפס מלבד לזו ששייכת למיקומו האמיתי של החלקיק שהופכת ל-100%.

כאן נעוצה בעיית המדידה – שרדינגר הראה שפונקציית הגל משתנה בזמן לפי משוואה פשוטה יחסית, לינארית במהותה, ושום משוואה לינארית יכולה לגרום לקריסה כה דרמטית. אז מהי הדינאמיקה האמיתית של מכניקת הקוונטים? אם כולנו הרי אובייקטים שעשויים מחלקיקים, והדינאמיקה היחידה היא לינארית, קריסה לא יכולה להתרחש.

בעייה ראשונה – בעיית התוצאה

בניסוח מתומצת יותר, שלושת הטיעונים הבאים לא יכולים להתקיים בו זמנית

1. פונקציית הגל מתארת את המציאות של המערכת הפיזיקלית במלואה. אין מידע נוסף שנסתר מעייננו.
2. פונקציית הגל משתנה בזמן ביחס למשוואה לינארית, תמיד. (למשל משוואת שרדינגר).
3. מדידה של גודל פיזיקאלי מסוים, תמיד תוביל לתוצאה דטרמיניסטית. למשל, אם נמדוד את הספין של האלקטרון, הוא יהיה רק באחת מהאפשרויות – מעלה או מטה.

נוכל להדגים את הסתירה בין הטיעונים בעזרת המתמטיקה של מכניקת הקוונטים. נתמקד באלקטרון עם ספין שאותו נרצה למדוד בציר z. מבלי להיכנס לטבעו של הספין, נניח שלספין קיימים שני מצבים קלאסיים, ״מעלה״ -אותו נסמן עם חץ שמכוון מעלה, ומצב ״מטה״ אותו נסמן כחץ המכוון כלפי מטה. המערכת הפיזיקאלית כולה לא מכילה רק את הספין, אלא גם את מכשיר המדידה. לכן, נוכל לתאר את המערכת והספין ביחד לפני ואחרי המדידה באופן הבא:

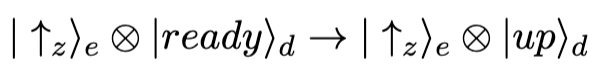
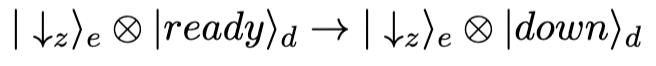
כאן סימנו את המצב של האלקטרון עם האות e בתחתית, ואת המצב של מערכת המדידה (device) באות d. המילה ready מסמנת את המערכת לפני המדידה, ולאחריה מכשיר המדידה משנה את מצבו בהאתאם לספין של האלקטרון. את הספין בחרנו למקם על ציר ה-z כי מכשיר המדידה שלנו מסוגל למדוד את הספין בציר הזה. אם הספין נמצא במצב מעלה נסמנו ב- up ואם מטה נסמנו down.

אך כפי שהזכרנו, מצב קוונטי יכול לערבב כמה מצבים קלאסיים. אם למשל הספין מכוון דווקא בציר איקס, המצב הקוונטי שלו יתואר כסופרפוזיציה של מצבי זד:

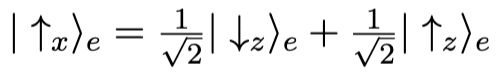
והמערכת כולה תתחיל במצב הקוונטי הבא:

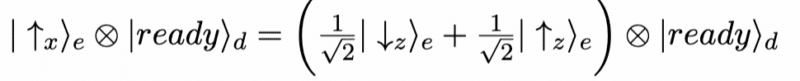
אם הטיעון השני נכון, המצב צריך להתפתח לפי משוואה לינארית, לכן מדידה תוביל לפונקציית הגל להשתנות כך-

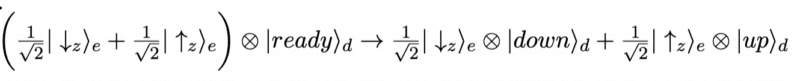
מכאן עולה השאלה, איזה מצב הוא מייצג?

אם הטיעון הראשון נכון, אזי פונקציית הגל צריכה לייצג את כל האפשרויות הפיזיקאליות של המערכת. אבל אז הטיעון השלישי לא יכול להתקיים כי כאן התוצאה היא לא דטרמיניסטית יחידה. פרשנות קופנהגן קובעת שבמקרה זה הסיכוי שנמדוד את החלקיק עם ספין מעלה הוא 50% ובאופן דומה עבור ספין מטה. במילים אחרות הטיעון השלישי לא יכול להתקיים במקרה בו ההתפתחות היא ליארית וכאשר המצב הפיזיקאלי כולו מוגדר על ידי פונקציית הגל.

סתירות אלו הובילו חוקרים להציע מספר פתרונות.

וויתור על הטיעון הראשון, כלומר שפונקציית הגל מתארת את המציאות במלואה מוביל לקיומם של ״משתנים חבויים״. אלו גדלים פיזיקאליים שאין ביכולתנו למדוד ישירות, אך יכולים להשפיע על תוצאות המדידה.

וויתור על הטיעון השני מוביל לתאוריית הקריסה. תורה זו מניחה שמדידה מקריסה את פונקציית הגל לאחת מהאפשרויות הקלאסיות. כדי שתתרחש, ההתפתחות בזמן צריכה להיות לא לינארית, לפחות בחלקה.

תאוריות שמשמרות את הטיעון הראשון והשני אבל לא את השלישי פחות מוכרות. הפופולארית שבניהן היא תאוריית העולמות המרובים של אברט. התאוריה קובעת שבעת מדידה, אין קריסה, פשוט כל האפשרויות קיימות בו זמנית, כל אחת ביקום אחר.

בכל מקרה, כדי לפתור את הקונפליקט חייבים להוסיף פיזיקה חדשה, השאלה איזו? לעיתים בעיית המדידה נתפסת כבעיה פילוסופית בלבד, אבל אני טוען שהתפלספות לא מספיקה. זו בעיה עמוקה יותר שדורשת עיקרון פיזיקלי חדש. כל רעיון שהזכרתי מגובה במתמטיקה רחבה, לא רק פרשנות מילולית. כל תיקון לתורה מעלה שאלות חדשות ולעיתים פרדיקציות מעניינות, כך עובד המדע. יחד עם זאת, הפרשנויות לא חפות מביקורת, ולעיתים הן לא עומדות בקנה אחד עם כל התצפיות. למשל, הפרשנות של בוהם שמוסיפה משתנים חבויים לא משתלבת היטב עם פיזיקה יחסותית.

בעייה שניה – בעיית הסטטיסטיקה

לכאורה נוכל ליישב את הטיעונים שהוצגו מעלה אם נחליט שהמצבים המעורבבים מראים על צג המכשיר תוצאה יחידה. למשל, נוכל לטעון שמצב מעורבב שכזה

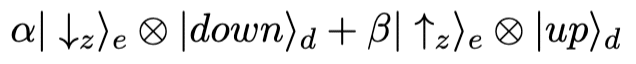
יראה על מכשיר המדידה את התוצאה ״מעלה״ כל עוד בטא גדולה מאלפא ו״מטה״ במקרה ההפוך. הסיבה שאנחנו יכולים לעשות זאת נובעת מהעובדה שלא בהכרח קישרנו ישירות בין פונקציית הגל לתוצאת המדידה. נכון שהמצב הקוונטי של מכשיר המדידה מוגדר כ- ״מעלה״ או ״מטה״, אבל נוכל להתייחס ל״מצב״ כגודל נזיל יותר שלא מכתיב בהכרח את תוצאת המדידה. הבעיה בניסוח החדש שלנו הוא שלפי הכלל של בורן, שאושש ניסויית, עדיין קיימת האפשרות שנקבל את שני האפשרויות כי ההסתברות שהצג יראה מעלה פרופורציונלי למקדם בטא ועבור ספין מטה ההסתברות פרופורציונלית למקדם אלפא.

לכן נסיק ששלושת הטיעונים הבאים לא יכולים להתקיים יחדיו:

1. פונקציית הגל מתארת בשלמות את המציאות.
2. פונקציית הגל משתנה בזמן תמיד לפי משוואה דטרמיניסטית לינארית (משוואת שרדינגר).
3. כאשר מודדים העתקים רבים של אותה פונקציית גל, מקבלים בקירוב טוב את עיקרון בורן.

אם בידנו שתי פונקציות גל זהות, לפי כלל 2, הן חייבות להתפתח בזמן באופן זהה. כך שאחרי אי אלו שניות פונקציות הגל חייבות להישאר זהות. אם הן מתארות בשלמות את המציאות (כלל 1) הן לא יכולות לתאר מדידות שונות, אך זאת בניגוד לכלל 3.

את הסתירה הזו אפשר לפתור למשל בעזרת משתנים חבויים, אך אלו לא באמת חבויים, אחרת לא הייתה להם השפעה כלל. בדרך כלשהי, הם צריכים להתהוות במדידה, אחרת לא נוכל לקבל שתי תוצאות שונות מאותה פונקציית גל. אלו המאמינים בהתפתחות לא לינארית טוענים שהיא בעצמה לא דטרמיניסטית. במילים אחרות, שתי פונקציות גל שאותחלו באופן זהה לא יראו אותו הדבר אחרי זמן מה. לעומתם, אלו המתכחשים לכלל 3, כלומר אלו המאמינים בעולמות מרובים, עשויים להיתפס ככאלו שמתכחשים לתוצאות אמפיריות. יחד עם זאת, אלו יגידו שלמעשה מדידה כלל לא מתרחשת וכל האפשרויות קיימות במקביל.

בעיה שלישית – בעיית האפקט

הבעיה השלישית נובעת מהמדידות הבאות. אם האלקטרון התחיל במצב מעורבב, הפרשנות של בורן טוענת שאחרי המדידה הוא יקרוס לאחד מהמצבים הדטרמיניסטיים – מעלה או מטה. הקריסה משנה ממש את פונקציית הגל ובמדידות הבאות הספין ישאר באותו הכיוון כי כל ההסתברויות האחרות קרסו לאפס. זו ״בעיית האפקט״, תופעה שמשמרת את האינפורמציה של המדידה הראשונה גם במדידות עתידיות. אלו המצדדים בדינאמיקה לא לינארית לא נתקלים בבעיית האפקט. הדינאמיקה משמרת את המצב אחרי שהוא קרס. לעומת זאת, בתורות שבהן אין קריסה כמו זו שניסח בוהם (משתנים חבויים) הבעיה יכולה לצוץ. אם אין קריסה, איך המערכת שומרת את התוצאה של המדידה הקודמת? הפיתרון שהציג בוהם לבעיית האפקט מוחבא באותם משתנים חבויים ששומרים על המידע בהתנהגותם הקלאסית. מבלי להיכנס לקשת הפרשנויות שקיימות בספרות אציין שלא כולן מקיימות את הקריטריון הזה, ובלעדיו להערכתי אין לפרשנות צידוק.

אם כך – מה הפרשנות האמיתית?

לאחרונה פורסם סקר במגזין נייצ׳ר ששאל פיזיקאים מרחבי העולם מהי הפרשנות האהובה עליהם. הפרשנות של קופנהגן זכתה ב-36% אחוזים בקרב המצביעים, רק 15% הצביעו בעד עולמות מרובים ו-7% בעד בוהם. אגב, 17% הצביעו בגישה האפיסטמית שלפיה פונקציית הגל תלויה בצופה והיא רק תיאור מתמטי של מה שעשוי לקרות לאחר המדידה.

כשנשאלו מהי פונקציית הגל 47% אחוזים טענו שאין לה ייצוג ממשי בטבע, 19% טענו שהיא רק תיאור חלקי של המציאות, 17% סברו שמדובר בתיאור מלא של המציאות, 8% טענו שהיא מתארת אפקט סובייקטיבי של הנסיין ול-8% לא היה מושג.

בשאלה האם נדרש צופה למדידה, 9% ענו כן, והוא חייב להיות בעל תודעה, 56% ענו שכן, אבל הוא לא חייב להיות בעל תודעה, גם אינטראקציה עם הסביבה יכולה להחשב כמדידה, 28% ענו לא ו-8% ענו לא יודעים.

הסקר הזה מדהים בפני עצמו. רק שליש מהפיזיקאים מסכימים עם פרשנות קופנהגן. זו סטירת לחי בפני הממסד שמלמד דורות של פיזיקאים על בסיס הנחה זו. העובדה שאין הסכמה גורפת מוכיחה לכולנו שמכניקת הקוונטים עדיין לא ברורה לנו, גם 100 שנים אחרי. לצד זאת, ואולי המפתיע מכל, זה לא הפריע למדענים לגלות תופעות חדשות, לחקור את המבנים היסודיים ביותר ולהעמיק את הידע שלנו על העולם. אבל אני שואל, האם איי פעם נגיע לרוויה, והאם דלתות חדשות יפתחו רק אם נסדיר בעיה עמוקה הזו?

מוזמנים לעיין בעוד כתבות בבלוג שלי ״למה הקוונטה״. יש לכם שאלה? רוצים שאכתוב על נושא שמעניין אתכם? פנו אליי לכתובת המייל: [email protected]
אתם מוזמנים גם לעקוב אחרי גם ב-BlueSky כדי להתעדכן על הרצאות לקהל הרחב.

עוד בנושא באתר הידען:

• אז מה עושים שם באוניברסיטה? פרק 4: לא עוצר בצהוב – על אופטיקה לא לינארית
• "על סטודנטים ובוגרי מדעי המחשב לעשות הסבה לתכנות קוונטי, כי זה העתיד"
• תורת הקוונטים משפיעה על תהליך פליטת האור
• האם כבידה פותרת את בעיית המדידה?
• הקשר שנשלל בין הקוונטים לתודעה