הייתכן כי הטבע פספס גביש?

החיפוש אחר גביש K4 שדומה בסימטריה שלו ליהלום. האם קיים בטבע או אולי ניתן ליצור אותו במעבדה?

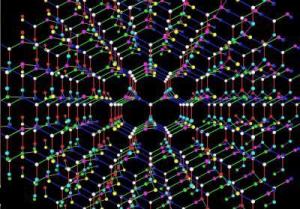
במשך מאות בשנים, בני-האדם הוקסמו מהנצנוץ שובה-הלב של היהלום. מה ההסבר ליופי המרשים של אבן-החן יקרת-הערך הזו?

כפי שמסביר המתמטיקאי טושיקאזו סונאדה במאמר המתפרסם בכתב-העת האמריקאי Notices of the American Mathematical Society, חלק מרזי היופי של היהלום יכולים להיחשף על ידי ניתוח מתמטי של המבנה המיקרוסקופי של הגביש. מתברר כי למבנה זה תכונות מיוחדות, בייחוד סימטריה גבוהה. למעשה, כפי שגילה החוקר, מתוך מאגר אינסופי של גבישים “מתמטיים” רק אחד אחר הוא בעל תכונות סימטריה משותפות ליהלום, גביש אותו הוא מכנה “גביש K4”. עדיין לא ברור אם אכן קיים גביש מסוג זה בטבע או באם ניתן להכינו במעבדה.

אפשר לבנות דגם מתמטי מושלם של גביש על ידי התמקדות במאפייניו העיקריים, דהיינו, מיקום האטומים השונים והקשרים ביניהם. האטומים מיוצגים ע”י נקודות, אותן נכנה “קודקודים”, והקשרים מיוצגים על ידי קווים, אותם נכנה “קטעים”. סוג זה של מערך המורכב מקודקודים וקטעים מכונה תרשים. הגביש הולך ונבנה תחילה על ידי שלד-ראשוני של תרשים וחיבור העתקים מושלמים נוספים שלו יחדיו באופן מחזורי. כלומר, ישנן שתי תבניות הפועלות בגביש: תבנית הקטעים המחברים את הקודקודים השונים בתרשימי השלד-הראשוני (הווה אומר – מערך הקשרים שבין האטומים), והמערך המחזורי המחבר את ההעתקים של התרשימים. ניתן לקבל אינסוף מבנים מתמטיים של גבישים בדרך זו, על ידי שינויים בתוך התרשים הראשוני ושינויים בצורת החיבור של העתקי התרשימים.

לגביש היהלום ישנם שני מאפייני-מפתח המבדילים אותו משאר הגבישים. הראשון, המכונה “סימטריה מרבית”, מתייחס לסימטריה של סידור תרשימי השלד הראשוני. חלק מהסידורים סימטריים יותר מאחרים, ואם מתחילים מסידור מסוים, ניתן לעוות אותו תוך שימור המחזוריות והקשרים שבין האטומים לקבלת מבנה סימטרי יותר. עבור גביש היהלום, מתברר כי אין שום עיוות בסידור המחזורי המסוגל להביא לקבלת מבנה סימטרי יותר. כפי שמציין החוקר, ליהלום יש את הסימטריה המרבית האפשרית. ניתן לעוות כל גביש לקבלת גביש בעל סימטריה מרבית, כך שמאפיין זה לבדו אינו ייחודי ליהלום. אך ליהלום יש מאפיין מפתח נוסף, המכונה “המאפיין האיזוטרופי החזק”. [“איזוטרופיות” היא אי תלות בכיוון. איזוטרופיות חשובה במספר תחומים כגון: מתמטיקה, פיזיקה, אופטיקה, פיזיולוגיה ותכונות חומרים. לדוגמה, היקום הוא איזוטרופי – אין בו נקודה מיוחסת או ייחודית, או כיוון מועדף כלשהו. גם קרינת הרקע מגיעה במידה שווה מכל הכיוונים – היא קרינה איזוטרופית]. תכונה זו דומה לסימטריה הסיבובית המאפיינת את המעגל והכדור: לא משנה לאיזה כיוון תסובב אותם – הם ייראו אותו הדבר. ליהלום תכונה דומה, כך שהגביש נראה זהה במבנהו מכל צד שנסתכל עליו.

מסתבר, כי מכל מאגר הגבישים הנבנים בצורה מתמטית, רק לאחד נוסף יש את שני מאפייני-המפתח המסוימים הללו של היהלום. החוקר מכנה אותו “גביש K4”, כיוון שהוא מורכב מתרשים הקרוי K4, המכיל ארבע נקודות כאשר כל זוג מהן מחובר על ידי מקטע. “גביש ה-K4 אינו נופל ביופיו מזה של היהלום,” טוען החוקר. “מבנהו האומנותי סיקרן אותי זה זמן רב”. הוא מציין כי למרות שהגביש הנ”ל קיים רק כחישוב מתמטי, מפתה לתהות אם הוא יכול להתגלות בטבע או להתקבל במעבדה. הדבר אינו כה מופרך – הפולרן, חומר שצורתו כצורת כדורגל מושלם (כינויו הטכני – איקוזאהדרון קטום), חושב מתמטית הרבה לפני גילויו בטבע, בשנת 1990, כפרודה C60.

מאמרו של סונאדה, “גבישים שהטבע אולי החמיץ לברוא”, מופיע בגיליון פברואר 2008 של AMS Notices והועלה לרשת בשלושה בינואר.

להודעת החוקרים