השנה זכו שלושה חוקרים מאוניברסיטת סנטה ברברה על סדרת ניסויים פורצי דרך שביססו את הקיוביט העל־מוליך – הרכיב המרכזי שמדענים ברחבי העולם משתמשים בו כיום כדי לבנות מחשבים קוונטיים. בכתבה אסקור כיצד רעיון תאורטי ממכניקת הקוונטים הפך לניסוי ממשי בצמתי ג׳וספסון, מהו מנהור מאקרוסקופי ומה אפשר בזכותו את בניית הקיוביט העל־מוליך – היסוד שעליו נשען המחשוב הקוונטי כולו.
השנה הוענק פרס נובל לפיזיקה לשלושה חוקרים מאוניברסיטת סנטה ברברה, קליפורניה (ארה״ב): ג׳ון קלארק, מישל דבורה וג׳ון מרטינס על מנהור קוונטי מאקרוסקופי ועל ״קווינטוט״ מעגלים חשמליים. בשנים האחרונות וועדת הפרס רודפת אחר טרנדים. בשנה שעברה למשל, הפרס הוענק לקבוצת חוקרים בתחום הבינה המלאכותית. השנה, מכניקת הקוונטים היא התורן הלוהט. בחגיגות המאה שמצוינות ברחבי העולם, המונח ״מחשב קוונטי״ נזרק לכל עבר ונשמע עד כותלי האקדמיה השוודית. מצד אחד, היא מרגישה מחויבת לזכות את התחום בפרס, מצד שני היא יודעת טוב מאוד שמחשבים קוונטים עוד לא הוכיחו את עצמם. הפיתרון אם כך הוא פשוט: נעניק פרס על מחשוב קוונטי בהסוואה. הכותרת תהיה על תופעה יסודית לכאורה במכניקת הקוונטים, אבל בין השורות ברור שהפרס הוענק עכשיו בגלל אירועי השנה. יחד עם זאת, אין ספק שהפרס ראוי ושהתגליות הובילו לשורת פיתוחים טכנולוגיים.
הרעיון המדעי
ובחזרה לרעיון המדעי שזיכה את החתנים בפרס. אפקט המנהור נוסח עוד מראשיתה של מכניקת הקוונטים, כשארווין שרדינגר, המדען האוסטרי הציג לעולם את משוואת הגלים המפורסמת שתיארה את האופי ההסתברותי של העולם. הפיזיקה הקלאסית מלמדת שאותם חלקיקים, שלרוב מתוארים ככדורים קטנטנים, אינם מסוגלים לעבור דרך מחסומים פיזיים כמו קירות. אם נזרוק כדור לקיר, הוא ישנה את מסלולו ויחזור חזרה אלינו משום שברגע המפגש, אותם חלקיקים המרכיבים את כדור והקיר דוחים חשמלית אחד את השני. אפשרות נוספת היא שהכדור מספיק אנרגטי כדי לשבור את הקשרים החשמליים בין האטומים שמרכיבים את הקיר וליצור בו סדקים. בכל מקרה, אם נזניח את האפשרות שהכדור מסוגל לשבור את הקיר, הוא לא יחדור אותו לעולם. (נוכל לדמיין אפשרות שלישית בהנחה שגובה הקיר סופי. אם נזרוק את הכדור מספיק גבוה, לכדור יהיה מספיק אנרגיה לדלג מעל הקיר, אבל זו לא הדרך הקוונטית שעליה נדבר בהמשך).
לעומת זאת, אם הכדור היה מיקרוסקופי – בגודל של חלקיק יחיד – הפיזיקה הקלאסית כבר לא הייתה רלוונטית. במקרה כזה, התנהגות החלקיק נקבעת על פי מכניקת הקוונטים, שיכולה לנבא הסתברות סופית לכך שהחלקיק יצליח לעבור את הקיר, גם אם אין לו מספיק אנרגיה לעשות זאת באופן קלאסי. ההסתברות אומנם קטנה ככל שהקיר עבה יותר, אבל אם האנרגיה של החלקיק מספיק גדולה (אך עדיין לא גדולה מספיק שגם קלאסית היא תהיה מסוגלת לעבור לצד שני) והעובי של הקיר סופי, ההסתברות שהחלקיק פתאום יופיע בצידו השני של הקיר אינה אפסית. זהו אפקט המנהור הקוונטי. השם מנהור מלשון מנהרה, כדי לדמות (ציורית כמובן) שהחלקיק חודר את המחסום האנרגטי דרך מנהרה.
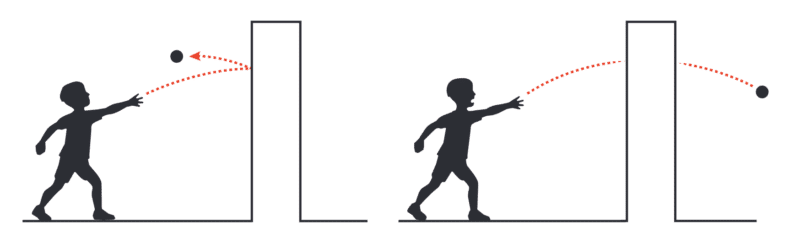
במקביל לרעיונות היסוד שפותחו במכניקת הקוונטים, התגלו חומרים בעלי תכונות קוונטיות יוצאות דופן – כמו על מוליך הנצפות בטמפרטורות נמוכות מאוד. כאשר החומר הופך לעל-מוליך, הוא מסוגל להוליך חשמל בלי התנגדות והזרם החשמלי שזורם בו לא יעצור כל עוד העל מוליך נשמר בטמפרטורה נמוכה. התכונה הקוונטית סקרנה חוקרים רבים שדמיינו עולם ירוק וחסוכני בו מוליכים פשוטים מוחלפים בעל מוליכים. בשנות השישים של המאה הקודמת הפיזיקאי בריאן ג׳וספסון גילה שאם מחברים שני על מוליכים בעזרת מבודד חשמלי, זוגות אלקטרונים יכולים להתמנהר דרך המבודד מעל מוליך אחד לאחר. למערכת זו קוראים היום צומת ג׳וספסון. הניסוי של ג׳וספסון הוביל להמצאת ה-SQUID, מכשיר שמבוסס על מנהור כדי לסרוק אטומים בחומר ולצלם אותם. על תגלית זו ג׳וספסון זכה בנובל לפיזיקה בשנת 1973 יחד עם שני חוקרים נוספים בתחום העל מוליכים.
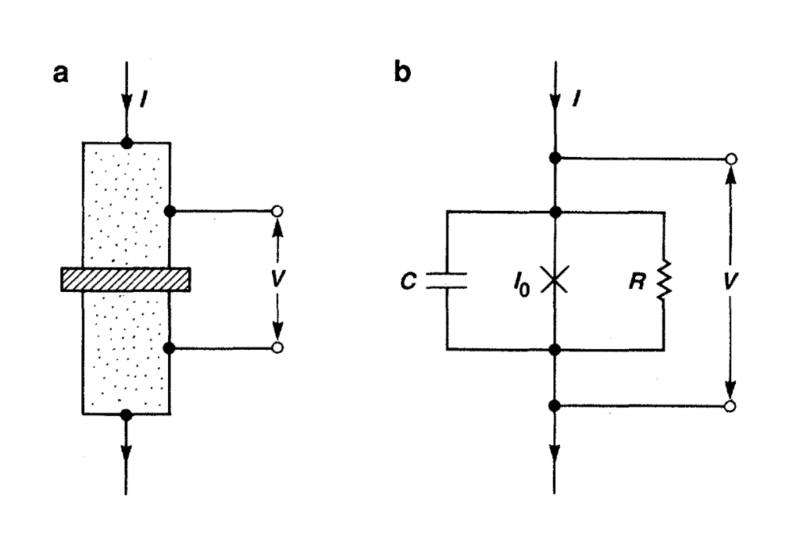
נזכור שכל על מוליך נמצא במצב קוונטי משלו. בגדול, המצב הקוונטי מתאר את מספר האלקטרונים המשתתפים בו. למצב הקוונטי של העל מוליך יש תכונה נוספת שהיא אוסילטורית (מחזורית). שני העל מוליכים יכולים להתנדנד באופן בלתי תלוי באחר. בדומה לגלים מתנדנדים -העל מוליכים יכולים להתנדנד יחד, כלומר להתחיל ולסיים באותה פעימה, או לא להיות מחוץ לסנכרון.
מידת אי ההתאמה מכונה ״הפאזה שבין העל מוליכים״. כששני העל מוליכים בסנכרון מושלם הפאזה שווה לאפס, כשהם בסנכרון הפוך, הפאזה שווה לפאי.
הפאזה בניהם נשלטת על ידי הזרם שזורם בצומת, ואם הפאזה פתאום משתנה, נוצר מתח בין חלקי הצומת והמערכת אינה על מוליכה יותר. לעומת זאת, במצב היציב, זורם זרם חליפין בין שני חלקי הצומת, הפאזה לא משתנה ואין מתח. משום שזו מערכת קוונטית, באופן רנדומלי, הפאזה יכולה להשתנות בעזרת מנהור. זהו לא מנהור ״קלאסי״ של חלקיק בודד, אלא מנהור בפאזה היחסית של שני חלקי העל מוליך. מדוע זהו מנהור? כדי לשנות את הפאזה נדרשת אנרגיה, אך במצב בו הפאזה יציבה, לאלקטרונים בעל מוליכים אין מספיק אנרגיה לשנות אותה. יחד עם זאת, עדיין קיימת הסתברות שצומת ג׳וספסון תתקיים במצב עם פאזה אחרת, כלומר שהיא תחצה את מחסום אנרגיה ותתייצב על מצב פיזיקאלי חדש.
המנהור בין שני פאזות שונות מערב למעשה תיאום בין כמות עצומה של מיליארדי אלקטרונים, ולכן הוא מכונה מנהור מאקרוסקופי.
על הניסוי של זוכי הנובל
בשנות השמונים פרסמו שלושת זוכי הנובל מאמר פורץ דרך בכתב העת Physical Review Letters בו הדגימו לראשונה מנהור מאקרוסקופי בצומת ג׳וספסון, ראו גרף:
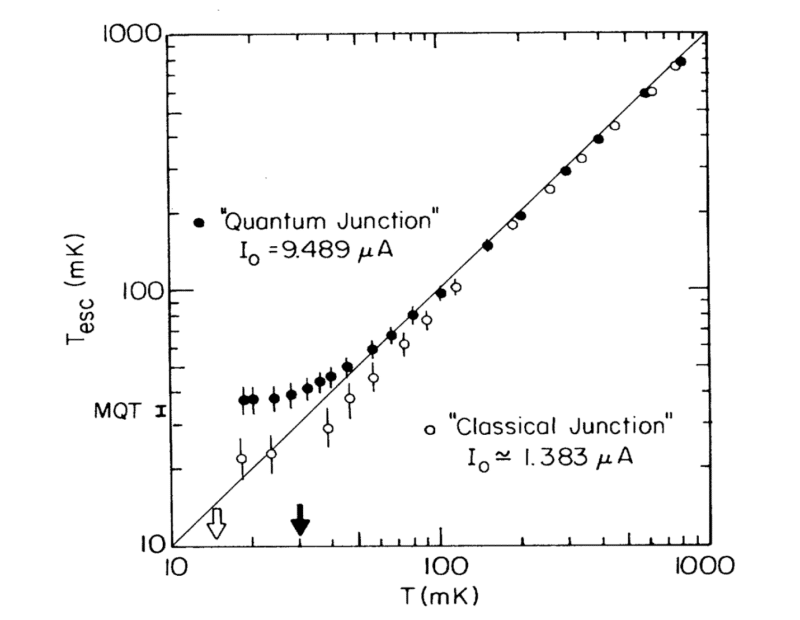
הם קיררו את הצומת לטמפרטורות שונות ומדדו את ההסתברות שהפאזה תשתנה. אילו התהליך היה קלאסי, ההסתברות לשינוי הייתה פוחתת בהתמדה עם ירידת הטמפרטורה, משום שלמערכת פחות אנרגיה זמינה. אולם בטמפרטורות נמוכות מאוד הופיע “זנב” מובהק בגרף – עדות לכך שההסתברות איננה נעלמת, ועדות לכך שמנהור קוונטי תורם למעבר הפאזה גם ללא אנרגיה תרמית.
מעבר לכך, החוקרים הדגימו שהארגיה האגורה בצומת בכל מצב מטא-סטבילי של הפאזה היא מקוונטטת, ממש כמו באוסילטור הרמוני קוונטי. במילים פשוטות, קיים סט בדיד של אוסילציות בזרם שלכל אוסילציה שכזו משויכת אנרגיה בדידה. הצומת חייב להימצא באחד מסט המצבים האלה ולא במצב ביניים. האוסילציות בזרם ידועות בתור זרם חליפין, ובמקרה הזה, הזרם החליפין הוא בעל מוליך.
שימושים
כיום, מחשבים קוונטים רבים בנויים מהמון צמתי ג׳וספסון. העובדה שניתן ליצור אוסילטור הרמוני קוונטי בעזרת על מוליכים אפשרה לפיזיקאים ליצור קיוביטים נשלטים. קיוביט הוא כינוי לכל מערכת פיזיקאלית שיש לה שני מצבים מבודדים הנבדלים באנרגיה. באוסילטור הרמוני למשל יש שני תנודות מרכזיות, תנודה עם אנרגיה מינימלית המכונה מצב היסוד, ותנודה אנרגטית הנושאת מנת אנרגיה אחת. את מצב היסוד לרוב מסמנים במספר 0 (כי הוא לא נושא שום תוספת אנרגטית) והמצב השני במספר 1 (כי יש לו תוספת של מנת אנרגיה אחת). אותם מצבים 0,1 מקבילים למצב הבינארי הקלאסי במדעי המחשב. בזכות אופיו הקוונטי, הקיוביט יכול להיות בסופרפוזיציה של שני המצבים ואף בשזירה עם קיוביטים אחרים – תכונות המאפשרות ביצוע חישובים קוונטיים.
ניתן לממש קיוביטים במגוון שיטות, אך צמתי ג׳וספסון הם מהנפוצים והיעילים ביותר בזכות העובדה שניתן לשלוט ברכיבים חשמליים בצורה מדויקת מאוד. לכן, לא מפתיע שהפרס השנה ניתן בדיוק לאלה שהניחו את היסודות הניסויים לתחום כולו.
מוזמנים לקרוא כתבות נוספות בבלוג שלי ״למה הקוונטה״. יש לכם שאלה? רוצים שאכתוב על נושא שמעניין אתכם? פנו אליי לכתובת המייל: [email protected] אתם מוזמנים גם לעקוב אחרי גם ב-BlueSky כדי להתעדכן על הרצאות לקהל הרחב.
עוד בנושא באתר הידען:
