בשנת 2010 אדוארד וויטן העביר הרצאה לקהל הרחב מטעם IAS (המכון ללימודים מתקדמים בארה"ב) על תורת הקשרים ומכניקת הקוונטים. בכתבה זו נעביר את עיקרי דבריו עם הרחבות נקודתיות. על פניו, תורת הקשרים התחילה כמו עוד "תעלול" מתמטי, אך כמו רוב התגליות המדעיות, המתמטיקאים הקדימו את הפיזיקאים בכמה עשורים

קשירה ופרימה הן פעולות שגרתיות. מידי יום רבים מאיתנו קושרים את שרוכי הנעליים במטרה לאפשר לשרוך לעשות את עבודתו – לחבר בחוזקה את צידי הנעל. מידי פעם הקשר בא לרעתנו- מי מאיתנו לא חווה את תחושת התסכול כאשר גילה שהאוזניות החוטיות שבכיסו נכרכו זו בזו או שהתכשיט העדין שזה עתה קנה התלפף בטבעיות ויצר קשרים הדוקים. האתגר כמובן הוא לפרום את הקשרים, דבר הדורש מאמץ רב והמון זמן.
עבור המתמטיקאים, המונח "קשר" הוא יותר אבסטרקטי אך בסך הכול הוא מתאר לולאה מלופפת המרחפת בחופשיות במרחב-זמן. דוגמא בסיסית לקשר מופיע באיור מספר 1, אני מקווה שהאיור מזכיר לכם חוט מלופף מחיי היומיום. אם התמונה מבלבלת, אל דאגה אתם ממש לא היחידים. מתמטיקאים רבים מתקשים להבין כיצד קשרים מלופפים וכיצד ניתן להשוות בניהם. רבים מאיתנו (ולא רק המתמטיקאים) רוצים לדעת מראש אילו קשרים בלתי ניתנים לפרימה לפני שמתחילים בעבודה הקשה (חבל על המאמץ מן הסתם). זו שאלה ממש לא טריוויאלית ולכן היא מהווה מוטיבציה חיובית לבניית תורת הקשרים.
אבל רגע, לפרום קשרים? איך כל זה קשור למתמטיקה? לאוזני אלו הרגילים לחשוב שמתמטיקה היא לא יותר מאשר חיבור חיסור כפל וחילוק צצות במוחם לא מעט סימני שאלה. למעשה, במאה העשרים מתמטיקאים בנו תורה יסודית ועמוקה רק על קשרים. אבל מדוע, מעבר להנאה הברורה מפתרון חידות משעשעות, פיזיקאים מתעניינים בתורת הקשרים? ההתעניינות החלה מכמה תגליות מפתיעות לפני כמה עשורים וכדי לתאר אותן כמו שצריך, נתחיל עם הסבר פשוט על "פולינומי ג'ונס" שהתגלו בשנת 1983. המפתיע הוא שניתן להסביר את הרעיון גם לתלמידי תיכון, דבר שכמעט אינו קיים במתמטיקה מודרנית. כדי להמחיש עד כמה זה מפתיע תחשבו על ההסתברות שמישהו ינסה להסביר את המשפט האחרון של פרמה לנערות ונערים בני 16.

לשם פשטות נטען שג'ונס חיבר לכל קשר מספר (או פולינום). נניח שיש בידינו קשר כלשהו בשם K ונתאר את המספר ג'ונס הקשור לו בסימון JK. כדי לחשב את מספר ג'ונס כל מה שצריך לעשות הוא להפעיל את המתכון הבטוח שעם לא מעט סבלנות, נוכל לחשב את ערכו. אם JK שווה ל-1 נגדיר שאין שום קשר בלולאה (איור 2).

כל מספר שאינו אחד ירמוז שהקשר K אינו ניתן לפרימה. במילים אחרות, אם נחזור לקשר באיור 1, כמעט בלתי ניתן לדעת כיצד הקשר הזה ניתן לפרימה, אבל בזכות ג'ונס ניתן לקבוע עובדה זו, פשוט יש לחשב את ערכו של JK . אם הוא שונה מאחד, לא ניתן לפרום את הקשר. הדרך שג'ונס הגיע לערכו של JK מתוחכמת מאוד, אך מרגע שיש בידינו את הדרך, לא צריך להיות מתוחכם כדי לחשב אותו. למען האמת ישנן לא מעט דרכים לחשב את מספר ג'ונס, ובמאמר זה נראה דרך אחת. עבור כל קשר שאינו איור 2, נצטרך "לשחק" את המשחק הבא – בחרו את שלושת המספרים האהובים עליכם, נניח 2,3,5. כעת נתבונן בקשר החלקי (איור 3), הוא חלקי משום שיש בו חלק חסר.

אם לרגע חושבים על זה, קיימות שלוש אפשרויות להשלמת החלק החסר (איור 4).
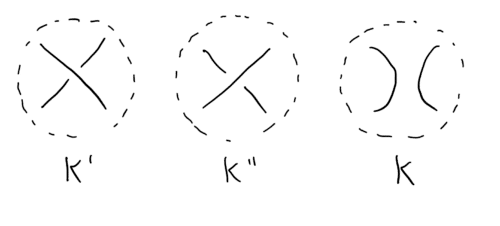
נסמן כל אופציה בתור K, K',K". ג'ונס הראה שעבור שלוש אפשרויות קיים הקשר הבא:
2 JK + 3 JK' + 5 JK" = 0.
אם מבצעים איטרציות רבות על ליפופים נוספים בקשר זה, בסופו של דבר ניתן לחשב את JK המקורי.
השיטה שתיארנו כאן מצליחה ביעילות רבה לחשב את JK, אך מדוע היא נכונה? לצערי, קשה להסביר לאלו שאינם מתמטיקאים או פיזיקאים מדוע המתכון עובד. שאלו מסוג "מדוע" בד"כ מושכות אנשים ללמוד מתמטיקה, ואם בזה הרגע שאלתם את השאלה הזו, אולי כדאי לכם ללמוד את התחום בעתיד. מיד עם גילוי פולינומי ג'ונס, מתמטיקאים רבים חשפו עוד קשרים יוצאי דופן, כאלו שלא היה להם הסבר מעמיק. למרות הכול, הרמז ריחף באוויר. למען האמת, היו לא מעט רמזים, בעיקר מכיוונה של הפיזיקה המתמטית. עם השנים הסתבר שלתורת הקשרים חיבור עמוק עם תורת הקוונטים, לכן נסביר בקצרה כיצד מכניקת הקוונטים שונה מהמכניקה הקלסית.
על פי המכניקה הקלאסית, חלקיק הנע מנקודה אחת לשנייה נע על מסלול יחיד המוגדר על פי הכוחות הפועלים עליו (איור 5) בהתאם לחוקי ניוטון.
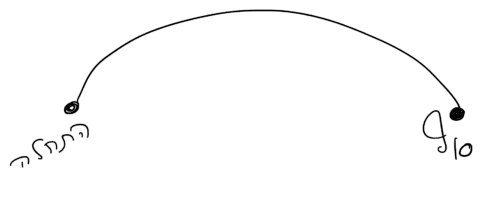

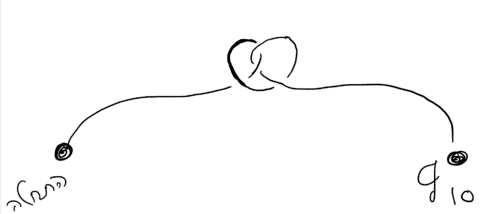
לעומתו, על פי העיקרון של פיינמן, חלקיק קוונטי יכול לנוע בכל מסלול, מוזר ככל שיהיה. הוא יכול לנוע במסלול הקלאסי אבל גם במסלול זיגזגי כמו באיור 6. לכל מסלול, משויך מספר, או ליתר דיוק הסתברות בה החלקיק ינוע על מסלול זה. משום שחלקיק קוונטי יכול לנוע בכל מסלול אפשרי, הוא גם יכול לנוע על מסלול קשור ומלופף כמו באיור 7. פיזיקאי קוונטי מנוסה יודע לתרגם כל מסלול להסתברות, גם מסלול כמו זה שמופיע באיור 7 או 6, אם כי הם פחות סבירים מהמסלול הקלאסי. החישוב דורש מאמצים רבים וכלים אנליטיים עוצמתיים. בגדול, ההסתברות לכל מסלול K ניתנת לחישוב על ידי אופרטור ווילסון שנסמנו ב-Wk. במסגרת המאמר, לא נוכל להגדירו בפשטות, אך לכל צורך מעשי נאמר שאופרטור וילסון הוא כלי חשוב ויסודי בתורת הקוונטים, למשל הוא משמש לתיאור עוצמת הכוחות בין הקוורקים. אם כך, מסתבר שהקשר בין פולינומי ג'ונס לתורת הקוונטים נובע מהעובדה שהממוצע הקוונטי של אופרטור וילסון על מסלול מלופף K הוא JK ! זו תוצאה פשוטה ונפלאה בהתחשב בעבודה שנדרש מאמץ אנליטי רב לחישוב כל הסתברות.
התיאור הנפלא והמפתיע מגיע גם עם כוכבית ליד – הקשרים שאנחנו רגילים לדמיין קיימים במרחב תלת מימדי, אבל כאשר לוקחים בחשבון את תורת הקוונטים, חייבים להניח שהקשרים מרחפים במרחב-זמן. לשם כך, חובנוב פיתח מתמטיקה לא טריוויאלית המרחיבה את פולינומי ג'ונס למרחב תלת ממדי ביחד עם ממד זמני. הרעיון של חובנוב הוא יותר אבסטרקטי ממספר שמתאר את הקשרים וליפופים. למעשה חובנוב חיבר בין מצבים קוונטים לליפופים ובעזרתן ניתן לחשב תכונות ייחודיות של חומרים בטבע. ליתר דיוק, המסלולים הקשורים והמלופפים שחלקיקים נעים חשובים מאוד בתורת שדות קוונטית טופולוגית, וכדוגמא לכך מודל צ'רן סיימונס נחשב להצלחה הבולטת ביותר בשנים האחרונות. על המודל ניתן לכתוב סדרת כתבות נפרדת אבל אם נתייחס בקצרה, המודל לוקח בחשבון תכונות טופולוגיות ייחודיות שבעזרתן ניתן להסביר למשל את אפקט הול השברי.
לסיכום, המתמטיקה לרוב מקדימה את הפיזיקה, אבל ממש כמו תורת הקשרים ומכניקת הקוונטים היופי האמיתי מתגלה כאשר המתמטיקה מצליחה לתאר את העולם הפיזיקאלי.
להרצאה המקורית ביוטיוב
עוד בנושא באתר הידען:

2 תגובות
רוב החלקיקים ינועו מנקודה לנקודה כמו באיור 5
ישנם חלקיקים עם רצון, יכולת ושאיפות ואלה ינועו מנקודה לנקודה בדרך עקלקלה אחרת ולא צפויה – כי הם רוצים ויכולים
בדומה לג'ונתן ליווינגסטון השחף – חלקיקים אלה חוברים לדומיהם ויוצרים את היקום הצבעוני, המעניין והמוכר לנו
ישנם גם חלקיקים אובייקטיביים שצופים מהצד ומעת לעת בוחרים מסלול תנועה, כלומר את הדרך מנקודה לנקודה
חלקם נשארים כצופים(spectators), חלקם רוצים לנוע כמו באיור 5 ללא מאמץ, חלקם בוחרים לנוע אחרת ונכשלים
וחוזרים לצפות מהצד עד הדחף הבא, חלקם מנסים שוב ושוב ושוב וברצף עד שמצליחים לנוע במסלול שבחרו
ואלה בעלי הרצון והיכולת והשאיפה מצליחים לחבור מיד לדומיהם ויוצרים קשרים מתנועתיים מורכבים…. ונהנים
באיור 4 יש עוד אפשרות פשוטה. כמובן שיש עוד אינסוף אפשרויות מסובכות – ליפוף של החוטים פעם, פעמיים, מליון פעמים.