מושגי יסוד בפיזיקה קוונטית: היכן הקוונטום?

היכן הקוונטום במכניקת הקוונטים? מסתבר שהטבע כלל לא בדיד, כל עוד אין מה שיאלץ אותו להיות כזה

פיזיקה קוונטית מעלה אסוציאציות רבות. בדרך כלל, אלו שאינם בקיאים בתחום יניחו שמדובר בתיאור בדיד של הטבע. משפטים כמו “הכול מגיע במנות”, “קוונטים= חלקיקים?”, “היקום בדיד ואינו רציף”, וגם “חלקיקים הם גלים ולהיפך” הפכו להסברים קאנונים שגורמים לבלבול ואי נוחות. נכון שישנם גדלים המוגבלים לקבל ערכים בדידים אבל למעשה, אם מתבוננים במשוואות המכתיבות את הדינאמיקה של החלקיקים, לא רואים שום סימן לאופי הבדיד של היקום. מה הכוונה במשפט האחרון? מכניקת הקוונטים כולה נשענת על פונקציית הגל שמאגדת את סך ההסתברויות להימצא בכל במצב בטבע (במילים אחרות, פונקציית הגל היא בסך הכול סכום פשוט של מצבים, לדוגמא a*מצב1+b*מצב2 כאשר המקדמים a,b בערך מוחלט בריבוע יתארו את ההסתברות להימצא במצב). פונקציית הגל מתפתחת בזמן לפי משוואת שרדינגר. אם נזכר במשוואה (הרחבה על משוואת שרדינגר ניתן למצוא בכתבה הקודמת) נראה שהיא רציפה לחלוטין משום שנגזרת דורשת מרחב חלק (במיקום ובזמן). ממשוואה זו אנחנו לא יכולים לדעת מראש אם פונקציית הגל מתארת מספר בדיד או מרחב רציף של אפשרויות. ובכל זאת, לא חסרות דוגמאות לכך שגדלים מדידים בטבע מוגבלים לערכים בדידים. למשל “רמות האנרגיה” או המסלולים האפשריים של האלקטרון הקשור לגרעין האטום אינם פרמטרים רציפים, כלומר ניתן למנות אותם והם מופרדים במרחק סופי אחד מהשני. מהיכן אם כך הגיע לפתע היקום הבדיד?

הכול מתחיל ונגמר בגלים. תחילה, שימו לב למושג “אלקטרון קשור” שציינו לפני כן. אם האלקטרון הוא חופשי לחלוטין, כלומר לא פועלים עליו כוחות, אין סיבה שהאנרגיה שלו תופיע במנות בדידות, או במילים אחרות אין סיבה שהאלקטרון ינוע במסלולים מוגבלים בלבד. העובדה שלאלקטרון מסלולים מותרים ואסורים נובעת בעיקר מאילוץ כלשהו. בגלל שהנוסחאות המתמטיות של פונקציית הגל זהות מאוד למכניקת הגלים, ננסה לדמיין מערכת קלאסית גלית שתקביל לזו הקוונטית. בהינתן מיתר הקשור בקצותיו, ניתן לעורר בו גלים עומדים בכל מיני תדרים.

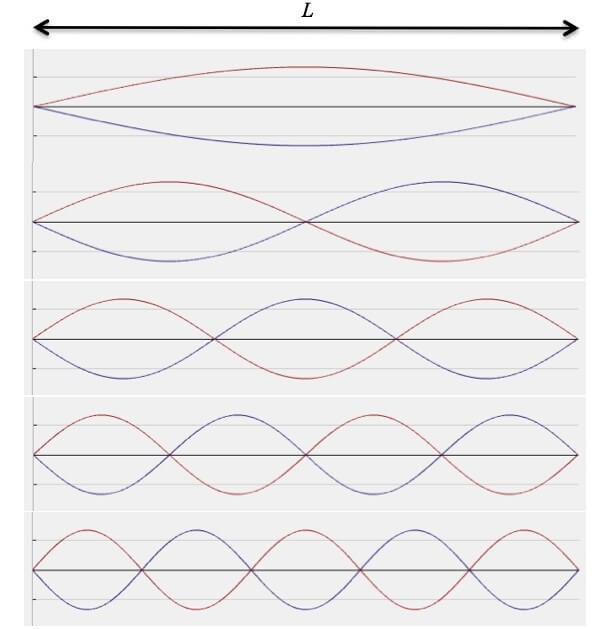
גל עומד מבחינתנו יתאר חלקיק עם אנרגיה מוגדרת, משום שעבור גל עומד ניתן להגדיר תדר ייחודי וכל תדר מגדיר אנרגיה לחלקיק מעיקרון הדואליות (דואליות גל-חלקיק). אבל אם נערוך את הניסוי על מערכות אידאליות שכאלה נראה שאיננו מסוגלים לעורר כל תדר שנרצה על המיתר. התדרים המותרים יהיו:

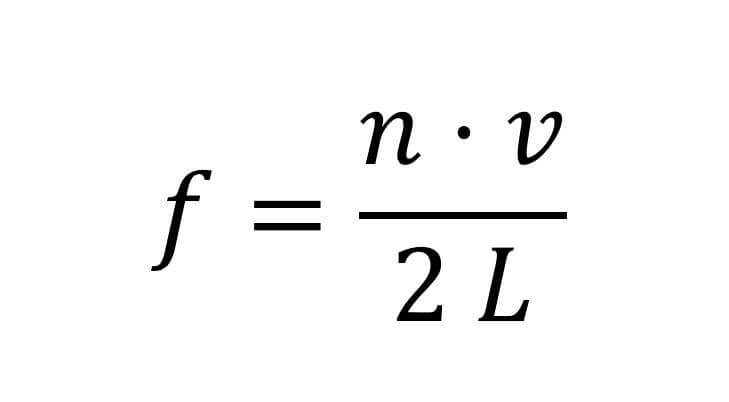
כאשר L הוא אורך המיתר, v היא מהירות הגל וn-  הוא מספר שלם שיכול לקבל את הערכים 1,2,3…

העובדה שהתדר f מתקבל ככפולות שלמות של גודל התלוי באורך המיתר אומר שלא ניתן ליצור כל תדר שנרצה. הסיבה לכך שקיבלנו תדרים מותרים נובעת מהאילוץ שהוספנו למיתר – תפסנו אותו משתי קצותיו ואילצנו את הגל בנקודת הקצה להתאפס. ננסה כעת לעבור למערכת קוונטית. נדמיין חלקיק בבור החסום בקיר גבוה מאוד (לצורך הדיוק קיר בגובה אין סופי ובעובי אינסופי). אם נזניח את אפקט המנהור הקטן (שאינו קיים בתנאי שהקיר אינסופי), אנחנו מונעים מהחלקיק להימצא בתוך הקיר ואחריו. במילים אחרות, ההסתברות של החלקיק להימצא באזור זה אפסי. מתמטית, התצפית הניסיונית שכרגע הסקנו מתורגמת לעבודה שפונקציית הגל של החלקיק מתאפסת בקצוות, ממש כמו מיתר קשור.

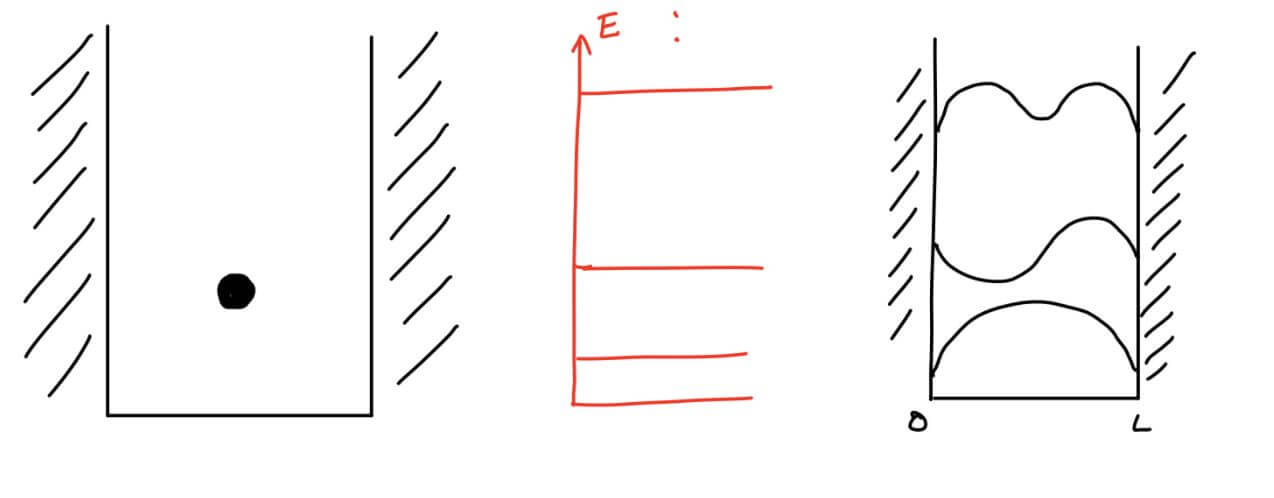
הבור העמוק הוא למעשה האנרגיה הפוטנציאלית שהחלקיק מרגיש בסביבתו. גם הכוח החשמלי שמושך את האלקטרון למרכז הגרעין יכול להיות מתואר כבור. הציור הבא מראה למשל את האנרגיה האפקטיבית שמרגיש האלקטרון בהשפעת פרוטון יחיד בגרעין (הציר האנכי) כפונקציה של המרחק (ציר האופקי).

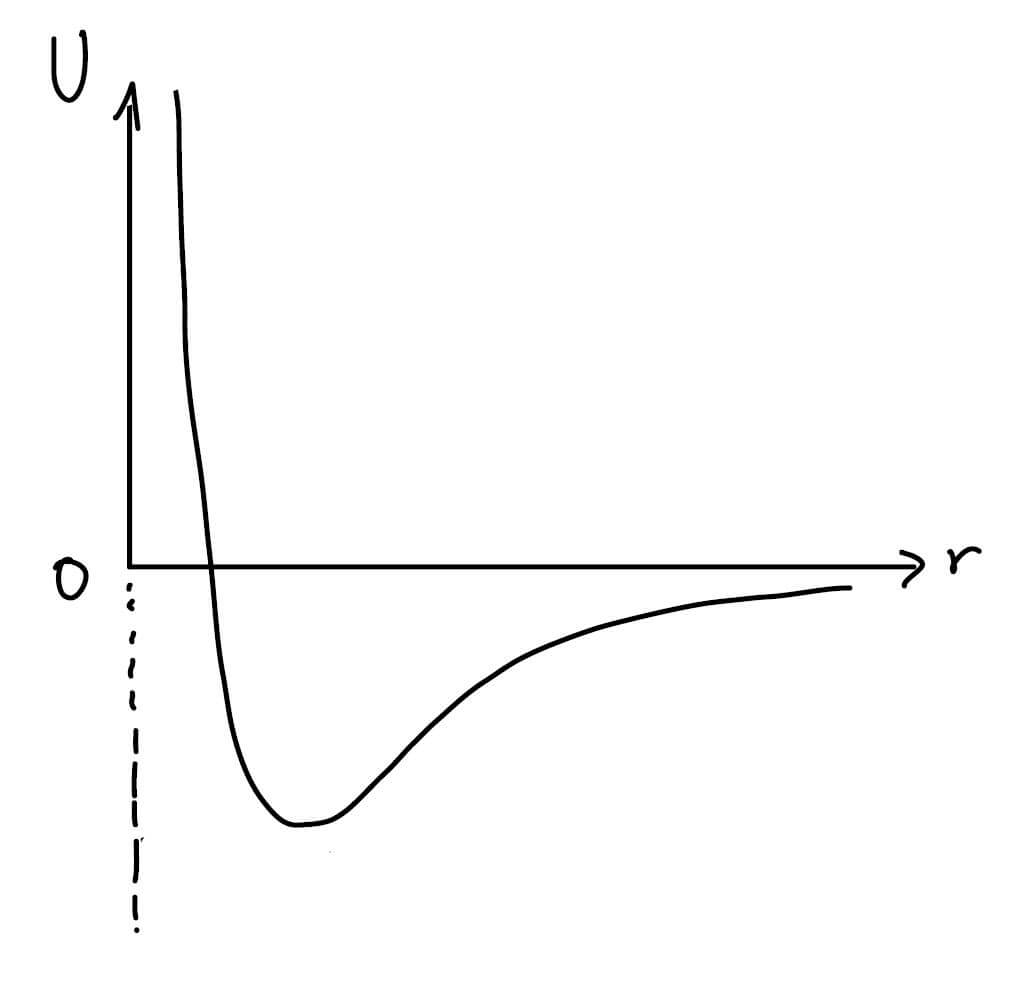
אם נחשוב על האלקטרון ככדור המתגלגל על משטח ששפתו מקובעת על ידי הגרף, האלקטרון ישאף ליפול לעמק. לתחתית העמק פיזיקאים קוראים רמת היסוד כי זו הנקודה שהאלקטרון ישאף להימצא באנרגיה הנמוכה ביותר. חשוב להזכיר שעיקרון האי וודאות אוסר על החלקיק להתמקם במדויק (אחרת האי וודאות בתנע היא אינסופית וברמת העיקרון קיימת הסתברות למצוא את חלקיק באנרגיה אינסופית גם כן, וזהו מצב פיזיקאלי אסור). לכן צריך להיזהר שבטיעון שהחלקיק נמצא אכן בתחתית ממש. יחד עם זאת, לאי וודאות תרומה משמעותית להתנהגות האנרגיה האפקטיבית ברדיוסים קטנים – בתחום זה האלקטרון מרוכז סביב הגרעין ולכן אי הוודאות במיקום קטנה מאוד. כתגובה נגדית, האי וודאות בתנע גדלה והאנרגיה האפקטיבית עולה לאינסוף. נציין שההתבדרות (העלייה המשמעותית לערכים גדולים) שמופיעה באנרגיה האפקטיבית עבור רדיוסים קטנים יכולה לנבוע גם מהתנע הזוויתי (בהנחה שאינו אפס). כעת נזכיר את העובדה שהאלקטרון “קשור”: העובדה שהחלקיק בתוך הבור אומרת שאין לו מספיק אנרגיה לברוח ממנו. קלאסית נזדקק להרים את החלקיק מעל הבור כדי להוציא אתו מהמצב הכלוא, אבל קוונטית כל עוד המחסום בגובה סופי ניתן להתמנהר, השאלה לאן? בסרטוט העליון נראה שעבור חלקיקים בתוך הבור (בעלי אנרגיה שלילית) הקיר ממשיך לנצח, לכן למנהור אין ממש משמעות. המסקנה המתמטית היא שפונקציית הגל ברדיוסים גדולים חייבת להתאפס כי ההסתברות למצוא את החלקיק שם אפסית. האם זה נשמע לכם מוכר? כמובן שכן, הדוגמא הזו דומה מאוד למיתר קשור או לחלקיק בבור שטוח. לפיכך נצפה שהאנרגיות המותרות לאלקטרון יהיו בדידות עד סף מסוים, הנקבע על ידי גובה הבור, המכתיב את האנרגיה הנדרשת שהאלקטרון יתנתק מהאטום.

המסקנה המתבקשת מדוגמאות אלו היא שהאופי הבדיד של מכניקת הקוונטים נובע מאילוץ הנקבע על ידי המערכת ואינו כלל טבע. הערה אחת מתבקשת היא לגבי הטיעון השגור ש”האור מגיע במנות”. שימו לב לכוונת המשורר – אין מדובר בכך שספקטרום האנרגיות של הפוטון (חלקיק האור) בדיד, חלקיק האור יכול לשאת כל אנרגיה שהיא, אלא מדובר בעובדה שבמקרים מסוימים ניתן להתייחס על אנרגיית האור כנישאת על גבי חלקיק יחיד ולא על גבי אובייקט רציף במרחב כמו גל. הערה אחרונה לגבי משוואת שרדינגר – מעבר לעובדה שהתיאור המתמטי של מכניקת הקוונטים לא רומז כלל על אופי בדיד כזה או אחר, הוא גם בכלל לא רומז על האופי ההסתברותי שלו. משוואת שרדינגר היא דטרמיניסטית לחלוטין, אין בה שום אלמנט אקראי. הרנדומליות היא חלק מההנחות של מכניקת הקוונטים הנובעת מתצפיות ניסיוניות.

בכל שבוע אקדיש כתבה לרעיון או למושג שגור בפיזיקה מודרנית. אם יש לכם הצעות או בקשות לפינה זו אתם מוזמנים לפנות אליי בכתובת המייל: [email protected]

לאלו המתעניינים, אני מצרף כנספח סקיצה לחישוב קצרצר מדוע התדר על מיתר קשור הוא דיסקרטי (בדיד). חישוב דומה גם נעשה עבור חלקיק בבור עם קירות אינסופיים. אציין שהחישוב אומנם נעשה עבור זמן אפס, אבל הוא נכון עבור כל רגע.

עוד בנושא באתר הידען:

• כמאה שנה לתורת שדות קוונטית – על התורה ששינתה את העולם
• האם כבידה פותרת את בעיית המדידה?