טלסקופ החלל האבל צילם קשר בהיר של גז שפגע בו סילון בלתי נראה מהחור השחור, המרוחק רק 15 שנות אור ממנו. החור השחור בוודאי נראה מזהיר לפני מיליארדי שנים כקוואזר (גוף מעין כוכבי), כשהגלקסיה הצעירה שלנו ניזונה מהרבה גז נופל. אבל אחרי כל הזמן הזה החור השחור פועל באופן ספורדי, ולא מוכן לנמנם

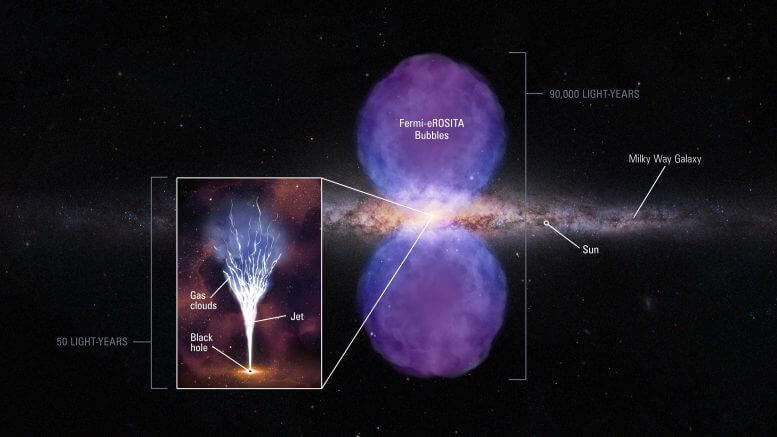
זה מראה מורכב של קרני רנטגן, גז מולקולרי וגז מיונן חם קרוב למרכז הגלקסיה. הצורות בצבע כתום הן גז מימן זוהר. אחת הצורות האלה, בקצה העליון של הסילון (ראו תמונה מבוארת בהמשך) מפורשת כענן מימן שפגע בו הסילון שנע החוצה. הסילון מפזר את הענן לקנוקנות שנעות לכיוון צפון. בהמשך למטה ליד החור השחור נמצאות תצפיות קרני רנטגן של גז מאוד מחומם בכחול וגז מולקולרי בירוק. הנתונים האלה הם עדות לכך שלחור השחור מתווספים מדי פעם כוכבים או ענני גז, והוא פולט חלק מהחומר המאוד חם לאורך ציר הסיבוב שלו. קרדיט: NASA, ESA, and Gerald Cecil (UNC-Chapel Hill); Image Processing: Joseph DePasquale (STScI)
יש סרטי מדע בדיוני שבהם מפלצת רדומה, כמו למשל גודזילה, מתעוררת פתאום ומתחילה להשתולל. פעם חשבו שבגלקסיית שביל החלב שלנו יש מפלצת רדומה בליבה, חור שחור ששוקל פי ארבעה מיליון ממסת השמש שלנו. אבל יש יותר ויותר הוכחות לכך שהחור השחור מתעורר מדי פעם וזולל כוכב או ענן גז אומללים שנופלים לתוכו. לאחר מכן נפלטות מסביבת החור השחור "קרני מוות" של קרינה וחלקיקים שנעים במהירות הקרובה למהירות האור. ההתפרצות המתועדת הגדולה ביותר הייתה לפני שני מיליון שנים. זה נראה בבירור בסילונים גדולים של פלסמה בצורת שעון חול, שמשתרעים הרבה מעל ומתחת למישור של הגלקסיה שלנו. גלי הלם דו-קוטביים מההתפרצות של החור השחור חיממו את הגז מחוץ למישור הגלקסיה והוא זוהר בקרני גאמה ורנטגן.
טלסקופ האבל מצא הוכחות נסיבתיות לכך שהחור השחור עדיין רוחש זמן רב אחרי ההתפרצות המוקדמת. המחקר של האסטרונומים של האבל מזכיר חפירה ארכיאולוגית בנסיון להציץ דרך הזיהום הבין כוכבי של יריעות עבות של אבק וגז שבין כדור הארץ ומרכז הגלקסיה, המרוחק מאיתנו 27,000 שנות אור. האבל צילם קשר בהיר של גז שפגע בו סילון בלתי נראה מהחור השחור, המרוחק רק 15 שנות אור ממנו. החור השחור בוודאי נראה מזהיר לפני מיליארדי שנים כקוואזר (גוף מעין כוכבי), כשהגלקסיה הצעירה שלנו ניזונה מהרבה גז נופל. אבל אחרי כל הזמן הזה החור השחור פועל באופן ספורדי, ולא מוכן לנמנם כל עוד יש חטיפים בסביבה
ב-2013 התקבלו הוכחות לסילון דרומי קצר ועבה ליד החור השחור מקרני רנטגן שהתגלו על ידי צ'נדרה וגלי רדיו שהתגלו על ידי טלסקופ ה-VLA ג'נסקי בסוקורו, ניו מכסיקו. נראה שגם הסילון הזה מתחיל כגז ליד החור השחור.
עוד בנושא באתר הידען:

4 תגובות
יבורך עצבריהו שהוכיח בדרך הניסוי שפאי זהה בכל מעגל בתחום שגיאת המדידה.
כפיים לעצבר!
והמתחיל במצווה, אומרים לו גמור. יבורך הידען, ומפעלו עוד ירשם בהיסטוריה של המדע.
מתמטיקה חדשה באה למדעים המדויקים ושמה העברי הוא כמתנות. היא סופרת עם מספרים, ומודדת עם מספרפרים.
הספירה מטפלת "בכמויות בדידות הכי קטנות" כמו ספרים, כסאות, עצים, מכוניות, פעימות לב, וכן הלאה.
עץ זה "כמות בדידה הכי קטנה" אין חצי עץ.
ספר זה "כמות בדידה הכי קטנה" אין שליש ספר ואין רבע ספר.
מטוס זה כמות בדידה הכי קטנה, וגם סלע , גם ענן, וגם מזלג.
פעולת הספירה של "כמויות בדידות הכי קטנות" פשוטה וידועה לכולם , אחת 1 , שתיים 2 , שלוש 3, ארבע 4 , וכן הלאה.
בחיים המעשיים צריכים לספור "הרבה דברים שהם כמויות בדידות הכי קטנות" ופעולת הספירה היא תמיד מדויקת.
אחרי הספירה באה פעולת המדידה, והיא תמיד לא מדויקת.
בפעולת המדידה מודדים כמויות רציפות ,כמו אורך ,משקל וזמן.
בכמות רציפה כבר יש חצי הכמות, שליש, רבע הכמות, חמישית הכמות,
ששית הכמות, שביעית הכמות, שמינית הכמות, וכך הלאה….. ללא סוף
המדידה של כמות רציפה היא פעולה מעשית ,הדורשת מכשיר מדידה.
בכדי למדוד אורך של עיפרון צריך להשתמש בסרגל.
תוצאת מדידה תמיד תהיה לא מדויקת, ואי אפשר להביע אותה עם מספר יחיד, אלא עם שני מספרים קרובים זה לזה. ככל ששני המספרים קרובים יותר זה לזה, כך המדידה מדויקת יותר.
הרישום של שני מספרים קרובים זה לזה, יכונה בשם מספרפר.
הרישום הזה (7)176 מ"מ הוא מספרפר ,המכיל שני מספרים הנובעים ממדידת אורך עיפרון.
המספר הקטן נמצא בצד שמאל של הסוגריים והוא 176 מ"מ,
המספר הגדול מתקבל מהחלפת הספרה האחרונה של המספר הקטן, בספרה הנמצאת בתוך הסוגריים.
המספרפר (7)176 מ"מ אומר שאורך העיפרון נמצא בין 176 ל 177 מ"מ
תוצאת מדידה תמיד תהיה עם מספרפר , ולא עם מספר יחיד. ככל ששני המספרים של המספרפר קרובים יותר זה לזה, כך המדידה מדויקת יותר.
תוצאה של מספר יחיד, קיימת רק בספירה של כמויות בדידות הכי קטנות.
ולסיכום :עם מספרים סופרים , ועם מספרפרים מודדים.
המדידה מחייבת להכיר את אמות המידה המוסכמות, של אורך ,של משקל , ושל זמן.
אמת המידה של אורך היא ס"מ, והיא מופיעה בעובי של 100 דפי A4
אמת המידה של משקל היא ק"ג, המופיעה בקוביית ברזל שאורך צלעה 5 ס"מ
אמת המידה של זמן היא "שנייה" והיא מופיעה בקירוב בין שתי פעימות לב.
בחברה מאורגנת אמות המידה של כמויות רציפות נשמרות במוזיאון מדע, והמבקרים יכולים לראות אותם, לחוש בהם, וכך לדעת אותם.
אחרי הביקור במוזיאון מבינים שלמספרים ולמספרפרים יש תפקיד פשוט שאמור לייצג שני סוגים של כמויות: כמויות בדידות , או כמויות רציפות.
לכן, השם המתאים לעוסקים במספרים ובמספרפרים הוא – כמתנים
בדמיון לחקלאים ושם המקצוע שלהם חקלאות,
ובדמיון לנגרים ושם המקצוע שלהם נגרות,
נקבל כמתנים , ושם המקצוע שלהם כמתנות.
הכמתנים הם אנשים מעשיים הסופרים כמויות בדידות הכי קטנות המופיעות במציאות, והם גם מודדים כמויות רציפות של אורך, משקל, וזמן בעזרת מכשירי מדידה.
את תוצאות המדידה הם מציגים עם מספרפרים.
מול הכמתנים קיימת קבוצת אנשים מיוחדת, העוסקת רק במספרים .
קבוצה זו בחרה עבור אנשיה את השם המוזר מתמטיקאים , כאשר שם המקצוע שלהם מתמטיקה.
מי הם אלה המכנים את עצמם בשם המוזר מתמטיקאים ?
קשה מאוד לענות על שאלה זו, אבל אפשר להגיד כי מדובר בחבר בני אדם האוהבים לחקור מספרים סתם כך ,כי זה מעניין אותם.
המתמטיקאים מתעסקים עם המספרים כאילו יש בהם סודות פלאיים עמוקים ונסתרים, ולכן צריך לחקור אותם.
המתמטיקאים גם ממציאים שאלות מוזרות – שאין להם קשר לחיים המעשיים ( כמו האם יש סוף למספרים ראשוניים ), ואז הם מנסים לענות בעצמם על השאלות שהם עצמם שאלו.
והיות שהם מנסים לענות בעצמם על השאלות שהם שאלו, הם גם חייבים להוכיח לעצמם, כי התשובה שהם נתנו לעצמם היא נכונה.
המתמטיקאים אוהבים את הדיוק המושלם, והם מאוד מעריכים את פעולת הספירה המדויקת אחת, שתיים, שלוש, ארבע, ……וכן הלאה ללא סוף.
המתמטיקאים פועלים עם הגדרות מדויקות, והיגיון מושלם, וכך הם חוקרים את תעלומות המספרים , ומנסים לפצח את סודם.
ואילו הכמתנים ממש הפוכים מהמתמטיקאים.
הכמתנים חושבים שאין שום סוד פלאי במספרים, ואין צורך לבזבז זמן ולחקור אותם. הכמתנים חושבים שלמספרים יש תפקיד פשוט מאוד , והוא לייצג כמויות. הכמתנים גם יודעים שהמספרים מייצגים ממש במדויק כמויות בדידות הכי קטנות, אבל ייצוג כמות רציפה אינו אפשרי עם מספר, והוא נזקק למספרפר.
והמתמטיקאים ימשיכו להיות הפוכים מהכמתנים.
אומנם הם סופרים "כמויות בדידות הכי קטנות" אבל הם לעולם לא ישתמשו במכשירי מדידה של כמויות רציפות, וכמובן הם לא ישתמשו במספרפר. המתמטיקאים פוסלים מראש את השימוש במכשירי מדידה , מכיוון ששימוש זה בהכרח אינו מדויק.
פסילת מכשירי המדידה של הכמתנים, חייבה את המתמטיקאים
להציג דרך משלהם לטפל בכמויות רציפות.
ואכן הם הציגו דרך מיוחדת ומפתיעה לטפל בכמויות אורך רציפות המופיעות בתחום הגיאומטרי, בלי להשתמש כלל במכשיר למדידת אורך.
למרבה הפלא ,הדרך של המתמטיקאים הצליחה.
המתמטיקאים השתמשו במשפט פיתגורס, והם הצליחו "למדוד" את אורך האלכסון של ריבוע , שאורך צלעו 1 , זאת לא הייתה מדידה עם מכשיר מדידה, אלא עם שיטה מתמטית מתוחכמת הפועלת על קטעי קו ישר והיא הפיקה תוצאה של מספר שאין לו סוף הנרשם כך …1.41421
את התוצאה של …1.41421 יש להבין כך:
אם אורך צלע הריבוע מיוצג על ידי 1 , אז אורך אלכסון הריבוע יהיה מיוצג על ידי…1.41421
יש להדגיש כי אם הכמתנים היו מודדים את אורך האלכסון של ריבוע – שאורך צלעו 1 מטר, התוצאה בקושי הייתה 1.414 מטר, כאשר על פי שיטת המתמטיקאים התוצאה הרבה יותר מדויקת והיא …1.41421 מטר.
בעקבות ההצלחה בתחום הגיאומטרי, זכו המתמטיקאים להערכה עצומה, והם הפכו להיות לאנשים היחידים המוסמכים לטפל בגיאומטריה האוקלידית, שנחשבה תמיד למדע אידיאלי מדויק ומושלם.
המתמטיקה הפכה להיות מלכת המדעים המדויקים, ושפת המתמטיקה הפכה להיות שפת המדע על כל גווניו.
מעמד המתמטיקה הפך להיות כזה חשוב בשנים האחרונות, עד שמחקר שאינו משתמש בשפת המתמטיקה, נחשב מחקר לא רציני.
אבל כמו בטרגדיה יוונית, הכל התהפך פתאום.
השיטה המתמטית המתוחכמת שהגיעה למספר …1.41421 נתגלתה על ידי עצבר כמדידה בדמיון בעזרת ריבועים זעירים (ריבו"זים), ולכן אפשר לייצג את אורך אלכסון הריבוע עם המספרפר (2)1.41421
כמובן שהמתמטיקאים לא הסכימו לקבל את הרעיון שהשיטה המתמטית שלהם דומה למדידה בעלת תוצאה לא מדויקת של מספרפר , ולכן הם
לא הסכימו להשתמש במספרפר (2)1.41421
הכישלון הראשון של המתמטיקה בתחום הגיאומטרי הוא ההתעלמות
מזיהוי פעילות המתמטיקה בתחום הגיאומטרי, כמדידה הנערכת בדמיון, כאשר אמת המידה היא ריבוע זעיר. (ריבו"ז)
אחרי הכישלון הראשון הופיע כישלון מחפיר ממש.
הכישלון המחפיר של המתמטיקאים בתחום הגיאומטרי התרחש, כאשר הם קבעו "כי קטע זעיר של קו עגול שאורכו שואף לאפס" נראה בדיוק כמו "קטע זעיר של קו ישר שאורכו שואף לאפס".
הכישלון המחפיר של המתמטיקאים היה בגדר של אסון, שעיכב את התפתחות הגיאומטריה במשך 2000 שנים. המתמטיקאים כלל לא הרגישו באסון שהם המיטו על התפתחות הגיאומטריה, והם היו בטוחים שדווקא הם הביאו פריחה לגיאומטריה.
אבל הכישלון המחפיר של המתמטיקאים הקפיא את הגיאומטריה,
והיא נשארה כמו שהייתה לפני 2000 שנים.
רק בשנת 2017 – בעקבות מדידה מדויקת שהופיעה בניסוי ההיקפן , נפתח השער לתגליות שהמתינו בסבלנות 2000 שנים.
בשנה זו נתגלתה גיאומטריה חדשה, והיא הגיאומטריה של קווים עגולים סגורים. אחריה נתגלתה הגיאומטריה של קווים משולבים.
הגיאומטריות החדשות הן של הכמתנים העוסקים גם במדידות.
למתמטיקה נשארה רק הגיאומטריה של הקו הישר, המבוססת על משפט פיתגורס, ויש לה את האפשרות להשתמש במספרפרים.
מעתה יש 3 סוגים של גיאומטריה.
של הקו הישר, של קווים עגולים סגורים, ושל קווים משולבים.
מעתה הגיאומטריה היא מלכת המדעים המדויקים , ולמתמטיקה נשאר
רק לספור , אחת, שתיים, שלוש, ארבע,,,,,וכן הלאה ללא סוף
את פעולת הספירה המהירה לקחו על עצמם המחשבים, את הפעילות בתחום הגיאומטרי לקחו על עצמם הכמתנים, והמתמטיקאים ימשיכו
לחקור את המספרים בתקווה למצוא משהו מעניין.
פירוט הסיפור הזה נמצא ב 5 קבצים ובסרטון של ניסוי ההיקפן.
א.עצבר
תודה רבה לידען שהסכים לתת במה למידע שיועיל לכל תלמיד מתמטיקה בעולם.
המתמטיקה היא מדע תיאורטי הבנוי ממלים ומספרים, ודרגת האמינות של מדע כזה היא נמוכה מאוד.
ידיעות כזב קיימות בכל חברה אנושית, וגם בקרב החברה האנושית העוסקת במדע תיאורטי ובמדע מעשי.
מדע תיאורטי בנוי ממלים שהם תיאוריה , ואין בו מעשים.
מדע מעשי בנוי ממלים שהם תיאוריה, אבל יש בו מעשים.
הפיזיקאים עוסקים במדע מעשי והם מצאו את הדרך "לפסול ידיעות כזב"
הפיזיקאים מעמידים תמיד את הרעיונות שלהם למבחן הניסוי המעשי. הנערך במציאות הפיזיקלית הטבעית.
ניסוי מעשי חדשני יכול לפסול תיאוריה פיזיקלית שהייתה מקובלת במשך שנים רבות, ובמקומה תבוא ללא היסוס תיאוריה חדשה.
לכן לא פלא הוא שהפיזיקה כמדע מעשי משתנה ללא הרף, ובעקבות השינויים היא משתפרת בהבנת המציאות, ומגיעה להישגים מעשיים מופלאים , הנמצאים כיום על גבול המדע הבדיוני.
לעומת זאת המתמטיקה היא מדע תיאורטי הבנוי ממלים ומספרים, ואין בו מעשים. המתמטיקאים לא רגילים להעמיד את הרעיונות שלהם למבחן הניסוי המעשי , והם מסתפקים במבחן ההיגיון של עצמם.
המתמטיקאים הלכו מההתחלה בדרך התבונה הטהורה וההיגיון הצרוף, מכיוון שהם האמינו שהתבונה וההיגיון הצרוף , יובילו אותם אל האמת.
אבל תבונה והיגיון צרוף הם רק מלים, והן בונות רק תיאוריה.
חובה להדגיש כי המתמטיקאים קבעו בעצמם מהו ההיגיון הצרוף ומהי התבונה הטהורה, ולכן הם הציגו את המתמטיקה כמבנה רעיוני הגיוני שאין בו טעויות, ושלא ייתכן שיהיו בו טעויות.
העיסוק המתמטי מעולם לא פיתח מנגנון ביקורת טבעי שקיים במציאות מכוח עצמו, והמתמטיקה בדקה את עצמה, אך ורק בכוח עצמה.
לכן, בהכרח נוצרה כאן אפשרות , שידיעות כזב מתמטיות יקננו בתוך המתמטיקה במשך מאות שנים, ולא תהיה כל דרך לסלקן.
ומדוע לא תהיה אפשרות לסלקן ? מכיוון שהמתמטיקה כבר קבעה מראש "שהיא עצמה מבנה רעיוני שאין בו טעויות, ולא ייתכן שיהיו בו טעויות"
כך נוצרו כל התנאים, שידיעות כזב יקננו בתוך המתמטיקה אולי לנצח.
והמסקנה הבלתי נמנעת היא זו:
המתמטיקה היא מדע תיאורטי הבנוי ממלים ומספרים, ודרגת האמינות של מדע כזה נמוכה מאוד.
רשימה קצרה של ידיעות כזב המקננות בתוך המתמטיקה הפועלת בתחום הגיאומטרי.
קיימת ידיעת כזב מתמטית עוד מתקופת ארכימדס, הקובעת כי מספר יחיד שערכו כ 3.14 , הוא שמאפשר את המעבר בין קוטרו של כל מעגל ( קטן או גדול) אל אורך ההיקף שלו.
את ידיעת הכזב הזו אפשר לסלק מהמתמטיקה, רק בדרכם של הפיזיקאים, כלומר בדרך של ניסוי מעשי ממשי.
דרך כזו נפסלת מיד על ידי המתמטיקאים, כיוון שהם קבעו שרק בדרך התבונה וההיגיון אפשר לדבר אתם.
אבל בדרך התבונה וההיגיון, המתמטיקאים כבר קבעו שאין טעויות במתמטיקה, ולכן אין טעם ואין צורך להציע ניסוי מעשי, שאמור לגלות שיש ידיעת כזב, בתוך המתמטיקה.
לכן , המתמטיקה עצמה, מונעת כל אפשרות לסלק מתוכה ידיעת כזב.
המתמטיקה גם פעלה בתחום הגיאומטרי של קווים עקומים בעזרת החשבון של ניוטון ולייבניץ, וגם פעילות זו מכילה ידיעות כזב.
התחום של המתמטיקה שאין בו ידיעות כזב, הוא התחום שבו סופרים אחת, שתיים, שלוש, וכן הלאה.
זה בדיוק התחום שבו פועלים המחשבים המסוגלים לספור מהר.
א.עצבר
ומה עם החור השחור של לימודי המתמטיקה ?
שיר זה מתאר את המתמטיקה הבלתי הגיונית הפועלת בתחום הגיאומטרי זה כבר 2000 שנים, ומלמדים אותה בבתי הספר.
שנאת מתמטיקה היא תגובה טבעית ללימוד כזה, ולא פלא שהיא מתפתחת לחרדת מתמטיקה הדורשת טיפול פסיכולוגי.
תקוותי היא שהממונים על לימודי המתמטיקה במשרד החינוך יבטלו את המתמטיקה הבלתי הגיונית הפועלת בתחום הגיאומטרי, ויפתח השער ללימודי הכמתנות המתאימים לטבע האדם.
שיר שמח ( חדו"א ) ובעצם הוא שיר עצוב.
מי כאן סופר ומי מונה
בא בריצה דקארט רנה
אין קו יותר ואין צורה
זו ממש צרה צרורה
אני חושב אני קיים
והאמת טבעה בים.
אוי לי ווי לי מה קרה לי
הבלגן ממש טוטאלי
איני – פיני – טסי – מלי
דיפרנציאלי ואינטגרלי
אין מפלט ואין מנוס
סביב סוגר קלקולוס
הגבול ברח קפצה נגזרת
לא הבנתי, מה זאת אומרת
טורי אינסוף על הסולם
התאספו כאן ,כל כולם
נדחקים בשצף קצף
מחפשים הם את הרצף
ומשיקים כה עדינים
מחפשים מעגלים
תרים אחרי נתיב עומקה
של נקודת ההשקה
והפונקציה זזה ומתפתלת
ממתינה לאנליזה קצת אחרת.
ארכימדס נתן כאן טון
ואחריו גם בא ניוטון
ומי באופק שם מציץ
אולי אולי זה גם לייבניץ
שביל הסטוריה כבר נפרס
הנה צועד פיתגורס
אוי לי ווי לי מה קרה לי
הבלגן ממש טוטאלי
איני – פיני – טסי – מלי
דיפרנציאלי ואינטגרלי
אין מפלט ואין מנוס
סביב סוגר קלקולוס
א.עצבר