חוקרים ישראלים ואירופאים הצליחו להוכיח השערה ותיקה בגיאומטריה קומבינטורית
החוקר ד"ר נתן רובין מהמחלקה למדעי המחשב באוניברסיטת בן-גוריון בנגב הוכיח תוך שיתוף פעולה עם פרופ' יאנוש פאך, מהמרכז הטכנולוגי-פדרלי של שוויץ ופרופ' גאבור טארדוש ממרכז אלפרד רני למתמטיקה בבודפשט, השערה ותיקה משנת 1996 בגיאומטריה קומבינטורית.
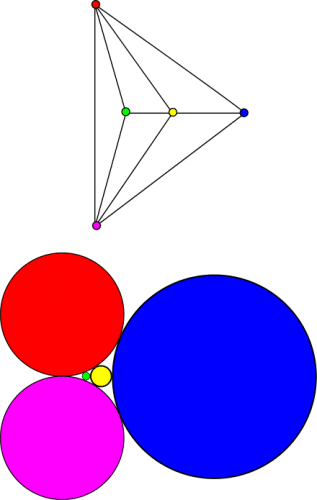
רקע למחקר: משפט האריזה של מעגלים המפורסם של Koebe משנת 1936 מספק התאמה יסודית בין מפות מישוריות לאריזות של דיסקים במישור, כלומר, סידורים של מטבעות ללא חפיפה על שולחן שטוח (ראו תמונה).
מצד שני, תיאורית "למת החיתוכים" משנת 1982 מקשרת בין צפיפות הרשת למספר חפיפות בציור המישורי שלה, כלומר "ככל שרשת דרכים צפופה יותר, כך גדל מספר המחלפים הנדרשים".
התוצאות לעיל הינן מרכזיות בגיאומטריה קומבינטורית ומצאו שימושים נרחבים בגיאומטריה חישובית. זהו תחום קרוב למדעי המחשב שעוסק בפתרון בעיות בעלות אופי גיאומטרי, אשר צצות במגוון תחומים כגון תכנון תנועה רובוטית, ציור מפות, ביולוגיה חישובית וכדומה.
במחקר הנוכחי, החוקרים הוכיחו את השערת ריכטר-תומסן משנת 1996 על ידי הכללה שאפתנית שלה. החוקרים הראו את התופעה המקבילה ללמת החיתוכים עבור "רשתות" של עקומים מישוריים, המתארות השקות בין עקומים פשוטים במישור. תוצאה זו מצמצמת את הפער בין שני עולמות מתמטיים (עקומים פשוטים ומפות מישוריות), וצפויות לה שימושים נרחבים בגיאומטריה חישובית, בין היתר בתחום של ציור מפות. מבחינה מתמטית, מדובר באבחנה מפתיעה מכיוון שעד היום רוב התוצאות הכמותיות בתחום נגעו רק לעקומים אלגבריים מדרגה נמוכה, כדוגמת ישרים ומעגלים. לעומת זאת, עקומים פשוטים כלליים תמיד היוו אתגר יוצא דופן לניתוח כמותי עקב התנהגותם הבלתי נשלטת (כל שני עקומים יכולים להיפגש מספר שרירותי של פעמים).

2 תגובות
נראה שקהל היעד של הפרסום (שהועתק ככתבו וכלשונו מאתר אונ. ב"ג) הוא מתמטיקאים מקצועיים ולא הציבור הרחב.
כמעט ואין מידע רלוונטי בכתבה.