יוהאן קרל פרידריך גאוס תיקן בגיל שבע טעויות חישוב שכר שערך אביו. בהמשך, בתוך עשר שנים הוא כתב שבעים מאמרים מדעיים קריטיים. היום אין כמעט מדענים שמדביקים אותו
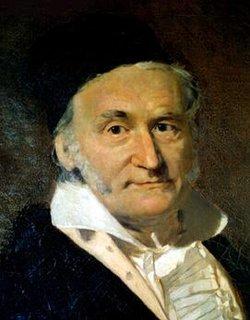
תקופות המבחנים של אשתי במהלך לימודיה היו כר פורה לעולמות חדשים איתם באתי במגע בפעם הראשונה. עובדת היותי מנמנם תוך כדי הסברים על הדרך בה רואה הפסיכולוגיה את פעילותו של המוח האנושי לא מנעה ממנה להמשיך ולפרט באוזני את תוצאות מחקריו של פרויד. דא עקא, ניעורתי לחיים כאשר החלה עומדת על טיב מוחם של גאונים, ופרט אחד ממחקרים לא מעטים שבה את תשומת ליבי, המדובר במונח "פיתולי מוח", ובלשון פנים-טריטוריאלית – הקיפולים הלבנים-אפורים הנראים כאילו נוצרו על ידי אמן אוריגאמי כושל. הטענה המעניינת העלתה השערה מבוססת כי מספר הפיתולים הוא הגורם העיקרי לגאונותו של אדם. מוחו של המתמטיקאי הגרמני עליו בחרתי לדבר הפעם משומר בצנצנת עד היום ונמצא כי הוא בעל מספר הפיתולים הרב ביותר הידוע בספרות המדעית. אז כן, הייתי יכול לתת את דעתי על המסקנה המתבקשת והברורה מדברים אלו, אלמלא אני מביט כרגע בתמונתו של גרמני אחר אשר שיבתו מתבדרת פרא מעל ראשו והוא, איך נאמר זאת – משתייך לזרעה של אומה שבה גם אני חבר בה דרך קבע. אך כעת עסקינן בזה המכונה על פי רוב – "נסיך המתמטיקאים" וסיפורו המופלא בכל שנות חייו – גאוס.
יוהאן קרל פרידריך גאוס (Johann Carl Friedrich Gauss) נולד בגרמניה בשנת 1777 וכבר בילדותו ניכר בו כי היה שונה מכל שאר הסובבים אותו. סיפורים רבים נקשרו בילד הפלא על שלל יכולותיו המתמטיות שהחלו, כך לפי דבריו, עוד בטרם ידע לדבר. היטיב לספר על כך כותב הביוגרפיות אריק טמפל בל בספרו המפורסם Men of Mathmatics. נטען כי כבר בגיל 3 ניכרה בו הגאונות המתמטית כאשר אביו עסק בהכנת גיליון שכר למספר עובדים ולאחר זמן רב של חישובים גילה גאוס הקטן טעות חישוב בן רגע. דבר נוסף הוא יכולתו המדהימה ללמוד שפות זרות, נאמר כי כבר בגיל 4 ידע גאוס 3 שפות על בוריין. סיפור אחר, ככה"נ הידוע ביותר, התרחש בין כותלי בית הספר בו למד בגיל 7. התלמידים בכיתה עוררו המולה וקיבלו כעונש לחשב את סכום המספרים מ-1 ועד 100. באותה העת חישוב שכזה היה אורך דקות ארוכות לאדם מבוגר ממוצע, ואילו גאוס הצליח לפתור זאת לאחר מספר שניות ומבלי לשים לב "המציא" ענף חדש במתמטיקה. חלק מדברים אלו נראים, איך נאמר זאת, לא אנושיים ונראה כי אכן חלק מהם בדיות, אך לאחר קריאת הביוגרפיה הבאה גם בספקן הגדול מכולם יתעוררו אי אלו תהיות האם אכן מדובר רק בסיפורים או שמא אמת הם.
גאוס החל ללמוד בגיל 11 בגימנסיון ובגיל 15 כבר זכה למלגת לימודים באקדמיה מטעם דוכס מקומי שם גילה באופן עצמאי את "חוק בודה" (בנוגע לתנועת כוכבים), התיאוריה הבינומית, הממוצע האריתמטי-גיאומטרי ותיאוריות חשובות בנוגע למספרים ראשוניים, אלו המספרים המתחלקים רק בעצמם ובספרה 1. בגיל 18 התחיל את דרכו באוניברסיטת גטינגן שם הכיר את חברו היחיד פרקש בולייאי, שבנו , ממייסדי הגיאומטריה הלא-אוקלידית עתיד להיות גם הוא מגדולי המתמטיקאים בכל הזמנים.
גאוס סיים את לימודיו כאשר הוא משאיר מאחוריו את אחד ההישגים הכבירים מאז ימי המתמטיקה היוונית שעסק בבניית צורות גיאומטריות מסובכות באמצעות מחוגה. בהמשך דרכו כאשר היה רק בן 24 חיבר ספר מהפכני אודות תיאוריית המספרים ובאותה שנה גם טעם מעולם האסטרונומיה כאשר הוא משלב כוחות עם דמות מפורסמת בעולם זה בשם זאך (Zach) במחקרים הנוגעים למסלולי כוכבים. יכולתו של גאוס באה לידי ביטוי גם כאן כאשר ידע לתאר את המסלולים באמצעות התיאוריה החדשה אותה פיתח הידועה בשם "שיטת הריבועים הפחותים" (תיאוריה המרכזית המהווה את הבסיס ללימודי הסתברות וסטטיסטיקה על ענפיהן).
בגיל 32 התמנה גאוס לראש מצפה הכוכבים באוניברסיטה בה למד ושם כתב את ספרו עב-הכרס השני שעסק בגופים שמימיים (כוכבים ותנועתם) בו הוא תרם רבות לפיתוח המשוואות הדיפרנציאליות, מסלולים אליפטיים של כוכבים ותיאור כללי של מציאת מיקומו של כוכב על פי מסלולו. גאוס המשיך לאורך זמן רב בתפקיד זה אך בו בעת ערך מחקרים רבים בנושאים מגוונים כגון סדרות של מספרים, הפונקציה ההיפר-גיאומטרית (הקשורה גם היא לתורת ההסתברות), אינטגרציה (שעוסקת במציאת שטחים), הסתברות כללית, משוואות דיפרנציאליות חלקיות (מה שכולנו למדנו בתיכון כ-"נגזרת" אך עם עוד כמה משתנים) והתחום אותו אהב יותר מכל – חקר כדור הארץ והכוחות הפועלים בו, בעיקר בנושא כוח הכבידה. ב-1818 התבקש לערוך מחקר רחב היקף בנושא אחרון זה תוך שהוא מקבץ כמויות אדירות של נתונים במהלך היום ועורך את כל החישובים המסובכים בראשו במהירות הבזק (להזכירכם לא היה אז מחשבון או טבלאות אקסל). במהלך מחקר זה המציא את המכשיר הידוע כ-"הליוטרופ" בו משתמשים לצורך מדידת קרקע באמצעות שימוש באור השמש. מחקר זה ויתר תחומי העניין של גאוס הניבו יותר מ-70! מאמרים מדעיים קריטיים תוך 10 שנים בלבד. רק לצורך המחשה, עבודת דוקטורט כיום אורכת בממוצע 3-4 שנים, ואילו גאוס כתב 70 עבודות ברמה דומה (פחות או יותר) במשך הזמן שלוקח לאדם רגיל (וחכם בד"כ) לכתוב 3 מאותו הסוג.
במהלך שנות ה-80 של אותה מאה, בעיקר בשנת 1816 כשהיה בן 39 החל לחקור את התורה הידועה כיום כגיאומטריה לא-אוקלידית תוך שהוא מצליח להוכיח את חוסר ההקבלה של קווים מקבילים. תיאוריה זו נודעה בעולם המתמטיקה עוד בימי היוונים ונתחברה על ידי אוקלידס. בכדי לרשום את ספרו "האלמנטים" אוקלידס הניח הנחות כאקסיומות כאשר החמישית בהן הייתה הטענה (בתיאור פשוט) כי קווים מקבילים לעולם לא יפגשו. מתוך הסבר זה ניתן לחשוב כי מדובר ב-"עוד טענה מתמטית", אך פני הדברים הם הפוכים לחלוטין ומדובר אם כן באחד היסודות עליהם הונחה המתמטיקה לדורותיה. גם גאוס עצמו ידע זאת ולמרות חליפת מכתבים עם מתמטיקאים עמיתים סרב לפרסם תיאוריה כה מהפכנית אשר במידה ונמצאה שגויה – הייתה מעמידה את "נסיך המתמטיקאים" באור מגוחך למרות הישגיו. כפי שנאמר בתחילת הכתבה, את התיאוריה המהפכנית הזאת יבצעו וישכללו לאחר מכן תלמידו הגאון של גאוס – ברנרד רימן (Riemann), יאנוש בולייאי (Bolyai, בנו של פרקש בולייאי) ומתמטיקאי רוסי בשם לובצ'בסקי (Lobachevsky). משעשעים מאוד (וקצת יהירים) היו דבריו של גאוס למתמטיקאי עמית כאשר שמע על מחקרו של לובצ'בסקי: "הקדמתי אותו ב-54 שנה" , כלומר שכביכול הגה את רעיון הגיאומטריה הלא-אוקלידית כבר בגיל 15.
גאוס מצא עניין רב בתחום הגיאומטריה הדיפרנציאלית ושילוב ידיים עם הפיסיקאי הגדול וובר (Weber) הניב מספר רב של ספרים ומאמרים על אודות כדור הארץ והכוחות הקיימים בו, ובעיקר זה המגנטי. תוך שהם מתבססים על כתביהם של ענקי המתמטיקה פואסון (Poisson), דיריכלה (Dirichlet) ולפלס (Laplace), פילסה עצמה תגלית בסדר גודל עולמי (תרתי-משמע) כאשר השניים הצליחו להוכיח שעל פני כדור הארץ יכולים להיות רק שני קטבים מגנטיים וגאוס אף ציין באופן מדויק את מיקומו של השדה המגנטי מעל הקוטב הדרומי. עבודת הצוות הזאת הביאה בעקבותיה גם את המצאת ה-"האי-מייל" הראשון, מעין מכשיר פרימיטיבי לשליחת הודעות למרחק של כקילומטר וחצי. בשנת 1837 וובר נאלץ לעזוב את גטינגן כתוצאה מסקנדל פוליטי בו היה מעורב ודבר זה גרם להאטה משמעותית במחקריו ומאמציו של גאוס, אך הדבר אשר בו המשיך ללא לאות הוא התכתבות ענפה עם מתמטיקאים עמיתים בה תמיד זכר לעקוץ אותם כי כל תוצאות מחקריהם רבות השנים גילה הוא בעצמו זמן רב לפני כן, ולא חש צורך להציג אותן בפומבי ; אם היה חי בימינו הרי היה יכול לתמצת זאת לשתי מילים – "נו, באמת…". אך למרות זאת, מפתיע לגלות כי מבין כל האחרים, גאוס דווקא כן העריך מתמטיקאי יהודי עילוי בשם פרדיננד אייזנשטיין (Eisenstein) שגם הוא, כמו אווריסט גלואה (Evariste Galois), נפטר לפני הגיעו לגיל 30 ואת סיפורו נביא בפעם אחרת.
בשנותיו האחרונות של גאוס שימש כפרופסור מלווה של שני דוקטורנטים למתמטיקה, גם הם מטבע הדברים כלולים בפנתיאון של הגדולים ביותר, ושמם מוריס קנטור (Cantor) ו-דדקינד ((Dedekind. השניים רשמו תיאור מרתק אודות התנהלותו של גאוס כאשר היה נותן דרור למחשבותיו – "בדרך כלל הוא היה יושב בניחותא ומסתכל למטה בעודו משלב ידיים. הוא היה מדבר בחופשיות, בבהירות ובפשטות, אבל כשרצה להסביר לנו תיאוריה חדשה הוא היה מרים את ראשו ובאמצעות עיניו הכחולות היפות היה נועץ מבט חודרני בזה שישב לצידו לאורך כל השיחה. במידה והיו הוכחות מתמטיות לדבריו היה קם מכיסאו ומתחיל לשרבט על הלוח נוסחאות בכתב יד מדהים. כאשר היה נדרש לדוגמאות מספריות, עליהן נתן דגש מיוחד, היה כותב אותן על פיסות נייר קטנות".
בשנת 1855 בריאותו החלה להתדרדר לאט עד שנפטר בשנתו בבוקרו של יום חורפי.

41 תגובות
בכתבה נאמר "ואילו גאוס הצליח לפתור זאת לאחר מספר שניות ומבלי לשים לב "המציא" ענף חדש במתמטיקה". גם בכתבות רבות נאמר שגאוס, בלי לשים לב, "המציא" את השיטה לסיכום טור אריתמטי.
אם נעיין בבעלי התוספות במסכת מנחות דף ק"ו עמוד א', בדיבור המתחיל "שהם אלף שמונה מאות ושלושים", נראה, מפורט, את השיטה שכביכול "המציא" גאוס. בעלי התוספות חיו במאה השתיים עשרה ובמאה השלוש עשרה לספירה. כלומר, השיטה הזאת קיימת, שחור על גבי לבן, לפחות חמש מאות שנים לפני גאוס
איך קוראים לי?
יש בכתבה שגיאת הבנה של היחסים בין התורות הגאומטריות.
אם נתון ישר ונתונה נקודה נפרדת שאינה כלולה בישר, האם יש מקביל לישר, שעובר דרכה?
תתכן רק אחת משלוש אפשרויות:
1. יש לישר מקביל(ים) שעובר(ים) דרך הנקודה הנתונה.
2. אין לישר שום מקביל שעובר דרך הנקודה הנתונה.
3. הנתונים אינם מספיקים לענות על השאלה.
לפי כללי הגאומטריה שפותחו עד לדיון בשאלה זו, אין דרך להוכיח מי משלושת התשובות נכונה.
הגאומטריה האויקלידית בחרה בתשובה מספר 1 כנקודת מוצא. לזאת קוראים: אקסיומה. הנחה שרירותית שלא הוצגה לה הוכחה. (ובהמשך: יש רק ישר אחד שמקביל לנקודה)
יש עוד גיאומטריה לא אויקלידית שבחרה את תשובה 1 כאקסיומה (ובהמשך: יש אלומה של אין סוף ישרים שעוברים דרך הנקודה הנתונה וכולם מקבילים לישר הנתון)
ויש גיאומטריה לא-אויקלידת נוספת שבחרה בתשובה 2 בתור אקסיומה.
ומה לגבי תשובה 3? ככל הידוע לי – זה כיוון שלא נחקר.
(לפי הנאמר בכתבה – ניכר שאין כאן הבנה של הנושא)
כתבה מעולה, מעניינת ומרתקת! אפילו אותי שאני רק בת 13, הצלחת לרתק. תודה רבה לירן.
אני כולה בכיתה ד בת 9 וחצי למדתי דברים שלומדים רק בתיכון חחחחחחחחחחחחחחחחח
למדתי הרבה מ-גאוס אלוף החשבון
קראתי בויקיפדיה שהסיפור של העונש שממנו יצאה הסידרה החשבונית הוא פיקציה… אבל אחלה סיפור בכל מקרה.
וכמובן מאמר מעניין מאד!
יפה אבל אני כולה בן 9 חח אני רוצה שיום של הצורות איך אומרים נגיד צורה שיש לה 7 צלעות 8 ו9
קודם כל אפתח ואציין שאין ספק שהנושא בו בחרת לעסוק הוא מעניין לכשעצמו וכמו שנאמר בתגובות לפניי, תמיד נחמד לדעת מי האנשים שעומדים מאחורי המשפטים והנוסחאות אותן שיננו בתיכון. אינני מתמטיקאית כי אם בן אדם פשוט עם חיבה לנושא, ועם זאת הביקורת שהופנתה מצד גדי "הוציאה לי את המילים מהפה" . אני סבורה כי ניתן לכתוב מאמר במתמטיקה ולהסביר בצורה נהירה גם לאדם ללא זיקה כלל לנושא אם לוקחים בחשבון שני פקטורים משמעותיים. האחד הוא שעם קצת יצירתיות אפשר לפשט תחומים מסובכים לדוגמאות פשוטות להבנה והשני הוא לתת קצת יותר קרדיט לקורא. אם אתה יוצא מנקודת הנחה שלצרף נוסחה על מנת להבהיר טענה במאמר שעוסק במתמטיקה (כמה אבסורדי) זה גדול על הקורא אתה קצת מזלזל באינטליגנציה שלו, דבר שאני בטוחה שלא התכוונת לעשות. אם אני מסוגלת להסביר לאחותי שקוראת למתמטיקה חשבון ורק התחילה ללמוד על מספרים לא שלמים הוכחה של נוסחה שלמדתי בכיתה י' אז גם הראיתי לה שהיא מסוגלת להבין דברים שגדולים ממנה לא תמיד מבינים וגם (אני מקווה) נטעתי בה את האהבה, הסקרנות והיופי שבמקצוע. התחושה היא שהמאמר "זורק" עובדות (שגם הם שנויות במחלוקת) ולא מספר סיפור. אני ממליצה לך לקרוא ספרים כמו "קיצור תולדות הזמן " ו"המשפט האחרון של פרמה" כדי לקבל השראה כיצד להביא לפופולריזציה נכונה של תחומים אלו.
אהוד ואדםאדום:
האמת היא שההוכחה הישיר של העניין הרבה יותר פשוטה.
לפני שאתאר אותה אציין שלדעתי זו באמת דוגמה שקטנה על גאוס וגם אני מצאתי את הנוסחה הזו לבד בעודי בבי"ס יסודי.
פשוט – הסכום של הראשון והאחרון זהה לסכום של השני והלפני אחרון וכן הלאה. כל הסכומים האלה הם N+1
אם המספר הוא זוגי יש N חלקי שתיים זוגות ולכן הסכום הוא N חלקי שתיים כפול (N ועוד אחד).
קל לראות שהנוסחה נשארת נכונה ל N אי זוגי כי המספר האמצעי (זה שנשאר בלתי מזווג) הוא בדיוק (N ועוד אחד) חלקי שתיים.
זה נראה לי הרבה יותר פשוט – בין בשאר מפני שזה לא מחייב לדעת שום דבר על שטחים (מה גם שחישוב השטח אינו הוכחה אמתית אבל אין לי כוח להסביר לעומק מה ההנחה הבלתי מבוססת ששיטת הוכחה זו מתבססת עליו)
למדתי הרבה יותר מהתגובות מאשר מהכתבה עצמה… 🙂
תודה לכולם.
אהוד, דוגמא יפה, תודה
נשמע כמו אגדה אורבנית שמבוססת באופן רופף מאוד על חייו של רמנוג'אן.
מעניין מה אנחנו היינו עושים בתקופה ההיא לו הלהיבו אותנו על תחום המתמטיקה
והיה לנו את כל הזמן הפנוי שהיה ללא טלוויזיה / אינטרנט וכו'
קראתי פעם על מחברת מתמטיקה שהכילה נוסחאות ותרגילים מדהימים
שאיזשהוא גאון הודי כתב לאחר שגר שנים לבד ביער עם ספר מתמטיקה יחיד שהיה בידו
אגדה אורבנית ? … לא יודע
לירן,
כוונתי הייתה לעשות הפרדה ברורה בין פסקאות הפונות לקהל הרחב לבין פסקאות שנכנסות עמוק יותר לתוך החומר. ניתן למשל לבצע הסתרה שלהן, כך שכשמשתמש יכנס לדף, הוא יראה את הכתבה כפי שכתבת, ובמקומות מסוימים שבהם תרצה להרחיב, ניתן יהיה ללחוץ על המילה או הסימן שתיבחר והפסקה המורחבת תוצג. כך אף אחד לא ייבהל ומי שירצה להרחיב ידיעתו יוכל לעשות זאת על אותו דף ממש.
נהדר, תודה לירן.
אגב עניינה אותי מאוד השורה האומרת כי "טענה המעניינת העלתה השערה מבוססת כי מספר הפיתולים הוא הגורם העיקרי לגאונותו של אדם"
מעולם לא שמעתי על טענה שכזו, ואשמח לקרוא עליה יותר. האם יש איזה קישור שאוכל להעזר בו , או יותר טוב – סימוכין למאמר מדעי?
תודה
גדי:
ביחס לדברי הראשונים – אני מבין מה הפריע לך.
דברי בטאו בעיקר את זה שנעלבתי בשם הכותב ובמחשבה לאחור – מה שנראה לי פוגע היה הסגנון יותר מהתוכן.
אני חייב לומר שגם אני אינני מצטיין בלשון עדינה (בעדינות) אבל אני משתדל להצליף רק במי שנראה לי כפועל בחוסר יושר או מתוך זלזול באחרים ולא במי שסתם טעה או התבטא בצורה לא מושלמת.
ביחס לחידות – נתחיל בזאת:
נתון פאון שחלק מפאותיו שחורות וחלקן לבנות (הכוונה היא לפאות שלמות שכל אחת מהן לבנה או שחורה).
נתון שיש יותר פאות שחורות מלבנות אבל אין שתי פאות שחורות החולקות מקצוע.
הוכח שבכזה פאון לא ניתן לחסום כדור (למען הסר ספק, בביטוי "כדור חסום בפאון" הכוונה היא לכדור הנוגע בכל פאותיו של הפאון. כדור מכסימלי שאפשר "לנפח" בפאון קיים כמובן תמיד).
והנה עוד אחת:
נתונים N מספרים קטנים מאלף שהכפולה המשותפת המינימאלית של כל שניים מהם גדולה מאלף.
הוכח שסכום ההופכיים שלהם קטן מ 1.5
ולקינוח:
רבע מישור (נאמר – זה שנמצא מעל לציר X ומימין לציר Y ) מאורגן כמטריצה אינסופית (ימינה וכלפי מעלה).
מתחילים לכתוב את אברי המטריצה החל באבר שבטור השמאלי בשורה התחתונה במספרים טבעיים תוך שמירה על החוק הבא: מותר למלא אבר רק אחרי שכל השורה משמאלו וכל הטור מתחתיו מולאו ואז יש לשים בו את הטבעי הקטן ביותר שעדיין לא מופיע – לא בשורתו מצד שמאל ולא בטורו מלמטה.
מצא (והוכח) אלגוריתם יעיל שיאפשר לך להשיב במהירות על השאלה מהו המספר שיושב בטור I ובשורה J
הערה:
אני מעביר לך את החידות רק בשביל הכיף.
אני מבקש ממך לא לפרסם כאן את הפתרון כי אני משתמש בחידות מסוג זה כדי להעמיד חלק מן המתיימרים לעודף שכל במקומם ואינני רוצה לבזבז "תחמושת".
אם תרצה לדבר על חידות אלו או אחרות אתה מוזמן לבקש מאבי בליזובסקי את האימייל שלי ולהראות לו תגובה זו כביטוי להסכמתי לכך שאכן יעשה זאת.
אולי כי בהן אני מכיר את הנושא…
(בשמחה, תן אחת, ואפילו כמה).
גדי:
לדעתי, תגובה ראויה של מישהו שאוהב מתמטיקה ולא עקב אחרי התגובות הייתה יכולה להיות משהו בסגנון "נו, תן אחת לדוגמה".
אני קורא הרבה באתר הזה ובאתרים אחרים ואני חייב לומר שדווקא הכתבות של לירן בולטות ברהיטות ובבהירות שלהן. לא ברור לי איך דווקא בהן קופצים לך דברים לעיניים.
מיכאל, אף אחד לא מתאמץ. יש דברים שפשוט קופצים לעיניים (וההערה האחרונה לא ראוייה לתגובה, פרט לאבחנה שלא כולם עוקבים אחרי התגובות שלך או אחרי כל התגובות באתר בכלל).
המתמתיקאי מס' 1 בעולם הוא דר' אלכס ספיבק מאוניברסיטת ת"א שבזכותו עברתי אלגברה לינארית.
איזה מלך!
לירן:
אני חושב שמדובר בכתבה נפלאה שהיא חלק מסדרה נפלאה.
גם אני מתמטיקאי אבל ברורות לי המגבלות של כתיבת מאמר לקהל הרחב.
יותר נכך, אני אפילו נהנה משמיעת סיפוריהם האישיים של המתמטיקאים ואני בהחלט חושב שזו דרך מצוינת לחבב את המתמטיקה על הבריות.
אנשים רבים נוטים לראות במתמטיקאי גאון קר ומנוכר והצגתו כאדם היא לדעתי מעשה חשוב ביותר.
כלל לא מפליא שספרים שלמים בסגנון זה (כמו "סודות ההצפנה", "המשפט האחרון של פרמה" ואחרים) זוכים להצלחה רבה.
בכל טקסט כתוב אפשר למצוא פה ושם טעויות או דרכים לשיפור וזה שאנשים מתאמצים כל כך לעשות זאת כאן פשוט מדהים אותי.
ולכל חובבי המתמטיקה שהגיבו לכתבה זו:
במהלך תגובותיי באתר זה פיזרתי כאן כבר מספר לא קטן של חידות מתמטיות.
משום מה לא מצאתם לנכון להתמודד עם אף אחת מהן.
נשאלת, לכן, השאלה, מה באמת מניע אתכם?
האם החלטתם להעדיף את מקצוע הגהת המאמרים על המקצוע אותו אתם אומרים שאתם אוהבים?
תודה רבה על הכתבה המעניינת.
לדעתי, רצוי היה להביא לינקים להעמקה למעוניינים: במה דברים אמורים מבחינה מתמטית.
אני חייב להודות שקצת מצערת אותי הגישה הגורסת שבכדי לכתוב מאמר מעניין על מתמטיקה אסור שתהיה בו מתמטיקה. אז המאמר אמר שגאוס היה גאון מתמטי, טוב ויפה; באותה מידה היה יכול לומר שהוא היה גאון באינדרינולוגיה והיו לו פריצות דרך מרשימות בקסטרוניסופיניה ובתורת החמרמרים. העיקר שהקורא לא ייבהל ממספרים.
אייל – כפי שהדגשתי, אני לא רוצה להכניס אף משוואה או מידע תיאורטי ולו רק בגלל השם הרע שיצא למתמטיקה בארצנו. אתם צריכים להבין שמספרים מרתיעים הרבה אנשים, אפילו אם מדובר בשיטה בה השתמש גאוס לסכימת המספרים שהינה קלה ביותר, אך אם הייתי מכניס אותה – הקורא הממוצע היה חושב לעצמו – " אוף, עוד פעם משוואות והסברים " . אני מתעניין במתמטיקה כבר מאז התיכון וקורא על כך רבות. לא פעם ולא פעמיים ניסיתי להסביר כל מיני דברים מרתקים שעשו גאוס ודומיו לאנשים אחרים, סתם ככה כדי להראות להם מה זה גאונות, אבל הם פשוט לא מצליחים להבין אפילו דברים שנראים לי טריוויאלים לחלוטין, ומדובר בחבר'ה מלומדים אחד-אחד. אם אני רושם דברים מסויימים, אני קודם כל חושב איך זה יתפרש אצל הקורא הממוצע ולא זה המלומד, בוודאי שאני יכול לשלב את ההוכחה של גאוס בנוגע למינימום המרחק של השאריות ברגרסיה, אבל מה זה יועיל לאדם הממוצע ? למה פנסיונר שסתם מתיישב מול המחשב ורוצה להנות ממדע פופולארי אמור להבין מה זה רגרסיה או דיברגנץ ? אין ספק כי מדובר במהפכות בעולם המתמטיקה, אבל שוב – השאלה היא למי אתה פונה. קח דוגמא קטנה, בספרו על חדו"א לסטודנטים, בן ציון קון מביא את סיפור חייהם של לייבניץ וניוטון ב-5 שורות, האם זה לדעתך מספיק כדי להבין את תרומתם של השניים לעולם ? בוודאי שלא, אבל הוא רשם בקצרה כי המטרה שלו הייתה להוכיח משפטים ולא לתאר את אורח חייהם של אלו שהוכיחו אותם. זה שהוא השמיט חלק נרחב מהביוגרפיה של שני הענקים האלה לא מעידה על כך שהוא לא מכיר אותם או מזלזל בהם ח"ו, אלא לכל עניין יש את הזמן והמקום שלו.
אהוד – הזכרתי במאמר הזה את ספרו של אריק טמפל בל. זה אכן ספר טוב, יש בו קצת הגזמות אבל מרתק ממש, זה למשל ספר שמתאים לכל אדם ולא רק למתמטיקאים או כאלה שיש להם רקע מתמטי.
אני רוצה לתת לך דוגמא מהמקורות היהודים – אם קראת פעם את התלמוד, יכולת במהרה להבין כי הרוב המוחלט של הסיפורים שם מעולם לא התרחש למרות שהגיבורים בו היו אמיתיים לחלוטין. הרמב"ם מחלק את האנשים הקוראים בתלמוד לשלושה – יש את הקבוצה שהוא קורא לה – "המסכנים שהורסים את הדת" ובה חברים אנשים שחושבים שהסיפורים הם אמיתיים לחלוטין ואברהם אבינו באמת קפץ לתוך תנור בוער ויצא משם חי, הכל אמת. יש את הקבוצה השניה שהיא רעה גדולה לדת, וזאת קבוצת האנשים החכמים (בענייני מדע ולא דת) שטוענים כי עצם זה שהסיפור לא נכון היסטורית ולא הגיוני מבחינה פיסיקלית -אין טעם לקרוא אותו. ויש את הקבוצה השלישית שהיא מורכבת מהחכמים באמת, שהם קוראים את הסיפור התלמודי ומבינים שמדובר במשל שהתנאים והאמוראים הביאו כדי ללמד אותם מוסר השכל חשוב, אך השתמשו בדימויים וסיפורי עמים כדי להביא את הרעיונות הכבירים גם לעם הארץ שלא תמיד מצליח להבין פילוסופיה ופלפול ברמה גבוהה.
אריק טמפל בל רושם דברים שחלקם כנראה לא התרחש, אך השאלה היא במה זה פוגם בקריאה שלך ? האם במידה והיה משמיט דברים אלו ומכניס במקומם הוכחות למשוואות של גאוס, זה מה שהיה מניח את דעתו של הקורא הממוצע ? הוא בעצם בא לתאר לאנשים עד כמה חכמים ויותר חשוב – אנושיים היו המתמטיקאים האלה, גם להם היו אהבות כמו גלואה, גם הם יכלו להיות בדיכאון כמו הנריק אבל ועוד, וזה מה שחשוב. רשמתי שגאוס המציא את הסדרה החשבונית כי זה מה שקיבלתי מהמורה שלי ומה שרשום בביוגרפיות שקראתי עד כה. במידה וימצא כי מישהו אחר גילה את זה כמה שנים לפניו, האם זה יוריד מקרנו של הגאון ? הרי הגאונות שלו בסופו של דבר לא מתמצה במה שהוא עשה בגיל 7, אלא המאמרים שלו שאתה ואני ויתר האקדמאים קוראים ומתלהבים מהתחכום והמקוריות שבהם, זה מה שעושה אותו למיוחד, וזוהי בעצם מטרת המאמר, לגרום לאנשים להתהלב מגאוס וידידיו ולרצות לדעת עליהם יותר, גם מבחינה היסטורית אך בעיקר מהבחינה המתמטית, אנשים צריכים להבין שמתמטיקה יכולה להיות דבר נפלא וחבל שעושים לא כזה שם רע אצלנו. אני כמובן לא טוען נגדך ספציפית, בוודאי שלא, אני מכוון לעבר הרוב שנמצא בישראל, וכן – הרוב לא ממש אוהב מתמטיקה ולא ממש מבין במתמטיקה, אז בכדי להגיע אליו אני לא רוצה להשתמש בנוסחאות גם אם הן הכי קלות להבנה, אני רוצה להשתמש במילים בלבד, בשפה שכולם יכולים להבין.
יגאל – תראה, בקשר ליאנוש בולייאי, בוודאי שיש חשיבות לעובדה שהוא בנו של פרקש היות והאחרון היה חברו היחיד והטוב ביותר של גאוס. הקשר בין השניים מתואר באריכות בביוגרפיות אחרות שמצאתי, אך הוספה של מידע הייתה גורמת לקורא הממוצע לסטות מהעיקר והוא – גאוס. אני מתכוון, אם יתאפשר לי, להביא עוד הרבה מיני-ביוגרפיות לאתר המצויין הזה, בעיקר מהתקופה של ימי הביניים עד המאה ה-19. אני רוצה שאנשים יקראו את הכתבות ויעשו קישורים בין אחד לשני כדי לקבל פרספקטיבה על יחסי הכוחות בין המתמטיקאים מבחינת זמן, מקום ועוד, המטרה היא להראות את המתמטיקאים כאנשים ולא כמחשבונים. מן הסתם הקורא הממוצע יכול להבין מתוך דברי כי היה מתח רב בין גאוס לבולייאי הבן שכן שניהם התחרו על המצאתה של הגיאומטריה החדשה, וזה לדעתי מה שיעניין את הקורא, התככים בינהם, מאבקי הכוחות ולאו דווקא העובדה שבמרחב כדורי קווים מקבילים יכולים להיפגש בשלב מסויים, זה לא העיקר.
בנוגע לעריכת הטקסט, אני מעיין בו לפחות 3 פעמים וגם שולח לעיונה של אישתי. אני משתדל לעשות כמיטב יכולתי בהיה ועריכה של הטקסט אך אינני יועץ לשוני או עורך מיומן בכדי להביא את המוצר למאה אחוז מבחינה צורנית. בכל אופן, אני משתדל לתקן כל פעם את הטקסט בהתאם למה שאתם אומרים פה ולכן חשובים לי הערותיכם, חיוביות ושליליות.
כפי שאמרתי בעבר וכאן אסיים – מבחינתי מספיק שנער צעיר שיקרא את המאמרים האלה יקבל השראה מהענקים הללו ויתחיל ללמוד מתמטיקה לעומקה, מי יודע – אולי גלואה השני מתסתתר לו איכנשהו ואנחנו לא יודעים. אני משתדל לעשות את כל מה שאני יכול מהצד שלי. אני לא מתמטיקאי אך יש לי רקע מתמטי די טוב, וכך הם פני הדברים. קבלו את המאמרים בקלילות ולא בראיה ריגורזית כפי שנדרש כשמדובר בהוכחה מתמטית, זאת לא המטרה כאן.
ידידי, בקרוב אעלה את המאמר השלישי. הפעם אעסוק באחד מענקי המתמטיקה האיטלקים. אשמח לשמוע את תגובותיכם גם למאמר זה.
תודה ולילה טוב,
לירן זיידמן
לירן,
הנושאים שאתה מכסה מעניינים אולם שתי בעיות קטנות מןרידות מעט מפוטנציאל ההנאה מהמאמרים:
1. התפרשות מיותרת לכיוונים לא חשובים (…שהיה בנו של… אשר…) ולא רלוונטיים.
2. חסרה עריכה של הטקסט (אולי מספיק שתקרא שוב את הטקסט שכתבת ותעיין בו כקורא מהצד).
בהצלחה
כל הכבוד על היוזמה!!!
מכיון שאתה מעונין בבקורת אעיר כי גם לי הפריעו אי דיוקים מסוימים.
אגב אני תמהה על כך שטענת כי גאוס הילד המציא תחום חדש במתמטיקה בכך
שסכם במהירות את כל המספרים עד מאה.
לנוסחא לסכום ישנו הסבר גרפי פשוט ויפה שניתן להסבירו גם לתלמיד יסודי.
פשוט מציינים את המספרים על ידי נקודות ורושמים את הנקודות בסדר עולה כך
שבראש מצד ימין נקודה מתחתיה שתי נקודות
וכך הלאה… אם מתחילים את רישום הנקודות באופן אחיד מימין מתקבל משולש
שבסיסו המספר האחרון בסכום ,n וכך גם גובהו משלמים את המשולש למלבן על ידי
הוספת משולש נוסף מחשבים את שטח המלבן ומחלקים בשניים: n(n+1)/2
0
00
000
0000
מוסיפים משולש נוסף
0****
00***
000**
0000*
מחשבים את השטח ומחלקים בשניים.
הערה אולי ניתן לשים קישור לאתרים נוספים לבעלי הענין המיוחד.
אגב אני מניח שאתה מכיר אבל ישנו ספר קנוני על ההיסוטוריה
של המתמטיקה: "Men of Mathematics" שנכתב על ידי
E.T. Bell
שוב עלה והצלח וכל הכבוד על היוזמה, שני הפרקים הראשונים היו מרתקים.
היי לירן, דוגמה או שתיים ל"עילגות" שאינה קשורה למתמטיקה:
"בגיל 18 התחיל את דרכו באוניברסיטת גטינגן שם הכיר את חברו היחיד פרקש בולייאי, שבנו , ממייסדי הגיאומטריה הלא-אוקלידית עתיד להיות גם הוא מגדולי המתמטיקאים בכל הזמנים."
יש כאן רווח לפני פסיק, וחסר רווח אחרי "הלא אוקלידית" (אולי לא הכרחי, אבל בהחלט משפר את הקריאות). פרט לכך יש כאן הקצנה לא מוצלחת של בולאי (מתמטיקאי חשוב, אבל אם הוא מהגדולים שבכל הזמנים, יש מאות גדולים בכל הזמנים).
אלו דברים שבאופן עקרוני אמורים להיות מטופלים בידי עורך, ולדעתי הם לא הבעיה המרכזית כאן. כאמור, אמירות סטייל זו על המקבילים לא נראות לי חסרות או מוזרות, אלא פשוט שגויות, מטעות ומבלבלות. אני מאוד מעריך את הכוונה הטובה שלך ובטוח שרבים מהקוראים ייהנו מהמאמר ויסתקרנו ואני שמח על כך; אני פשוט חושב שאתה מסוגל לעשות זאת טוב עוד יותר.
רעיון- אפשר אולי לכתוב מאמר שפונה גם לאדם הממוצע וגם ליותר מלומדים. אלו גם אלו נכנסים לאתר זה. איך? למשל- ניתן לשתול הרחבות בצבע שונה כך שמי שלא בקיא או לא מעוניין, ידלג עליהן.
היי לירן,
נהניתי לקרא ומחכה להמשך הסדרה.
לגבי יסודות הכלכלה, ככל הנראה היא באמת בלבלה במוח.
היא בסה"כ היתה צריכה להסביר שהעשירים הולכים ומתעשרים והעניים נשארים עניים….
היי נקודה,
קודם כל תודה על התמיכה.
אני חייב לתקן – הם לא מבלבלים את המוח. כפי שרשמתי, אני מאמין שהם מלומדים ולכן מסתכלים על המאמר הזה בפרספקטיבה שונה מאדם אחר ולכן הדברים נראים להם מוזרים או חסרים.
לפני כשנה המרצה שלי לכלכלת-מאקרו שהיא פרופסור במחלקה אצלנו, הוזמנה לראיון אצל לונדון וקירשנבאום בנוגע למצב הנורא ששרר באותה תקופה בעולם. היו לה כ-5 דקות להסביר לקהל צופים מנומם ובעל השכלה תיכונית את עיקרי תורתו של אבי הכלכלה המודרנית ג'ון מיינרד קיינס. במהלך הדיאלוג היא ניסתה להסביר מושג הקרוי אצלנו בכלכלה "מכפיל קיינסיאני" והוא בעצם יסוד היסודות של כל מחשבה כלכלית ברמת המאקרו ומן המונח הראשון שלומדים בתואר. לי ככלכלן היה ברור בן רגע למה הכוונה, אבל לאבא שלי שישב לידי נדרשו הסברים "ילדותיים" ולא מדוייקים ממש כפי שהיא נתנה מכיוון שכדי להבין זאת צריכים להניח כל מיני הנחות מסוימות ונוסחת המכפיל אמורה להיות מול עיניך. אם הייתי דוגל בשיטת הכותבים החולקים עלי, הייתי יכול לטעון כי הבנתה בכלכלת-מאקרו לוקה בחסר, אך דבר זה ישמע קצת בעייתי היות והיא הייתה חברה קבועה בצוותו של פול קרוגמן זוכה פרס נובל לכלכלה השנה.
לפני שרשמתי את המאמרים האלו שוחחתי עם העורך והגשתי כי איני מתכוון להוסיף כל נוסחא או ביטוי מסובך למיני-ביוגרפיות שארשום מכיוון שאתר זה פונה בין היתר לאוכלוסיה שלא נמנית עם פסגת האקדמיה הישראלית, וזה דבר מבורך מאוד, כן ירבו אתרים שכאלה. לכן, צריך לפנות לקוראים באופן בו יקבלו "טעימה" ולא הסבר, גם אם הטעימה הזאת לוקה בחוסר דיוק, מכיוון שבסיס הדברים הוא נכון אך דיוק הדברים רק יהרוס במקום להועיל, אפילו אם מדובר בנוסחא פשוטה יחסית.
אני תקווה שאנשים ממוצעים יקראו את הכתבות האלה ויגידו לעצמם – " ואו, איזה חכם הגאוס הזה, ואיך גלואה נהיה כזה גאון בגיל שאני הייתי לומד משוואות עם נעלם אחד , מה כל כך עניין אותם במתמטיקה שהם הקדישו לכך את כל החיים ? איך באמת הממצאים שלהם משפיעים עלינו ביום יום ? "
אם אני אצליח לגרום לאדם אחד לחקור את הדברים על בוריים, עשיתי את שלי. ומי יודע, אולי יש עוד גאונים עם פוטנציאל שלא מומש מכיוון שלא היה להם כיוון מעניין והיו זקוקים לדחיפה קלה.
לירן אני איתך….
הם סתם מבלבלים במוח.
תגובה נוספת :
גדי – בהמשך לדברי הקודמים רציתי לבקש בנוסף גם הבהרה לגבי המונח "עילג", האם מדובר ברמת עברית נמוכה או טעויות תחביר ? אם כן, אשמח לקבל הערות גם בנושא זה.
מקסים – אם תעביר הרצאה באקדמיה הגרמנית למתמטיקה בה למד לייבניץ ותציין כי ניוטון הוא זה שהמציא את הקלקולוס, מה לדעתך תהינה התגובות לכך ?
בנוגע להודו, טענות רבות גם הושמעו על יכולתם של המצרים הקדמונים (פפירוס אחמס) במציאת משוואות אלגבריות מהצורה המוכרת לנו כיום, אך בדיקה מעמיקה תביא אותך למסקנה כי אלו דברי הבל. הקונספציה של משוואות כמו שלמדת בתיכון או אקדמיה הובאו לידי הקהילה המלומדת רק בסביבות ימי הביניים על ידי מתמטיקאים כמו פרנסואה וייטה וחבריו.
ספייק – כמו שציינתי, אשמח לשמוע הערות וביקורת, אך קשה לי לאמוד את טיבו של מושג מופשט כגון "ציפיתי" משום שלא פרטת אלו ציפיות היו לך ממאמר שהוא כתבה בעיתון ולא מאמר מדעי גרידא.
המטרה שלי היא לא ללמד מתמטיקה ולעמוד על דיוקן של הגדרות ונוסחאות, אלא לתת טעימה מהעולם הזה לאנשים ממוצעים על מנת שיקראו ביוגרפיות נוספות ויעסקו במתמטיקה עצמה אם דבר זה יתאפשר להם.
היי לירן. אין לי ויכוח עם הצורך לכתוב באופן שיהיה קריא לקורא ההדיוט ולא על כך "התלוננתי" – מה שמפריע לי הוא כתיבה של דברים שגויים, או כתיבה של דברים חסרי משמעות.
עם זאת, אתה מעלה נקודה טובה – מה בעצם מבין הקורא ההדיוט מקריאת מאמר שבו זורקים לו בעיקר הרבה שמות מפוצצים של תחומים שבהם גאוס התעסק? התחושה שלי היא שלא הרבה – רק שגאוס היה מישהו חכם שהתעסק בהרבה דברים עם שמות מפוצצים. הוא שומע שגאוס "הוכיח את חוסר ההקבלה של קווים מקבילים", ומה הוא מבין מזה? כלום; רק שגאוס הוכיח את חוסר ההקבלה הנ"ל, מה שלא אומר לו שום דבר (חוץ אולי מ"קווים מקבילים הם לא באמת מקבילים", מה שקצת מבלבל – לא?)
אם כן, אולי בכל זאת כדאי לעשות מאמץ כלשהו להסביר את מה שגאוס עשה באמצעות מילים פשוטות (כמובן, לא באמצעות העתקה מהרצאות של מתמטיקאים שמיועדות למתמטיקאים אלא באמצעות העבודה הקשה של תיאור נכון של עובדות מתמטיות באמצעות מילים ודימויים קלים להבנה), ומכיוון שהיריעה רחבה, להתמקד בשניים-שלושה דברים מרכזיים (הגאומטריה הלא אוקלידית היא דוגמה טובה; ואת סכום הטור החשבוני שגאוס גילה באופן עצמאי אפשר להציג גם לקורא ההדיוט ללא קושי רב – אפילו ילד יכול להבין את הרעיון).
מסכים עם השניים הראשונה ובנוסף על כך ציפיתי ליותר גאוס היה אכן אחד הגאונים הגדולים מאז ומעולם ומגיע לו סיכום קצת יותר רציני!
שלום גדי.
כפי שציינתי בתגובה על גלואה, אני אשמח לקבל כל דעה, הערה וביקורת מצד הקוראים אפילו אם היא שלילית כפי שמובן מתוך דבריך. בהתאם לכך, ארצה להגיב בקצרה :
המטרה של המאמרים האלו היא להביא את עולם המתמטיקה לקבוצת האנשים המהווה רוב, לצערי, בחברה שלנו שבה מתמטיקה נחשבת קשה ומשעממת. גישה לקבוצה כזו שמה דגש יותר על כתיבה מעניינת ומליצית מאשר מתמטית/מושגית. ככלכלן, אני מכיר את שיטת הריבועים הפחותים על בוריה ואת עיקריה החשובים של התורה הדיפרנציאלית החלקית שהיא בסיס לכל תאוריה כלכלית רצינית, ובוודאי גם את שיטת גאוס-ג'ורדן למציאת דטרמיננטות, ונכון – גם אני הבטתי בהתפעלות במתמטיקה הזאת שלמדתי ממרצי באקדמיה, אך האם לדעתך הקורא הממוצע היה ממשיך לקרוא את המאמר שלי במידה והייתי משלב מילים שכאלה ? האם אתה סבור כי ניתן להסביר מה זה דיפרנציאל או אינטגרל לאדם הממוצע מחוץ לכותלי האקדמיה ? שמתי לעצמי מטרה במאמרים אלו לא להכניס משוואות ומונחים לועזיים שיכולים להבריח במהרה את הקורא שאינו בקיא במתמטיקה.
אותו כנ"ל לגבי גיאומטריה אי-אוקלידית. אני מניח בסבירות גבוהה כי רוב האנשים שקראו את המאמר הזה נתקלו בחייהם רק במקרה של קווים מקבילים כמו שהעלה אוקלידס.כמ כן, אתה יכול להניח שאני מכיר את האקסיומה החמישית שלו כיוון שהיא מהווה אבן דרך חשובה בעולם המתמטיקה, אך האם לדעתך מישהו מבין הקוראים היה מבין את ההגדרה המקורית ? בנוסף לכך, הייתי יכול להעתיק את תוכנה המלא של הרצאתו הידועה של רימאן בנוגע לאי-ההקבלה של קווים וסכום הזוויות במשולש במרחב כדורי , אך מה היה מפיק מכך תלמיד תיכון או פנסיונר שוחר ידע שהיו מגיע במקרה למאמר הזה ?
ידידי, על פי דבריך אני מאמין שאתה מלומד. לכן בקשתי היא אחת – זכור את ההנחיות לכתיבת סמינריון באוניברסיטה : הבודק לא מכיר את החומר ואתה צריך להסביר הכל (מודגש פעמיים) בצורה שתהיה ברורה לקורא הסביר הלא מלומד.
גאוס ראוי להרבה מאמרים עליו, תחומי הפעילות שלו הם כל אחד עולם מרתק בפני עצמו וקשה לי להאמין שיש אדם המסוגל להעיד על עצמו כי הוא מכיר את כל כתביו של גאוס כך שיוכל לרשום ביוגרפיה מלאה. למרות שעורך האתר לא מגביל אותי במקום, אני תמיד שומר על 2 עמודי WORD, שוב – בכדי לא לשעמם את הקורא.
מקווה שהצלחתי להבהיר את הנקודות השנויות במחלוקת,
לירן זיידמן
מסכים עם גדי!
גם אני חושתי בכך בזמן הקריאה.
וגם ישנם אי-דיוקים למשל:
שגאוס "המציא" ענף חדש, איזה בדיוק? סדרות חשבוניות?
גם ידוע שהוא אינו הראשון לזהות תבנית זו.
היום קראתי שגם בהודו במילניום הראשון, "הנוסחא" למציאת סכום סדרה חשבונית הייתה ידועה.
הכוונה שמאחורי המאמר יפה, אך הביצוע רע. המאמר פשוט עילג בחלקים שלו, ומבלבל בחלקים אחרים. למשל, להגיד "הוכיח את חוסר ההקבלה של קווים מקבילים" או להציג את אקסיומת המקבילים כפי שהוצגה זה פשוט שגוי ומטעה (מה שנכון הוא שאקסיומת המקבילים אומרת, בערך, שבהינתן ישר ונקודה מחוצה לו, ניתן להעביר לישר מקביל אחד ויחיד העובר דרך הנקודה – בגאומטריות הלא אוקלידיות זה אינו מצב העניינים). גם להגיד שמשוואות דיפרנציאליות חלקיות זה "כמו הנגזרת שלמדנו בתיכון אך עם עוד כמה משתנים" זה שגוי ומבלבל וכו' וכו'. גאוס ראוי למאמר שעושה יותר מאשר לזרוק ערב רב של שמות מסובכים של תחומים שהוא עסק בהם ואפילו לא מסביר כיאות מה התחומים הללו.
יש לציין שלולי גאוס ורימן, ספק אם אינשטיין היה מספיק להשלים בחייו את תורת היחסות הכללית.
כתבה מדהימה.
סיכמנו עליו רבות ,אך כעת הוספת לנו עוד.