במאמר זה אנסה לחשוף את הקוראים הן לחלק מדרכי החשיבה המתמטית והן ליופייה של המתמטיקה.

יוצאים מן הקופסה כדי להיכנס אליה:
מוקדש להרמן באר – מוח חקרני ותוסס כשל נער בגוף בן 94
במסגרת הדיונים סביב סדרת מאמריו של לירן זיידמן על המתמטיקאים הגדולים, יצא לנו גם לדון בשאלה מהו צירוף הנסיבות האופטימאלי ל"יצירת" מתמטיקאי טוב.
כיוון שכדי לדעת כיצד "ליצר" מתמטיקאי טוב יש לדעת מהו מתמטיקאי, וכיון שלא כל המגיבים הפגינו ידיעה כזאת, התקבל אצלי הרושם שיש מקום לשפר את ההיכרות של חלק מקוראי האתר עם דרכי מחשבתו של מתמטיקאי.
רושם אחר שהתקבל אצלי הוא שיחסם של אנשים למתמטיקאים מוכשרים מבוסס בעיקר על הערצה כלפי מי שמסוגל לבצע משימות מחשבתיות מורכבות ולא על התפעלות מיופייה של המתמטיקה עצמה.
במאמר זה אנסה לחשוף את הקוראים הן לחלק מדרכי החשיבה המתמטית והן ליופייה של המתמטיקה.
אנסה לעשות זאת באמצעות הדגמת פתרונה של חידה מתמטית סבוכה למדי – בדרכים אלמנטאריות – כאלו שכל תלמיד תיכון אמור להבין – וללא כל התבססות על ידע מתקדם.
החידה:
הוכח שלמלבן שניתן לרצפו באמצעות אוסף מלבנים שלכל אחד מהם לפחות מימד אחד שלם (כלומר – מידתו של אותו ממד היא מספר שלם של יחידות מדידה), חייב להיות לפחות מימד אחד שלם (באותה יחידת מדידה).
אוכיח את הטענה בשלוש דרכים שונות שכל אחת מהן מפגינה פנים שונות של המתמטיקה.
אציג את ההוכחות בסדר "כרונולוגי" – כלומר – בסדר בו עלו במוחי.
רצה הגורל וסדר זה הולך דווקא מן הקשה אל הקל אבל כיוון שאין קשר בין הפתרונות השונים, אין לדבר חשיבות.
אני ממליץ, עם זאת, לקורא שהתייאש מהבנת אחד הפתרונות, לדלג לפתרון הבא שאני מאמין שיהיה קל יותר להבנה.
אני די בטוח שההוכחה האחרונה תהיה מובנת לכל הקוראים.
הוכחה ראשונה:
זו ההוכחה הראשונה שחשבתי עליה. היא עלולה להיראות קצת מסורבלת אבל יתרונה הוא בכך שהיא ניתנת להרחבה פשוטה למספר כלשהו של ממדים.
ההוכחה היא בדרך השלילה.
בהוכחה מסוג זה מניחים שמסקנת המשפט אינה מתקיימת ומראים שהנחה זו מובילה לסתירה.
נתבונן במלבן ששני ממדיו אינם שלמים.
נמלא אותו בריבועים שצלעותיהם באורך 1 (ונרשה לעצמנו להשתמש גם בכמה שברי ריבועים לפי הצורך). נתחיל את המילוי מן הפינה השמאלית התחתונה.
התוצאה תיראה כך:
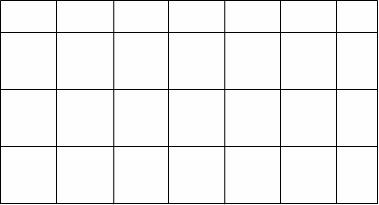
אחר כך, נתחיל את אותו תהליך מן הפינה הימנית העליונה.
התוצאה תיראה כך:

כל הריבועים המקוריים (שחור) חולקו באופן זהה לארבעה חלקים.
נתייחס אל כל המלבן כאל חלקת קרקע ונתמחר את פיסות הקרקע השונות על פי מיקומן בתוך הריבועים המקוריים באופן הבא (הריבוע השחור מצויר בהגדלה מסוימת כדי שיהיה מקום לכתוב בתוכו):
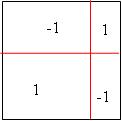
כלומר, כל מלבן בתוך הריבוע הנ"ל יקבל את המחיר 1 או -1 כאשר הוא נמכר בשלמותו וכאשר מוכרים חלק ממנו יקבע ערך אותו חלק על פי חלקו היחסי במלבן.
כל החלקות בתוך כל הריבועים השחורים תתומחרנה באותו אופן.
קל לראות שבתמחור זה, כל מלבן שאורכו או רחבו מספר שלם עולה בדיוק… אפס.
הקורא החכם מתבקש להשתכנע בכך בכוחות עצמו (הדרך לראות זאת היא לחלק את המלבן על ידי קווים שהם בכיוון הממד השלם, למלבנים צרים התחומים בין שניים מן הקווים השחורים באותו כיוון בתמונת המלבן הגדול שלעיל).
זה אומר שאם ניתן לכסות את המלבן הגדול באוסף מלבנים בעלי מימד אחד שהוא שלם אז מחיר המלבן כולו הוא אפס.
אבל אם נחלק את המלבן (ששני ממדיו אינם שלמים) על פי החלוקה הבאה:

נראה שכל אחד מהמלבנים המסומנים (על ידי מרקם ייחודי לכל מלבן) הוא בעל מימד שלם אחד לפחות ולכן עולה אפס ומכך נובע שערך המלבן המלא שווה לערכה של החלקה הבלתי מסומנת שהוא 1 .
מסתבר, אם כן, שההנחה שניתן למלא מלבן ששני ממדיו אינם שלמים במלבנים בעלי מימד שלם מובילה לסתירה שעל פיה מחיר הקרקע כולה שווה לאפס, מחד ולאחד, מאידך.
לכן אנחנו מסיקים שאם ניתן למלא את המלבן במלבנים בעלי מימד שלם הרי שהוא עצמו חייב להיות בעל ממד שלם וזה מש"ל.
ברבות הימים הראה לי מישהו הוכחה המתבססת על אינטגרלים כפולים של סינוסים וקוסינוסים שעובדת מאותה סיבה בדיוק.
היתרון של הדרך שלי הוא בכך שהיא יותר אלמנטארית (אינה דורשת רקע מתקדם במתימטיקה), יותר ישירה (ברור לכל אחד מדוע היא עובדת) ויותר קלה להרחבה למספר גבוה של ממדים.
הוכחה שניה:
הוכחה זו פשוטה ואלגנטית אך הרחבתה למספר כלשהו לממדים, אף כי אפשרית, מסובכת יותר.
נניח שיש לנו מלבן הממולא במלבנים קטנים יותר שלכל אחד מהם לפחות ממד שלם אחד.
בכל אחד מהמלבנים הפנימיים, נצבע את הצלעות שבכיוון השלם (אם יש למלבן שני כיוונים שלמים, נבחר רק אחד מהם לצביעה ונתעלם משלמותו של השני).
מכיוון שהמלבנים גובלים זה בזה יהיו קטעים שיצבעו פעמיים. לא נתעלם מעובדה זו – קטע שצבוע פעמיים ניתן יהיה לזהות כצבוע פעמיים.
נתבונן בדוגמה להמחשה:
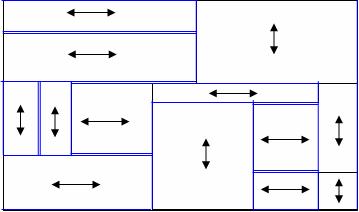
בדוגמה שלעיל סומן הכיוון השלם (היחיד שהיה או זה מבין השניים שנבחר) בחץ דו כיווני.
קטעים שנצבעו פעמיים מופיעים כקו צבוע כפול.
נניח עכשיו שאנו מתחילים ללכת על הקווים הצבועים ללא חזרה (מוחקים את הצבע מכל קטע שעברנו בו, אבל אם חלק מן הקטע צבוע פעמיים מוחקים רק את אחת הצביעות) כשאנחנו מתחילים את דרכנו בפינה השמאלית התחתונה של המלבן החיצוני ועוברים מקטע לקטע רק במקום בו הקטע עליו הלכנו מסתיים והקטע הבא מתחיל (אבחנה זו חשובה בגלל שקטעים יכולים לחפוף באופן חלקי, כפי שרואים גם בדוגמה).
קל לראות שבכל פעם שאנו מסיימים את טיולנו לאורך אחד הקטעים, אנו נמצאים במרחק שלם הן מן הצלע התחתונה של המלבן החיצוני והן מן הצלע השמאלית שלו (כי בכל צעד משתנה רק אחד המרחקים הללו והוא משתנה במספר שלם).
בשלב מסוים לא נוכל להמשיך להתקדם כי בכל פעם אנו מוחקים את הצבע מקטע נוסף ומספר הקטעים סופי.
אם נצליח להראות ששלב זה יקרה תמיד כאשר אנו בפינה של המלבן החיצוני ששונה מפינת המוצא של דרכנו אז נגיע באופן מיידי למסקנה הרצויה כי כזכור, גם בשלב זה, כמו בכל שלב בדרך, נמצא במרחק שלם הן מן הצלע תחתונה והן מן הצלע השמאלית.
כדי להראות שהמסלול חייב להסתיים באחת הפינות שאינה פינת היציאה, יש להבחין בעובדות הבאות:
– לפינת היציאה בוודאי שלא נחזור כי ברגע שיצאנו ממנה "שרפנו" את הקשר היחיד שלה עם שאר הנקודות.
– לעולם לא נעצור בנקודה שמספר הקטעים הצבועים המגיעים אליה הוא זוגי (כי בכל פעם שניכנס נצליח לצאת ואם עדיין יישארו קטעים צבועים המגיעים לנקודה מספרם יהיה עדיין זוגי כי הורדנו בדיוק 2 – קטע הכניסה וקטע היציאה – ממספר הקטעים הצבועים שהגיעו אליה קודם).
– הנקודות היחידות שמספר הקטעים הצבועים המגיעים אליהן הוא אי זוגי (למעשה בדיוק 1) הן הנקודות שבפינות.
את הטענה האחרונה בין שלשת הטענות הנ"ל יש כמובן להוכיח.
נוכיח זאת על ידי ניתוח של כל סוגי נקודות הסיום/התחלה של קטעים.
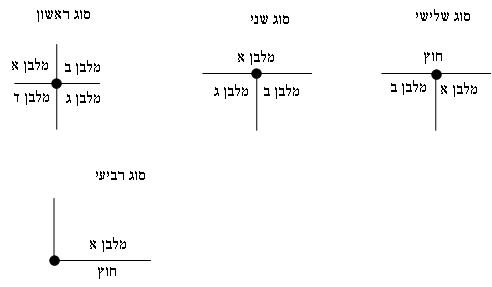
הנקודות מהסוג הראשון הן מפגש של ארבעה מלבנים. לנקודת הצומת מגיעים ארבעה קטעים צבועים – אחד מכל מלבן (זכרו שיתכן ששני קטעים צבועים ישכנו באותו מקום פיסי).
לנקודות מהסוג השני מגיעים 2 קטעים צבועים – אחד ממלבן ב ואחד ממלבן ג. אמנם עוברת בנקודה זו גם צלע של מלבן א (והיא יכולה גם להיות צבועה) אבל לצלע זו אין קצה בנקודה זו ולכן לא ניתן לעבור אליה או ממנה בנקודה זו.
לנקודות מהסוג השלישי מגיעים שני קטעים צבועים – אחד ממלבן א ואחד ממלבן ב.
הנקודות מהסוג הרביעי הן למעשה פינות המלבן החיצוני ואליהן מגיע, כאמור, בדיוק קטע צבוע אחד ויחיד.
מ.ש.ל.
שימו לב שהן דרך זו והן קודמתה נעזרות בתהליך המכונה במתמטיקה "בניית עזר".
בדרך הראשונה, בניית העזר היא תמחור הקרקע ובדרך השנייה זו צביעת הצלעות.
מי שלמד בתיכון על בניות עזר בגיאומטריה יכול לראות כאן שבניית עזר היא דבר הרבה יותר רחב שאינו מוגבל אפילו לעולם המושגים המקורי של הבעיה.
מי שלא למד בתיכון על בניות עזר, סביר שלמד בשנים האחרונות (עד כמה ששמעתי, החומר של תיכון כבר לא כולל בעיות בניה בגיאומטריה. זה בפני עצמו הפסד עצום לדעתי אבל לא ידוע לי אם בניות עזר עדיין "מותר" לתלמידים להכיר מבלי שיהרגו אותם על כך שהם יודעים יותר מדי).
הוכחה שלישית:
זאת בעיני הפשוטה והאלגנטית מכל הדרכים בהן הוכחתי את המשפט.
חסרונה הוא בכך שהיא קשה להרחבה למספר גבוה יותר של ממדים אך היא מכפרת על חסרון זה במסר נוסף שאפשר להמחיש באמצעותה כפי שתיווכחו.
נתבונן במלבן שמולא על ידי מלבנים שלכל אחד מהם מימד אחד שלם לפחות.
נוציא ממנו את כל המלבנים אך נזכור איפה היה כל אחד ונתחיל להחזיר אותם חזרה למקומם אחד אחרי השני.
בהחזירנו אותם למקומם נתחיל מלמטה ונקפיד על כך שכל מלבן יוחזר למקומו רק אחרי שיש על מה "להניח" אותו "בביטחון" כלומר שכל המלבנים ה"נושאים" אותו כבר הונחו.
להלן ציור להמחשה:

בציור שלעיל, המלבנים הלבנים כבר הונחו ואת האחרים עוד יש להניח.
את המלבן הירוק כבר אפשר להחזיר למקומו אבל את האדום עוד לא כי "הבסיס שלו" עוד לא מוכן בשלמותו (לפני שנניח את האדום עלינו להניח את המלבן המפוספס שנמצא תחת חלקו הימני.
בכל שלב, נגדיר בתור "חזית" את הקו המקוטע שמתאר את הנקודות הגבוהות ביותר שכבר מולאו.
למשל, בציור הנ"ל, לאחר שיונח המלבן הירוק, תתואר החזית על ידי הקו השחור העבה.
כל נקודה על החזית נמצאת במרחק מסוים מבסיס המלבן החיצוני.
מרחק זה יכול להיות שלם או שבור (בלתי שלם).
נאפיין את הנקודות שבבסיס המלבן החיצוני (להלן "הבסיס") כשלמות אם החזית שמעליהן נמצאת במרחק שלם מהן וכשבורות אם החזית נמצאת במרחק שבור מעליהן.
בהתחלת התהליך, החזית היא בסיס המלבן החיצוני ולכן כל הנקודות על הבסיס (הן במרחק אפס מהחזית ואפס הוא כידוע שלם ולכן הן) שלמות.
בכל פעם שמניחים מלבן נוסף עשוי אפיונן של חלק מנקודות הבסיס להשתנות.
אפיון של נקודה יכול להשתנות רק אם מניחים מלבן שגבהו אינו שלם (ואז אנחנו יודעים שרחבו שלם).
זה אומר שבכל פעם שמשתנה מצב של חלק מנקודות הבסיס זה קורה לקטע בבסיס שארכו שלם.
מכיוון שבתחילת התהליך כל הנקודות שלמות (כאמור לעיל) ומכיוון שכל שינוי באפיון של נקודות מתרחש תמיד על קטעים שלמים, אנחנו יכולים לטעון שבכל שלב מידת קבוצת הנקודות השבורות היא שלמה (בהתחלה היא אפס כי כל הנקודות שלמות ובהמשך, כשהיא גדלה או קטנה היא עושה זאת רק לאורך קטעים שאורכם שלם).
אז מה קורה בסוף?
בסוף אחרי שמילאנו את כל המלבן החיצוני, כל נקודות הבסיס במרחק זהה מן החזית ולכן או שכולן שלמות או שכולן שבורות.
אם הן שלמות אז גמרנו כי זה אומר שגובה המלבן שלם.
אם הן שבורות, גמרנו גם כן כי אנחנו יודעים שבכל שלב, כולל בשלב זה, מידת קבוצת הנקודות השבורות היא שלמה ופירוש הדבר הוא שמידת הבסיס שלמה כי קבוצת הנקודות השבורות היא כל הבסיס.
וואו!! לא?
מסתבר שאפשר לפתור את הבעיה פשוט על ידי….משחק מילים.
במאמר קודם טענתי שמותר האדם מן הבהמה, יותר משהוא מתבטא בעובדה שלאדם יש שפה, הוא מתבטא ביכולתו להמציא שפה.
יכולת זו עוזרת לו לחשוב כי הוא יכול לתת שם או סמל למושג מורכב ואחר כך להשתמש בשם/סמל הזה בבניית מושגים ומחשבות מורכבים יותר וחוזר חלילה.
נראה לי שבפתרון זה ניתן לראות כמה יכולת זו מועילה.
מחוץ לעולם הבעיה שלנו משמשות המילים "חזית", "שלם" ו"שבור" במשמעות שונה לחלוטין מאשר בתוך עולם הבעיה (מי שמע אי פעם על נקודה שבורה?).
עלי לציין שיכולתי לבחור מילים אחרות (כמו צפפוח, שמרגול ויפרן) לאותו צורך אבל העדפתי להשתמש במילים שיש קשר בין משמעותן המקובלת למשמעותן בתוך הבעיה.
הרחבות לחידה המקורית:
מסתבר שניתן להרחיב את המשפט למספר גדול יותר של ממדים.
בניסוחו המוכלל ביותר נראה המשפט כך:
אם יש לנו אוסף של תיבות N ממדיות (לא בהכרח זהות!) שלכל אחת מהן לפחות K מימדים שאורכם שלם הרי שלכל תיבה N ממדית שניתן למלא בהן לפחות K ממדים שארכם שלם.
לא אספק כאן הוכחה מדוקדקת של העניין כי הפורמליזם המתמטי יקשה על הקוראים.
תחת זאת, אסתפק בתיאור הרעיון של ההוכחה:
קודם כל נראה ששיטת ההוכחה הראשונה עוברת למימדים נוספים ממש ללא שינוי.
פשוט במקום לתמחר ריבועים בעלי צלע באורך יחידה על ידי חלוקתם לארבעה מלבנים, נתמחר "קוביות" N ממדיות על ידי חלוקתן ל"תיבות" N ממדיות ( 2N תיבות כאלו שכל אחת מכילה בדיוק קדקוד אחד מן הקובייה המחולקת).
קשה לצייר את זה אבל אתם מוזמנים לנסות לשוות בעיני רוחכם איך זה נראה בשלשה ממדים. התמחור מתבצע על ידי חלוקה של התיבה החיצונית לקוביות רגילות שכל אחת מהן מחולקת ל 8 תיבות שכל אחת מהן עולה 1 או -1 .
הציור הבא (של מה שאמור להיות קובייה תלת ממדית מחולקת ל 8 תיבות) עשוי לעזור:
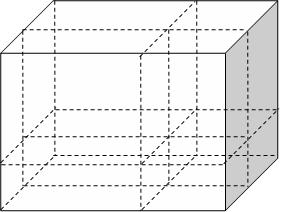
קשה לתאר בטקסט שנגיש לכל אחד את התהליך המדויק אבל אני מקווה שמה שאמרתי מובן בכל זאת.
ליודעי חן אוסיף שניתן לקבוע את מחיר התיבה פשוט על ידי העלאת המספר מינוס אחת בחזקת מספר האחדים בייצוג של פינת הקובייה המשויכת אליה (כאשר כל הפינות מיוצגות על ידי כל הצירופים האפשריים של N אפסים או אחדים).
בדומה למקרה הדו ממדי, גם כאן ניתן לראות שתיבה שאחת ממידותיה שלמה תעלה אפס וגם כאן נגיע לסתירה במקרה שבתיבה החיצונית אין ממד שלם.
מכאן נקבל שכאשר נתון אוסף תיבות N ממדיות בעלות ממד שלם, חייב להיות ממד אחד שלם לכל תיבה N ממדית שנרכיב באמצעותן אבל הרי רצינו יותר. עד כאן הוכחנו את המשפט עבור כל N אבל רק עבור K=1.
המעבר ל K גדול יותר הוא פשוט.
אם יש K ממדים שלמים לכל תיבה פנימית אז בוודאי שיש אחד כזה.
לכן צריך להיות לתיבה ה N ממדית, ממד אחד שלם.
נסתכל עכשיו על "פאה" המאונכת לממד זה – זוהי למעשה תיבה N-1 ממדית המכוסה על ידי תיבות
N-1 ממדיות שלכל אחת מהן לפחות K-1 ממדים שלמים ולכן גם לתיבה זו יש ממד שלם וכך הלאה.
כפי שציינתי, כתיבה פורמאלית מלאה ומדויקת של פתרון שאלות מסוג זה היא דבר מסורבל ביותר.
אני מקווה שהטקסט הנוכחי מספיק כדי לתת למי שאין לו את כל הבסיס הדרוש לפחות את ה"טעם" של ההוכחה ולמי שיש לו את הבסיס הדרוש את כל מה שנחוץ כדי להבינה במלואה.
מסקנות נוספות:
באמצעות תיבות שממדיהן 1x2x4 ניתן למלא רק תיבות שיש להן מימד שמתחלק ב 4, מימד נוסף שמתחלק ב 2 ומימד שלישי שלם (ואת כולן).
באופן כללי, באמצעות תיבות בעלות מימדים שהם כפולות שלמות של D1,D2,D3….DK אם DI מחלק את DI+1 ניתן למלא רק תיבות בעלות אותה תכונה.
באמצעות תיבות בעלות מימדים שהם כפולות שלמות של D1,D2,D3….DK כאשר היחסים בין המימדים אלה אי רציונאליים, ניתן למלא רק תיבות בעלות אותה תכונה.
בעלי הנטיות המתמטיות מוזמנים להוכיח לעצמם טענות נגזרות אלו.
המסקנה האחרונה אינה נכונה כאשר היחסים רציונאליים (כי אז מימד אחד של התיבה החיצונית יכול "לספק" כמה מימדים של הפנימיות).
הקורא הנמרץ מוזמן להשתכנע בכך על ידי בניית דוגמה.
בגיליון 112 של גליליאו הופיעה השאלה הבאה:
האם אפשר למלא תיבה שמידותיה 6X6X6 בתיבות שמידותיהן 1X2X4?
בתגובה לשאלה כתבתי שהתשובה עליה היא אחת המסקנות ממשפט כללי שניתן להוכיח שעל פיו אם יש לנו אוסף של תיבות N ממדיות (לא בהכרח זהות!) שלכל אחת מהן לפחות K מימדים שאורכם שלם הרי שלכל תיבה N ממדית שניתן למלא בהן לפחות K ממדים שארכם שלם (המשפט שבו עסק מאמר זה).
הסברתי גם כיצד נובעת התשובה מן המשפט אבל כאן אשאיר זאת כתרגיל (קל) לקוראים.

54 תגובות
זוכרים את תיאור הקשר בין היכולת להמציא שפה ליכולת לחשוב ביעילות?
הנה דוגמה יפה מן הימים האחרונים:
http://www.haaretz.co.il/news/science/1.1827725
"מוצ'יזוקי מפתח שפה חדשה ולכן יידרשו עוד כמה שנים טובות עד שיהיה קונסנזוס אם היא נכונה או לא",
לכל מי שמתעניין – יש טענה להוכחה ש P!=NP
להלן רשימת קישורים רלוונטיים:
http://www.hpl.hp.com/personal/Vinay_Deolalikar/Papers/pnp12pt.pdf
http://rjlipton.wordpress.com/2010/08/08/a-proof-that-p-is-not-equal-to-np/
http://rjlipton.wordpress.com/?p=5206
http://www.geekosystem.com/p-np-proof-vinay-deolalikar/
http://www.hpl.hp.com/personal/Vinay_Deolalikar/
נהניתי לקרוא.
אני מכיר ניסוח קצת שונה שמאפשר הוכחה מעט אחרת אבל באותם עקרונות בדיוק כמו ההוכחה השניה.
חפרתם
צביקי:
תודה על דבריך אבל יש דבר אחד שבו טעית בהבנת כוונתי.
כוונתי הייתה לאפשר למי שרוצה להעמיק את הבנתו את העניין – לקבל תחושה אמיתית אודותיו.
אין כל דרך ללמד בדרכי נועם את מי שאינו רוצה ללמוד ומאמר זה לא נועד לאנשים כאלה.
הדרך ללמד אנשים כאלה מתחילה בריסון הרשעות והיוהרה שלהם וזה מה שאכן ניסיתי לעשות בתגובות.
מיכאל היקר,
חן חן על מאמרך המחכים.
ברשותך אצטט חלק ממנה:
" מסתבר שאפשר לפתור את הבעיה פשוט על ידי….משחק מילים.
במאמר קודם טענתי שמותר האדם מן הבהמה, יותר משהוא מתבטא בעובדה שלאדם יש שפה, הוא מתבטא ביכולתו להמציא שפה.
יכולת זו עוזרת לו לחשוב כי הוא יכול לתת שם או סמל למושג מורכב ואחר כך להשתמש בשם/סמל הזה בבניית מושגים ומחשבות מורכבים יותר וחוזר חלילה.
נראה לי שבפתרון זה ניתן לראות כמה יכולת זו מועילה."
אני אכן מסכים עמך.
יחד עם זאת, יש לציין שיתרון זה רלוונטי כשבני האדם שאליהם מיועד המסר אכן מבין מושגים ומחשבות מורכבים אלו.
כשאינם מכירים, ואני חוזר שהכוונה היא לקהל היעד שציינת בתחילת הכתבה, נשל לו יתרון האדם ונותרה הבהמה, אשר כפי שראינו בתגובותיך, גם לה יש יכולות ביטוי לא קטנות.
צביקי
הי מיכאל. יצרתי הפניה לחידה ולמאמר היפה שלך בגן אדם
תודה מיכאל . זה מעניין. אתה ודאי יודע שהשנה נקראת שנת האסטרונומיה בגלל שחלפו ו 400 שנים מהתצפית הראשונה של גלילאו בטלסקופ באוניברסיטת פדובה. בהתאם לקישור המצורף נותרו ללא פיתרון 4 בעיות מהרשימה של 23 הבעיות של הילברט 6,8,12,16. אז למתמטיקאי יש עוד מה לעשות..
http://he.wikipedia.org/wiki/23_%D7%94%D7%91%D7%A2%D7%99%D7%95%D7%AA_%D7%A9%D7%9C_%D7%94%D7%99%D7%9C%D7%91%D7%A8%D7%98
תודה, משה.
האמת היא שאני חי את כל הבעיות היפות שאי פעם נתקלתי בהן וזו רק אחת מרבות.
אני מקווה להמשיך לחיות את כולן עוד הרבה שנים (אומרים שמי שמעשן 120 שנה חי הרבה מאד).
הרמן באר הוא סבה של העורכת הקודמת של כתב העת "גליליאו" – אחד מן האנשים שהקריבו את חלום ההתמקצעות במתמטיקה על מזבח בניית הארץ.
בגילו המופלג הוא עדיין אוהב לעסוק בבעיות מתמטיות וממשיך לנסות להבין את העולם.
שלומית עוזיאל – העורכת הקודמת של גליליאו חשבה שהשידוך בינינו עשוי לעלות יפה וכך אכן היה.
הי מיכאל
קראתי בעניין את המאמר היפה שלך "להיות מתמטיקאי" – תודה.
יפה בעיני שאתה חי בעיה מתמטית כבר כ 40 שנים !
אהבתי במיוחד את ההוכחה השלישית שהיא לדעתי האלגנטית ביותר.
מיהו הרמן באר, אשר שלו הקדשת את המאמר ?
משה
רון:
לצערי מה שקורה כאן דווקא ענה בדיוק על ציפיותיי.
יש כאן כמה מגיבים הגונים וכמה שאינם הגונים – בדיוק כמו בכל דיון אחר באתר.
בין אלה שאינם הגונים – יש מי שתקף אותי אישית וניסיון ההרגעה שלך לא יטייח עובדה זו.
למהמיאתה:
פעם – כשנשוחח – אסביר לך כיצד גיליתי מי אתה.
השמאל אינו מה שהימין חושב שהוא ובכל מקרה אני אינני מגדיר את עצמי כשמאלני מן הסוג שאתה חושב עליו.
הסברתי בהזדמנויות שונות שלדעתי האסטרטגיה של "מידה כנגד מידה" שהומחשה על ידי האלגוריתם Tit for Tat בניסוי של אקסלרוד היא האסטרטגיה הנכונה.
היה הגון – לעולם אל תתקוף ללא סיבה – אבל כשתוקפים אותך ללא סיבה – הענש בחומרה.
טוב הפוסט הזה ותגובותיו יצאו מכל פרופורציה
מיכאל ניסה משהו – וזה לא צלח כפי שהוא ציפה.
לא קרה כלום, אפשר לנסות שוב.
יש כאן בקורת על דרך ההצגה, לא התקפה פול און אישית עליו ועל יכולותיו
מיכאל קח את זה באיזי יש התקפות יותר בעייתיות…
http://www.youtube.com/watch?v=hiANsBkgqjU
רפי:
תודה על דבריך.
ביחס לשאלתך על האינטואיציה – ראה תגובה 24 שלי.
לצערי אין בה תשובה של ממש אבל זה כל מה שאני יודע לומר.
אם הייתי רמאנוג'אן הייתי אומר שהאלה נאמאגירי שתלה את הפתרון במוחי.
מיכאל רוטשילד:
אם באמת אתה יודע מי אני אפילו שאני בעצמי לא יודע מי אני אז אתה באמת גאון בעל אינטואיציה ממדרגה ראשונה.
ובעניין ההתנפחויות אני עדיין סבור שאפשר לפרגן לכל מתנפח מצוי ולאפשר לו לזקוף כרבולת מבלי להעלב.
חוץ מזה מתמיה שלדעתך מענה לאלימות באלימות. כי לתומי הצטייר שהנך בצד השמאלי שבמפה.
הרי זו בדרך כלל גישה ימנית ניצית. אבל יתכן גם שלצד השמאלי יש צד ימני בעצמו.
זה מסובך מידי אולי כדאי פשוט לאמץ גישה קלילה כשזה לא עולה כלום החיים מספיק קשים.
מיכאל לא רוטשילד:
אינני מסכים אתך.
המענה לאלימות צריך להיות אלימות שכנגד.
כשבא הסתם קורא הזה ושיחק את תפקיד גולדסטון מצאתי לנכון להבהיר לו את הדברים באופן הכי ברור שאפשר.
למהמיאתה:
מכיוון שאני יודע מי אתה – אני מתפלא על תגובתך.
על איזו התנפחות שלי אתה מדבר?
אני הוא זה שאמר שהשאלה עם המספרים מתאימה ליסודי מבלי שאדע לפתור אותה בעצמי?
ה"סטודנט" סתם תקף אותי אישית מבלי שעשיתי לו כל רע.
כפי שאמרתי – מלבד רעל הוא לא תרם לדיון דבר.
למיכאל רוטשילד-
תגובה לתגובה 30
אינני רוצה להכנס לעניין מי תקף את מי, מי מנסה להישתחצן ומי לא. אני רוצה להתייחס למשפט אחד, שכתבת בתגובתך, ואני מצטט: "בתגובה שלי לא היה שמץ יהירות – היה בה רק ניסיון לאפשר לחרא הזה לבחון את עצמו במשהו שכן שייך לנושא לפני שהוא תוקף אותי בתחומים שאינם שייכים לנושא".
אני חושב שככותב רשמי באתר, יכולת קצת להבליג בהתבטאויות שלך, לא לרדת לרמת הסטודנט מהישוב, ולא להשתמש במילה "חרא". זה לא מכובד, ולא מוסיף לרמת האתר.
שלום מיכאל,
רצוני להודות לך על ההשקעה העצומה בכתיבת המאמר. אחר קריאה מסקרנת מאוד הצלחתי להבין את יופיין של כל אחת מן ההוכחות.
בחירת הצעדים בכל אחת מדרכי הפתרון הייתה ייחודית ומעניינת ביותר. בעניין האינטואיציה המתמטית, אצטרף לשאלתו של אהוד.
בזמנים אלה אני נמצא בשלבי ההכנה לבחינת הבגרות במתמטיקה(שאלון 007), וזה כיך גדול עבורי לראות צדדים אחרים של המתמטיקה שלא מוצאים בדרך כלל את ביטויים במסגרת הלימודים בתיכון. אני אפילו שוקל ברצינות להמשיך בלימודי המתמטיקה שלי בטכניון.
אשמח לספוג עד מאהבת המתמטיקה שלך גם בעתיד.
מיכאל רוטשילד:
לא יודע מי אני אז איך אתה יודע מי אני.
הדברים מופנים לכל המתווכחים. גם אליך.
נדמה לי שאין כאן מתווכחת בחורה. מהסיבה הזאת שנשים נוטות פחות לנפח את האגו בדברים מסוג זה.
ובכל אופן אם מתנפחים אז לכולם מותר להתנפח. כל בעל כרבולת מוזמן.
גם הסטודנט העייף זקוק לעידוד וזכאי לו.
לא צריך להתקמץ בפירגונים.
למהמיאתה:
לפני שאענה אשמח לדעת למי מופנים הדברים.
אגב – אני דווקא יודע מי אתה 🙂
למה התוקפנות. אז מה אם סטודנט רוצה להתנפח מול מיכאל. כל אחד רוצה להראות שלו יש יותר גדול מה זה גן ילדים. זה בסך הכל מתמטיקה לא מלחמה. ואגב למה שאלת המספרים הטיבעיים אמורה להפחיד את הסטודנט. מתאימה ליסודי לדעתי.
מ.אותגר:
אולי לא הבנת את ההוכחות אבל שלא כמו חלק מן האחרים, לפחות הבנת איך מתנהגים כך שאין לך מה להתבייש.
אני מציע שתנסה להתמקד בהוכחה השלישית ולהתגבר על בעיית חוסר הריכוז שאתה מתאר.
נסה פעמיים שלש ואם עדיין לא תבין – נראה מה אפשר לעשות.
אין לי כל בעיה גם לפגוש אותך ולהסביר לך (בשיחה פנים אל פנים אוכל לעמוד הרבה יותר טוב על הקשיים שעוצרים אותך ולעזור לך להתגבר עליהם).
למעשה זו הזמנה פתוחה לכל מי שאינו מצליח להבין את המאמר ורוצה לקבל הסבר אישי.
לסטודנט מהישוב
הרשה נא לי להעיר לך כי, תגובתך (מס'-26) הינה לכל הפחות בלתי הוגנת ובלתי מנומסת. ראשית, הרי הכותב עצמו במאמרו עמד על "בעיית השפה" בבעיות מתמטיות בכלל ובבעיה הנדונה, בפרט. הוא הסביר כי מילים שמשתמשים בהן בבעיות מתמטיות מקבלות באמצעות הגדרתן המתמטית, משמעויות השונות ממשמעויותיהן בשפה היומיומית. שנית, המושגים המופיעים בבעיה הרי הוגדרו בגוף הבעיה. זאת הדרך המקובלת בשפת המתמטיקה. הלא אתה, המעיד על עצמך כאילו הנך סטודנט בטכניון, בוודאי נתקלת בכך פעמים רבות
במהלך לימודיך. לכן, לא ברורה לי טענתך כנגד הכתוב במאמר .
לבסוף הערה אבחנתית . לא אתפלא להיווכח כי אתה הנך סטודנט להנדסה ולא במקצוע מדעי כגון מתמטיקה או פיסיקה. אני אומר זאת מכיוון שלמיטב כושר האבחנה שלי, מהנדסים (ואדריכלים) מחפשים, לרוב, את האספקט הפרקטי,הישומי,המיידי ואת הטכניקה המהירה לקבלת ה"תוצאה הנכונה". אנשי מדע, לעומת זאת הינם בעלי תפיסה רחבה יותר. והם מחפשים את חוקים מוכללים ככל שאפשר לתאור כללי של בעיות. (הן בעיות פיסיקאליות והן עיוניות).
המדע והמתמטיקה הראו בעבר כי לעיתים דאווקא הגישה המוכללת
(כוונתי למה שמכונה הגישה האידוקטיבית) עשויה להוביל לפתרון מגוון רחב של בעיות.
אותגרתי…
בטח שהבנתי את החידה, מה (או שאולי בעצם לא?..)
מה שבטוח הוא שלא הבנתי את ההוכחות.
מצד שני, אין לי הכשרה מתמטית, דהיינו איני יודע לקרוא הוכחות שכאלה – חוט המחשבה שלי דק מדי, ואני שוכח מה השלב הנוכחי…
בעצם איני מבין את החלוקה לשלבים, ומה ההגיון הפנימי (כלומר, על איזו שאלה צריך לענות קודם, כדי לבסס ידיעה מספקת כתשתית לשאלה הבאה).
ייתכן שפסקה המתארת את הלך המחשבה או האינטואיציה שבבסיס כל הוכחה תעזור.
קורא סתם:
אני מניח שאם תראה מישהו שגונב למישהו אחר את הרכב וההוא רץ אחריו וצועק – תנזוף בזה שצועק.
האם לא קראת את תשובתו הנהדרת והמעמיקה של הסטודנט?
מה, לדעתך, הוא רצה להשיג בתגובה זו?
אין צורך שתטרח לענות – מספיק שתקרא כדי שתראה שהוא לא אמר שום דבר לעניין.
הוא לא התייחס לחידה ולא להסברים – כלום – הוא פשוט החליט שבא לו לתקוף אותי.
אני יכול להבטיח לך שגם במקרים האחרים שעל פיהם גיבשת את דעתך – הרקע דומה.
בתגובה שלי לא היה שמץ יהירות – היה בה רק ניסיון לאפשר לחרא הזה לבחון את עצמו במשהו שכן שייך לנושא לפני שהוא תוקף אותי בתחומים שאינם שייכים לנושא.
אני מייחס את אי הבנתך את העניין לכך שלא קראת את דבריו.
למיכאל,
חבל.
אני מכבד את ידיעותיך,אך לצערי בחלק מתשובותיך (בכלל – ולא רק הפעם) מסתתרת אי צניעות. ובתשובתך לסטודנט (7) מתגלה אף יהירות.
אפשר להתנצח – אבל למה להתנגח ?
אני רק רוצה להגיד שלא הבנתי כלום מהחידה ולא מהביקורות
אבל אני שמח שיש אנשים עם שכל בארץ
סטודנט מהישוב:
מאיזה ישוב אתה בדיוק?
תודה על תרומתך המרתקת לדיון הענייני.
תגיד לי, אגב:
בישוב שלך יודעים להוכיח שאם יש קבוצה של טבעיים בין אחד לאלף שהכפולה המשותפת המינימלית של כל שניים מהם גדולה מאלף אז סכום ההופכיים שלהם קטן מ 1.5?
אני מקווה שבישוב שלך לפחות יודעים שההופכי של מספר זה אחד חלקי אותו מספר.
תהיה בריא איזה ניסוח לחידה,
אני אומנם אחרי יום לימודים ארוך,
אבל בתור סטודנט בטכניון שרואה לא מעט הוכחות מתמטיות על בסיס יומיומי,
הייתי צריך להתאמץ כדי להבין את הניסוח של החידה, וגם את זה הצלחתי רק בגלל שקראתי את ההוכחות.
"מימד אחד שלם (כלומר – מידתו של אותו ממד היא מספר שלם של יחידות מדידה)" מה אמורים להבין מהמשפט הזה?
מה זה מימד שלם? מה היא בכלל מידה של מימד? אין כאלו מושגים.
חסרות הוכחות פשוטות ויפות עם סיפורים מעניינים? אפשר לדוגמא להראות את ההוכחה של אוילר על גרפים אוליריים, עם הסיפור של הגשרים בקניגסברג (ואפשר להסביר את זה בלי להסביר בכלל מה זה גרף).
מיכאל שוב תודה עלהכתבה היפה.
אני מאמין שכדי לשאוב הנאה מחידה יש לנסות לפתור אותה. רבים מן הקוראים לא ניסו לפתור את החידה ולכן היה קשה להם לראות את היופי בפתרון.
לגבי הקו החסר כאשר אני לוחץ על הציור בתחתית התמונה (כשי לקבל רק את התמונה) היא מופיעה כמו שצריך? רק כאשר התמונה הינה חלק מהכתבה נעלם בה הקו. נפךאות המחשב.
אהוד:
שמתי כרגע לב לכך ששכחתי לענות לך על הדבר שהוביל אותי לאינטואיציה של הפתרון הראשון.
אולי שכחתי בגלל שהתשובה היחידה שאני יכול לענות לשאלה זו היא "אינני יודע".
אני מעריך שיש לזה קשר לעובדה שכבר קודם לכך הבחנתי שלפעמים בניות עזר באמת מצדיקות את שמן ובאמת עוזרות.
בניית שריג בעל צלע שלמה על המלבן נראתה לי כבנייה עם פוטנציאל.
בניית השריג השני אולי התבצעה משיקולי סימטריה.
ואז – פתאום ראיתי את ההוכחה כולה.
המעניין הוא שהכל היה בראש – ללא שימוש בניר כלל.
זה קצת מזכיר את הסיפור על איש עשיר מאד שמישהו שואל אותו איך עשה את הונו והוא מספר את הסיפור הבא:
"הלכתי ברחוב וראיתי שני תפוחים מתגלגלים על הרצפה.
הרמתי אותם, הברקתי אותם, ומן הפדיון קניתי שלשה תפוחים.
גם אותם הברקתי ומכרתי וחוזר חלילה כך שבכל פעם היו לי יותר תפוחים…
ואז פתאום קראו לי מאיזה משרד עורכי דין ואמרו לי שאני קרובה היחיד של איזו מיליונרית שנפטרה…"
א.בן-נר ואהוד:
תודה על דבריכם.
היה לי ברור מראש שחלק מן האנשים לא יבינו. אני מאמין שזו לא בעיה של אינטליגנציה אלא בעיה של נכונות להשקיע כיוון שבאמת מדובר כאן בדברים שאולי קשה לגלות אבל לדעתי – כל אחד שמוכן להתאמץ יכול להבין.
אני מבסס את אמונתי בכך שכל אחד יכול להבין את הדברים על ניסיון רציני שרכשתי לפני שנים רבות בהעברת שעורים פרטיים.
הגיעו אלי תלמידים עם ממוצע ציונים 4-5 ובדרך כלל אחרי מספר מצומצם של שיעורים הם הגיעו לממוצע 9-10 כאשר עיקר המאמץ שהשקעתי בהם היה מופנה לשיקום ביטחונם העצמי ולחידוש אהבתם לנושא.
כן! חידוש! הרבה יותר קל למצוא זאטוט שאוהב מתמטיקה מאשר בוגר תיכון שאוהב מתמטיקה והסיבות לכך הן רבות.
אפשר להאשים את המורים ובוודאי שהם נושאים בחלק מן האשמה אבל הבעיה היא יותר של סביבה שיש בה שני מרכיבים הרסניים:
המרכיב האחד הוא שאנשים מתגאים (כן! לא יאומן, אבל הם מתגאים!) בחוסר יכולתם להתמודד עם בעיות מתמטיות (כמובן שזו רק התנהגות חיצונית אבל זו התנהגות מידבקת שמאומצת בקלות על ידי כל תלמיד שנתקל בבעיה כלשהי).
המרכיב השני הוא תכנית לימודים שאינה מדגישה את היופי של הדברים ואת ההנאה הרבה שניתן להפיק מהבנה מעמיקה של הדברים. זה מאד עצוב כאשר משווים את זה ליחס של אנשים לאמנות. משום מה אנשים מרגישים נוח להעריך אמנות גם אם אינם אמנים אבל בלימודי המתמטיקה יש מין אווירה תחרותית כזו שמתדלקת את התופעה שתיארתי כ"מרכיב הראשון" ובנוסף לכך יוצרת מצב שבו אנשים שאינם מתמטיקאים מלידה גם אינם יכולים להעריך את היופי שבדברים.
הנזק שבתחרותיות התחוור לי בגיל צעיר מאד.
תפקידו של אבי חייב את משפחתנו להעתיק את מקום מגורינו ממדינה למדינה פעמים רבות.
למעשה – למעט 4 השנים הראשונות של ביה"ס היסודי לא ביליתי יותר משנתיים באותו בית ספר.
זה דבר הרסני שפגע מאד בלימודים של אחי אבל אני תמיד נפלתי על הרגליים.
בבית הספר האחרון שבו הייתי (בית ספר בלגי בגרמניה) היה תלמיד שמהר מאד מצאתי אתו שפה משותפת כי גם הוא אהב מתמטיקה וחידות.
הבעיה הייתה שלא עבר זמן רב עד שגילה שאני עולה עליו ביכולותיי והתוצאה הייתה – מדהים ככל שזה יכול להישמע – שהוא הפסיק לאהוב מתמטיקה.
זה היה עבורי לקח חשוב אבל לא לקח שהפקתי מיד אלא כזה שהבנתי רק אחרי מספר שנים ואת הלקח הזה ניסיתי ליישם בהוראה הפרטית.
צריך לגרום לאנשים להיות מסוגלים לראות את היופי מבלי שזה יעורר בהם רגשי נחיתות (שבסוף מוצאים את ביטויים בהפגנת סלידה ממתמטיקה או בסרקאזם).
אני עדיין ממליץ לכל מי שלא התאמץ מספיק כדי להבין – לעשות מאמץ נוסף.
האמינו לי שזה שווה!
אהוד:
ביחס להערתך על התרשים – אינני רואה את התופעה שעליה אתה מדבר.
למעשה שלשת התרשימים של המלבן בהוכחה הראשונה נוצרו זה מזה (יצרתי את המלבן עם השריג השחור, אחר כך הנחתי על אותו מלבן את השריג האדום ואחר כך הנחתי על התוצאה את הטקסטורה שרואים בשלישי) ולכן הגיוני שקו שחסר בראשון יחסר גם בשני אבל במקרה כזה הוא צריך להיות חסר גם בשלישי.
מכל מקום – אינני רואה את החוסר עליו אתה מדבר וגם אינני רואה ריבועים בטור המלבנים (טור המלבנים הוא מכוון כי אורך הצלע אינו שלם ולכן המלבן אינו מתחלק לריבועים).
נראה לי כמו איזו בעיה בתצוגה של הדפדפן שלך אבל האמת שגם אילו רציתי לגרום לבעיה כזו לא הייתי יודע כיצד לעשות זאת כך שבעיני זו כרגע תעלומה.
אם אינני טועה אז באיור האמור להסביר את ההוכחה הראשונה חסר קו שחור המלבן הגדול מחולק לריבועים ואז פתאום מופיע טור של מלבנים המכילים בעצם זוג ריבועים . הקו השחור החסר גם אינו מופיע
באיור השני.
מיכאל
אני מוריד את הכובע. בהחלט הוכחות יפיפיות.
למרות שקשה לנסח אינטואיציה מתמטית מה גרם לך לחשוב על ההוכחה הראשונה? נראה כי הדרך ה"טבעית" להגיע להוכחה זו מקורה באינטגרציה דו-מימדית,אבל אתה ציינת כי על ההוכחה דרך האינטגרל הכפול שמעת רק מאוחר יותר.
לגבי אותם אנשים שחיפשו סיפור מסגרת לחידה הרי ניתן לחשוב על מהוד ללייזר. כדי שתיבה מסויימת
תהייה מהוד דרוש כי היא תהייה בעלת מימד השווה למספר שלם של חצאיי אורכי גל. ולכן ניתן לשאול
האם אפשר להרכיב תיבה או מלבן מאוסף מהודים מלבניים כך שלא יווצר מהוד?
לטעמי הבחירה בחידה הייתה רעיון מעולה כיון שאת היופי של המתמטיקה ניתן להציג בפשטות באופן גיאומטרי.כיוון שהדגמה כזו כמעט ואינה דורשת הסבר ידע או מושגים מוקדמים.
לכל המגיבים בסגנון :"אני אדם מן הישוב ולכן אני לא מבין מה כתוב"
או "המאמר קשה להבנה…בלה..בלה..בלה" ובכן רבותי,
אלף- אינכם חייבים לקרוא כל מאמר שמתפרסם.
בית- זה לא אסון לקרוא מאמר פעמיים או שלוש…להתאמץ..בסוף זה
יכול להשתלם.
כל זה בתנאי שזמנכם מאפשר לכם זאת .
ולמיכאל- תודה, מעניין להיזכר בלימודי באוניברסיטה לפני כ~30 שנה.
מיכאל,
ניסית להסביר.אז ניסית.ולמרות שאני מעריך זאת (!) יצא שהלכת למצוא מלוכה – ומצאת אתונות…
את יופיה של המתמטיקה לא ימצא הקורא ההדיוט ,ואללי – הוא אפילו ירגיש אידיוט.
נראה שאת היופי שבה יכולים רק פקוחי העיניים לראות,ומי שאין לו אותם קשרים אינטר-נוירליים מאד מסוימים במוחו ימשיך להעריץ את המתמטיקאים – אך הם ימשיכו להיות בעניו עופות מוזרים במדה זו או אחרת.
האם המסביר כשל – או אולי עפה המתמטיקה גבוה עוד ועוד ?
גם וגם.
ואני כאן למטה עם ההמון …
רון:
אינני משקיע בך.
ערן:
ב"חשיפת מתחזים" לא התכוונתי למישהו שמגיב כאן אלא לכל מיניאנשים שבכל מיני דיונים מנסים ללמד אותי לחשוב ואפילו ללמד אותי מתמטיקה (ומתחזים לכאלה שמבינים בעניין).
סימון סינג אולי ידוע כאשף בעניין אבל הוא לא מתמודד עם בעיות מתמטיות.
מכסימום הוא מציג תוצאות שלהן.
לא זה מה שניסיתי לעשות כאן.
אין לי בעייה עם הביקורת.
למיכאל:
מעניין אותי לדעת למה אתה מתכוון לחשוף מתחזים?
כמה דברים קטנים:
1. דבר ראשון, שאפו על העבודה הקשה, רואים את ההשקעה.
2. מה שהתכוונתי לומר זה שפשוט מעט מאוד אנשים יכולים להתחבר למאמר, מהסיבה הפשוטה שלכתוב מאמר מהסוג הזה שיהיה גם מעניין אנשים שלמדו (לפחות) את מקצועות הבסיס בתחום באוניברסיטה וגם שיהיה ברור להדיוטות הוא דבר מאוד מסובך ומעטים מסוגלים לו. לא סתם סיימון סינג נחשב עושה קסמים בתחום.
3. אנסה לקרא את המאמר שוב, הפעם עד סופו.
4. ביקורת מחזקת, לא?
כפי שאמרתי – פתרונות לשאלה זו (אותה פתרתי לפני כארבעים שנה (באמת!)) כבר התפרסמו וכיום אפשר למצוא חלק מהם באינטרנט.
למשל כאן:
http://www.inference.phy.cam.ac.uk/mackay/rectangles/
כאן:
http://www.helsinki.fi/filosofia/filo/jvp/coquand.pdf
כאן:
http://sbjoshi.wordpress.com/2008/07/31/rectangle-tiling-problem/
כאן:
http://mathdl.maa.org/images/upload_library/22/Ford/Wagon601-617.pdf
ובעוד הרבה מקומות אחרים.
נראה לי, עם זאת, שעל אף כל השנים שעברו, ההוכחה השלישית שתיארתי היא עדיין ייחודית – הן בפשטותה והן בכלי המחשבתי שהיא מנצלת.
מיכאל
אתה בתפקיד המורה אני בתפקיד התלמיד
רציתי להבין
אני אדם מהישוב ולא הבנתי כלום בטח שלא את החידה.
אולי חידה שקשורה למשהו פרקטי (אולי אפילו סיפורי) שאוכל לדמיין עדיפה
בתודה
חברים:
מכיוון שנקודה הציע מאמר על אינסופיות קבוצת המספרים הראשוניים, החלטתי להוסיף כאן פשוט תגובה המוכיחה זאת.
ההוכחה היא הוכחה פשוטה בדרך השלילה.
נניח שיש קבוצה סופית של ראשוניים שנקרא להם P1,P2,P3,……Pn
אם נסתכל על המספר P1xP2xP3x….xPn +1 הרי שמספר זה אינו מתחלק באף אחד מן הראשוניים הללו (כי תמיד נשארת שארית 1 בחלוקה) ולכן הוא חייב או להיות ראשוני נוסף בעצמו או להתחלק בראשוני נוסף שאינו מופיע בין הראשוניים הנ"ל.
במילים אחרות – הראינו שלכל קבוצה סופית של ראשוניים יש ראשוני אחד לפחות שאינו נמצא בה וזה מש"ל.
Jones:
המאמר כבר פורסם.
ניסיתי לנסח את השאלה באופן פשוט יותר בתגובות.
אני מניח שבסופו של דבר הבנת את השאלה כי אחרת לא יכולת להבין את ההוכחות (כי לא יכולת להבין מה מנסים להוכיח).
אינני יודע מהי בדיוק הנקודה של נקודה שאליה אתה מצטרף ובעיקר הייתי רוצה לדעת אם יש משהו שאתה מבקש ממני בהקשר זה.
כעיקרון – ידעתי מראש שזה מאמר קצת כבד בשביל אתר הידען (וגם אבי ורועי הזהירו אותי מפני נקודה זו מראש) אבל חשבתי שיש טעם לפרסם אותו עכשיו דווקא בגלל שתגובות שקראתי במאמרים שונים (בעיקר כאלה של לירן זיידמן) הראו לי שמשהו מסוג זה נחוץ לאנשים מסוימים (מן הסתם – לא אלה שהגיבו כאן – שאיש מהם גם לא הגיב על ניסוח השאלה אותה פרסמתי עוד לפני פרסום המאמר).
את ההוכחות הבנתי אבל לא את השאלה
אני מצטרף לנקודה של נקודה
עוד דבר לערן M:
בהחלט יכולתי לכתוב מאמר על נושא אחר וזה בוודאי היה יותר פשוט ואולי היו יותר קוראים.
יותר מכך – גם כתבתי מאמרים אחרים.
העניין הוא שאת התוכן של המאמר הזה לא ניתן להעביר בצורה לגמרי פשוטה וגם לא את התחושה של מה זה לפתור חידה מתמטית.
בדיונים כאן הצגתי פה ושם פתרונות לחידות מתמטיות פשוטות יותר.
הצגתי גם כמה חידות שאינן יותר פשוטות אבל לא הצגתי את פתרונן כי בניגוד לחידה זו – פתרונות שלהן לא התפרסמו בשום מקום וזה מאפשר לי להשתמש בהן לחשוף מתחזים.
אינני יודע איך אתה מגדיר אדם ש"נגיש למתמטיקה" אבל הרבה אנשים שבאמת "נגישים למתמטיקה" קראו גרסאות שונות של מאמר זה ואני חייב לומר שהתגובות של אנשים אלה היו ממש נלהבות.
העניין הוא, כמובן, שזה לא נועד למי שמתעצל לחשוב.
בוריס:
הזכרתי את ההוכחה הזאת במאמר אבל היא לא יותר פשוטה אלא הרבה הרבה יותר מורכבת.
בין השאר היא מצריכה לדעת לעשות אינטגרלים כפולים וגם אז זה לא לגמרי טריביאלי.
ערן M :
אתה אומר זאת למרות שאין במאמר אף נוסחה?
נקודה:
לא רציתי להביא דבר טריביאלי.
יכול להיות שהייתי צריך להסתפק בהוכחה השלישית שנראה לי שאיש מכם לא הגיע אליה למרות הזהרותיי.
יש את המשפט האומר שכל משוואה נוספת מורידה את כמות הקוראים הפוטנציאלים בחצי.
בתור אחד שדווקא נגיש למתמטיקה לא יכולתי לקרא את זה.
יש הוכחה הרבה יותר אלגנטית:
נקח אינטגרל כפול על
sin(2*pi*x)*sin(2*pi*y)dx*dy
על שטח כל המלבן.
אפשר להוכיח די בקלות שהאינטגרל מתאפס אם ורק אם לפחות אחת מצלעות המלבן שלמה (תרגיל!).
מכיוון שאינטגרל על מלבן שווה לסכום האינטגרלים על החלוקה שלו וכל אינטגרל בסכום מתאפס, האינטגרל על כל השטח מתאפס. מכאן נובע למלבן צלע שלמה. מש"ל
כמובן שאפשר להרחיב את ההוכחה לכל מימד.
המחשבה הראשונה שעלתה במוחי היא "מה זה הניסוח המעורפל הזה של החידה"
מחשבה שניה אומרת שאולי מתמטקאי שקורא את זה רואה משפט פשוט כמו x+x=2x
מסכים עם הנקודה של נקודה.
לאדם מן הישוב קשה לעקוב אחר המאמר.
דעתי היא שהחידה טכנית מידי ולא מראה את מה שניסית להראות…ובהחלט היה עדיף להשתמש באורך/רוחב. וגם מוסיף דוגמא שממחישה מה החידה שואלת.
אולי היה עדיף להביא משהו נקי ואלגנטי יותר, משהו כמו ההוכחה לכך שיש אינסוף מספרים ראשוניים. שמערב רק מימד אחד.
אולי אפשר לנסח כך:
נתון מלבן שמרוצף על ידי מלבנים פנימיים (לא בהכרח שווים).
נתון שבכל אחד מהמלבנים הפנימיים – האורך או הרוחב הם מספר שלם של סנטימטרים.
הוכח שגם במלבן החיצוני – האורך או הרוחב הם מספר שלם של סנטימטרים.
יש קצת בעיה עם הניסוח הזה כי מישהו עלול שלא להבין שזה נכון גם למילימטרים או לאינטשים ואולי הוא עלול גם שלא להבין שיש אפשרות שגם האורך וגם הרוחב יהיו בעלי מידה שלמה אבל יכול להיות שאפשר לוותר בעניינים אלה.
אגב:
אחת הסיבות לכך שפרסמתי את החידה קודם (במאמר על רמנוג'אן) הייתה לוודא שאנשים מבינים אותה.
היו שם שאלות והבהרות והנוסח הנוכחי מנסה לענות על הקשיים שהתעוררו שם.
באופן עקרוני הייתי רוצה להשתמש במונחים של "אורך" ו"רוחב" במקום "מימדים" אבל יש בעיה עם ביטויים כמו "האורך של האורך" או "האורך של הרוחב"
נקודה:
בסוף הבנת מה החידה?
יש לך הצעה לניסוח חלופי?
מיכאל שלום, תודה על המאמרים שאתה כותב, ועל המאמץ שאתה משקיע בהנחלת אהבת המדע והחשיבה הנכונה לכלל הקוראים החפצים לדעת בשביל הידיעה.
אני מעוניין לציין שכבר בהתחלה לא הרגשתי נוח עם הניסוח של החידה הראשונה, היא אולי מנוסחת בצורה מדוייקת, אך בודאי שהיא אינה מנוסחת בצורה בהירה לאדם מן הישוב שמנסה להבין מה בכלל החידה שואלת, וזה בדיוק מסוג הדברים שלדעתי מרחיקים אנשים מהמדע בכלל ומהמתימטיקה בפרט. והרי על זה בדיוק המאמר 🙂
תקן אותי אם אני טועה.