אי שוויון בל – לא מה שחשבתם

אי שוויון בל הוא אחד מהנושאים הכי מדוברים וגם הכי מבלבלים בקוונטים. כמעט כל פיזיקאי מכיר את המונח, אבל נתקלתי רק במעט שמבינים אותו לעומק. גם אני נחשפתי אליו בקורס מבוא, ורק שנים אחרי קלטתי עד כמה עקום הוא נלמד. אז החלטתי לעשות סדר – מה הוא מניח? מה נובע ממנו ובעיקר מה לא?

פיזיקאים נחשפים לראשונה למכניקת הקוונטים בשנה השנייה של התואר הראשון. לרוב, הקורס נפתח בציטוט של זוכה הנובל, פרופ׳ ריצ׳רד פיינמן- ״אם אתם חושבים שאתם מבינים את מכניקת הקוונטים, כנראה שאתם לא מבינים אותה״. המשפט המפורסם מתיימר להמחיש שמכניקת הקוונטים לא אינטואיטיבית וכדי להבין את הטבע צריך לעקוב אחר המתמטיקה, ולא אחר תחושת הבטן. אינטואיציה הרי נבנית על סמך חיי היום יום, המבוססת ברובה על המכניקה הקלאסית. מכניקת הקוונטים, לעומת זאת, שונה מהותית מהפיזיקה הקלאסית ולכן האינטואיציה האנושית יכולה להטעות.

בדרך כלל, כבונוס בסוף הקורס, המרצה מספר על אי-שוויון בל המפורסם, שלכאורה מעיד שמכניקת הקוונטים היא תאוריה לא-לוקאלית, כלומר שחלקיקים יכולים להשפיע זה על זה באופן מיידי, מהר יותר ממהירות האור. לעיתים המרצה מתבל את ההרצאה באגדה הידועה שאיינשטיין ניסה להיפטר מהמוזרויות של מכניקת הקוונטים באמצעות ההנחה שלחלקיקים קיימים ״משתנים חבויים״ – כלומר, תכונות פיזיקליות שלנסיין אין גישה אליהן, או שהוא כלל לא מודע לקיומן, אך משפיעות על תוצאות הניסוי. ואז, כדרך אגב, המרצה מציין שאי-שוויון בל מוכיח שמשתנים חבויים אינם יכולים להתקיים, ושאיינשטיין טעה.

כששמעתי את הטענה הזו לראשונה, קיבלתי אותה כעובדה. הרי אמרו לי, במכניקת הקוונטים אין אינטואיציה, תעקוב אחר המתמטיקה. פיינמן גם נהג לומר "Shut up and calculate" (סתום את הפה ותחשב), כלומר אל תבלבל את המוח, פשוט תחשב ותאמין למה שאתה מקבל. מי אני לעומת פיינמן? גדולים ממני חישבו דברים וקיבלו תוצאות, לא נאמין להם?

אחרי יותר מעשור בפיזיקה, אני מאמין אחרת. אנחנו יכולים לרכוש אינטואיציה על העולם הקוונטי. ככל שנחשפים יותר למתמטיקה ולפיזיקה, המוח האנושי מסוגל לתפוס את הפיזיקה החדשה ולרכוש אינטואיציה עליה. הסיבה שאני מאמין בטענה זו היא שאם זו לא הייתה נכונה, מכניקת הקוונטים לא הייתה ממשיכה להתפתח ופיזיקאים לא היו מגלים דברים חדשים. לשם כך נדרשת יצירתיות, תחושת בטן וקפיצות מחשבתיות שבלעדיהן לא היו מתגלות תופעות חדשות.

לצערי, בגלל תפיסה מוטעית על מכניקת הקוונטים, או עצלנות דידקטית, מרצים מלמדים טעויות, או חלקי אמת, כי כך הם חונכו. אי שוויון בל היא דוגמה מצוינת לכך: לכאורה טענה שמלמדת אותנו רבות על מכניקת הקוונטים, שנבדקה במספר ניסויים וזיכתה חוקרים בפרס נובל, אך רבים מהפיזיקאים פשוט לא באמת יודעים על מה היא מבוססת, מה היא באמת אומרת ומה לא. הייתי צריך ללמוד את זה בעצמי, כדי להבין עד כמה לא ידעתי, ועד כמה החור האקדמי מחלחל לקהל הרחב, שמסיק על מכניקת הקוונטים טעויות או כוחות על.

בפוסט הזה אשתדל להסביר את ההנחות של אי שוויון בל והמסקנות שנובעות ממנו עם קצת מתמטיקה. אני חושב שכך המסר יעבור בצורה מדויקת יותר, אבל מי שאינו בקיא בהסתברות יכול להתמקד בטענות הכתובות בטקסט. אני מקווה שגם בלי המתמטיקה התוכן יועבר בבירור.

ניסוי מחשבתי

את אי שוויון בל אפשר להסביר איכותנית בעזרת ניסוי מחשבתי. נדמיין לעצמנו שני נסיינים – אליס ובוב – שמבצעים מדידה סימולטנית על שני מערכות פיזיקאליות מופרדות. פרטי הניסוי עצמו פחות חשובים, אך מה שכן רלוונטי לדיון הוא שכל נסיין יכול למדוד שתי תוצאות אפשריות – 0 או 1. התוצאה הבינארית מייצגת תבנית פיזיקאלית שמודדים, למשל אור פגע בגלאי הראשון או בשני, הקיטוב של האור מאונך או מאוזן, זה לא משנה מה התבנית, העיקר שקיימות שתי אפשרויות שונות ומובחנות. כמובן שלא תמיד מערכת הניסוי תלויה במשתנים בינאריים, זווית הקיטוב למשל היא פרמטר רציף, אך כל עוד ניתן לבצע ״דיסקרטיזציה״, כלומר לייצג טווח תוצאות מסוים כ-0 ואת השאר כ-1, מבחינתנו הניסוי מקביל למדידה בינארית. כמובן שלא תמיד נקבל בהכרח את אחת מהתוצאות. למשל, פוטון יכול לברוח ממסלולו, או שלעיתים נמדוד כמה פוטונים בו זמנית. גם כאן ניתן לעגל פינות ולהכליל מקרים אלו למשל לקבוצה 1. כל עוד הגדרת מראש ובמפורש את כללי המשחק, ודאגת שבכל סיטואציה נקבל את אחת מבין האפשרויות, הניסוי כביל.

מרגע שכללי המשחק נקבעו, הניסוי מתחיל. כאן, אליס ובוב מודדים את ההסתברות P(a,b|x,y). זו הסתברות מותנית, כלומר הסתברות התלויה בקלט הניסוי. בהנחה שהקלט הוא x,y, כאשר x הוא הקלט של אליס ו-y הוא הקלט של בוב, מה ההסתברות שתוצאת הניסוי היא a עבור אליס ו-b עבור בוב? הקלט מאתחל את מערכת הניסוי של אליס ובוב והוא יכול להיות מתואר בעזרת שרשרת של ביטים, כלומר אפסים ואחדים, כנ״ל לגבי הפרמטרים a,b. בניסוי זה, סביר להניח שלאליס ובוב אין שליטה מלאה על המערכת הקוונטית, לכן כל מה שנוכל לעשות הוא לשער את ההסתברות הנמדדת. בהנחה שהמערכת הקוונטית מתוארת על ידי אוסף פרמטרים שנסמן באות למדא

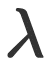
אזי ההסתברות שנמדוד כעת תהיה הממוצע על כל המצבים האפשריים.

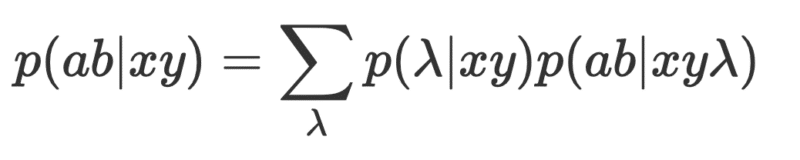
נזכיר, האות למדא מייצגת אוסף של מספרים המתארים את המצב הקוונטי של בוב ושל אליס אך לא תמיד הם יודעים במלואם. את למדא איינשטיין כינה ״משתנים חבויים״, כי אלו לא תמיד גלויים לנסיין או לא תמיד נתונים לשליטתו. האיבר הראשון בסכום מתאר את ההסתברות שהמערכת הקוונטית נמצאת במצב למדא בהנחה שכיילנו את מערכת הניסוי עם הקלטים x,y. שימו לב שביטוי זה מגדיר זהות מתמטית ולא הנחה כלשהי.

כעת מגיעות ההנחות. ההנחה הראשונה היא שהמערכת הפיזיקאלית המתוארת על ידי למדא לא תלויה בקלט x,y. כלומר

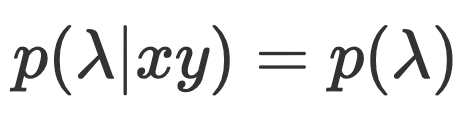
אני מאמין שזו הנחה סבירה בהחלט. הציפייה הטבעית היא שהמערכת הפיזיקאלית שעליה אנחנו מבצעים את הניסוי ומכינים מראש לא תלויה בכיול כלי המדידה.  לא בכדי הנחה זו מכונה ״אין קונספירציה״, כי אם הייתה כזו, לא היינו יכולים לבחון את טבעה האמיתי של המערכת הפיזיקאלית. באנלוגיה לכך, זה כמו שחברת טבק תבחר את הנסיינים שלה לניסוי שבוחן את הקשר בין סרטן לעישון. לעיתים ההנחה מכונה כהנחת ״חופש הבחירה״ או ״אין סופר-דטרמיניזם״. כעת, מהנחה זו נקבל,

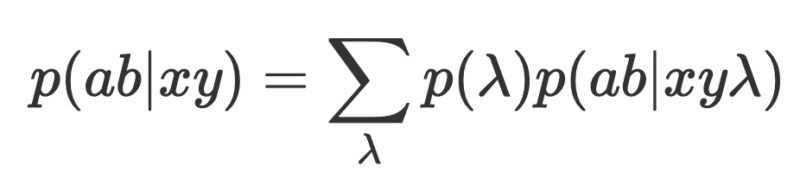
הסברה השנייה מניחה שהגדלים המדידים a,b הם פונקציות דטרמיניסטיות של הקלטים x,y ושל המשתנים החבוים. סברה זו יחסית הגיונית. היא מניחה שאם נדע את למדא לחלוטין, נוכל בעזרתה ויחד עם הקלטים x,y לנבא במדויק את תוצאות הניסוי. במילים אחרות ההסתברות

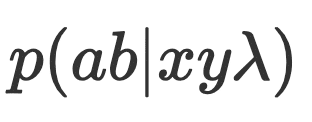
חייבת להיות שווה לאפס או אחד, כי ההסתברות קורסת והופכת למיותרת אם הכל ברור וידוע. מסקנה מיידית מהנחת הדטרמיניסטיות היא

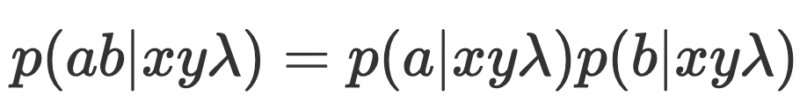
משום שהקלט מגדיר לבדו את תוצאות הניסוי של בוב ואליס בנפרד. לעיתים עיקרון זה מכונה ״ריאליזם״. דטרמיניסטיות וחופש בחירה ביחד נותנים

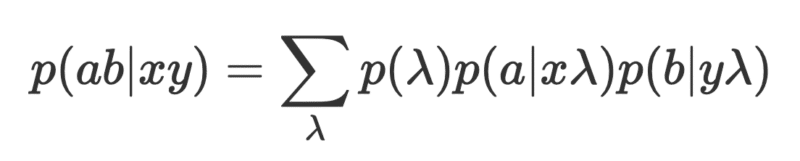
ההנחה האחרונה שנעזר בה היא שתוצאות הניסוי של אליס לא תלויות באיך שבוב מכין את הניסוי, כלומר ב-y והפוך באופן זהה. הסיבה לכך היא שמשום ששני הניסויים נערכים סימולטנית הרחק אחד מהשני, לא ניתן לצפות שהקלט שמאתחל את הניסוי של בוב יכול להשפיע על מה שאליס תקבל (ונכון גם עבור איך שאליס מכינה את הניסוי שלה ביחס למה שבוב מודד):

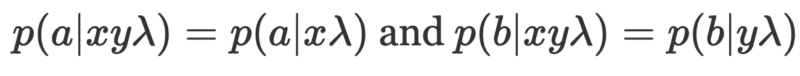
הנחה זו מכונה כ"אין פעולה ממרחק״ . לסיכום, ההסתברות למדוד a,b בניסוי של בוב ואליס, בהנחה שמערכות הניסוי כוילו בהתאם לקלטים x,y וקיימים משתנים חבויים שאין לנו שליטה עליהם, מוגדרת באופן הבא:

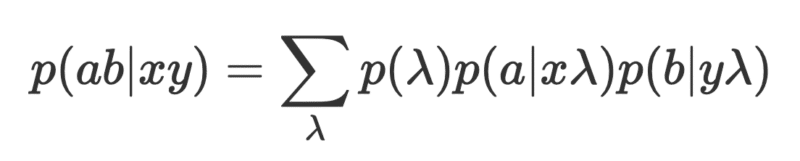
כעת אנחנו במקום שניתן לנסח את אי שיוויון בל.

נניח ואליס ובוב משחקים משחק שניצחון בו מוגדר מראש ותלוי ביחסים בין הקלט והפלט. למשל, אם אליס ובוב מכוונים את מערכת הניסוי שלהם עם הקלטים (0,0), (0,1), (1,0) אזי ניצחון יחשב אם הפלט של אליס ובוב זהה ואם הקלט הוא (1,1) ניצחון יחשב אם הפלט של אליס ובוב שונה. להזכירכם, זהו משחק הסתברותי, לכן אפשר לחשב את ההסתברות לניצחון. אם מניחים דטרמיניזם, שאין קונספירציות ואין אינטראקציות מיידיות במרחק, מקבלים את אי שוויון קלאוזנר-הורן-שימוני-הולט, כלומר מה הגודל המקסימלי שההסתברות הצלחה יכולה להיות. מצד שני, מתוך מכניקת הקוונטים מקבלים אי שיוון חדש המכונה אי שוויון בל. ואכן, ניסוים הראו שאכן ניתן לעקוף את הגבול הקלאסי העליון ולהיות בתחום הקוונטי. אם כך, אחת מההנחות שתיארנו בתחילת הכתבה איננה נכונה. אך מי מהן?

סופר-דטרמיניזם או יקום לא לוקאלי?

במכניקת הקוונטים הכל הסתברותי, אז למה שלא פשוט נוותר על דטרמיניזם וזהו?

כל עוד דטרמיניזם מתקיים, האופי ההסתברותי של מכניקת הקוונטים מתבטא בחוסר הידע של הנסיין על מערכת הניסוי (הנובע מהמידע החלקי שיש לנסיין ונמצא במשתנים החבויים). לעומת זאת, אפשר להניח שהיקום לא דטרמיניסטי ותוצאות הניסוי הן הסתברותיות לחלוטין. במקרה הזה, האופי ההסתברותי של מכניקת הקוונטים הוא יסודי ואין הכרח במשתנים חבויים. אז האם כדאי לוותר על דטרמיניזם ולהניח שהיקום מתנהל הסתברותית? אם מוותרים על דטרמיניזם, האיסור על פעולה ממרחק נשמר אך על הדרך מוותרים על תכונה חשובה אחרת: לוקאליות-קוזאלית.

לוקאליות קוזאלית מגדירה ששני מאורעות המתרחשים מחוץ ל״קונוס האור״ לא משפיעים אחד על השני במיידית. קונוס האור הוא קונספט פיזיקאלי שמגדיר קוזאליות, ובתוכו כל המאורעות בזמן ובמרחב שמהם יכול להשלח מידע אל מערכת הניסוי לפני שזו מתרחשת. אם הם מאורעות ״דמויי מרחב״ המאורעות עצמם נמצאות מחוץ לקונוס האור אחד של השני ואין השפעה ישירה בניהם. מבלי להיכנס לאלגברה, השילוב של דטרמיניזם יחד עם האיסור של פעולה ממרחק נותנים את אותו תנאי הסתברותי שתופעה מחוץ לקונוס האור של הניסוי לא משפיעה עליה. לפיכך, ניתן להחליף את ההנחות הקודמות בלוקאליות-קוזאלית ובאיסור הקונספירציה.

אז אם מוותרים על הדטרמיניזם, לוקאליות ביקום נעלמת. לכך פיזיקאים מתכוונים כשהם אומרים שמכניקת הקוונטים לא לוקאלית. שימו לב שלוקאליות נשברת רק עבור המשתנים הגלויים, בעוד שעל המשתנים החבויים לא הנחנו דבר (הם יכולים להיות לוקאלים או לא). היום, מקובל לטעון שלוקאליות קוזאלית נשברת ולא רק דטרמיניזם. יחד עם זאת, אפשר לוותר על דטרמיניזם מבלי לוותר על איסור פעולה מרחוק.

אבל אין באמת סיבה לוותר דווקא על דטרמיניזם. אפשר לוותר על האיסור על הפעולה מרחוק ולאפשר את קיומם של משתנים חבויים (או לא, זה נתון כבר לבחירתך). לכן יש להיזהר מטענות נפוצות שלפיהן אם מכניקת הקוונטים אינה לוקאלית, הדבר גורס בהכרח שאין משתנים חבויים, וגם שפעולה ממרחק אפשרית. מדובר בשני תנאים נפרדים.

למען האמת, אין סיבה לוותר על לוקאליות דווקא ולא לאפשר קונספירציה במקום. אפילו בל בעצמו חשב אחרת. בראיון ל-BBC, בל אמר: ״ניתן לעקוף את הבעיות הנובעות כביכול מתופעות הדורשות מהירות הגבוהה ממהירות האור או מפעולה המתרחשת במיידית במרחקים, אך היא דורשת דטרמיניסטיות מוחלטת ביקום, כזו שמבטלת את הבחירה החופשית. דמיינו יקום סופרטרמיניסטי שמכיל לא רק טבע דומם הפועל כשעון מאוחרי הקלעים, אלא גם את הבחירות שלנו, אילו ניסוים נבצע ואת מה נמדוד. כולם נקבעו מראש. אין צורך בשיגור אות במהירות הגבוהה ממהירות האור כדי לספר לחלקיק א׳ איזה ניסוי בוצע בחלקיק ב׳ משום שהיקום, כולל חלקיק א׳ יודעים מראש איזו מדידה בוצעה ואת תוצאתה״.

כלומר, אם מתעקשים, לאפשר קונספירציה ולשמור על לוקאליות. העולם הסופר-דטרמיניסטי מעולם לא הופכך, ובשנים האחרונות הפופולאריות שלו גברה. זה נכון שאם הכל נקבע מראש המדע קצת מאבד משמעות אך אי אפשר לפסול את האפשרות הזו מראש על סמך אי שוויון בל.

אז האם מכניקת הקוונטים באמת לא לוקאלית? או שהכל ידוע מראש? כנראה שעוד מוקדם לדעת.

הכתבה ברובה התבססה על הבלוג הזה

לאלו המתעניינים בהסבר מתמטי מעמיק יותר מוזמנים לקרוא את הכתבה המלאה בבלוג שלי ״למה הקוונטה״. יש לכם שאלה? רוצים שאכתוב על נושא שמעניין אתכם? פנו אליי לכתובת המייל: [email protected]
אתם מוזמנים גם לעקוב אחרי גם ב-BlueSky כדי להתעדכן על הרצאות לקהל הרחב.

עוד בנושא באתר הידען:

• פילוסופיה של הקוונטים חלק ב'. הפרדוקס של אשר פרס: האם העתיד גורם לעבר?
• Beam me up Scotty:אבל רק עבור חלקיקים קוונטיים
• סודות שמורים היטב. ההצפנה הקוונטית מהתיאוריה למעבדה, ולמוצרים
• לווינים על הכוונת