פריצת דרך בגרפיקה ממוחשבת: אלגוריתם לכיווץ יעיל של גופים תלת מימדיים

שלושה חוקרים פרסמו מאמר בו הם מתארים אלגוריתם יעיל לכיווץ אובייקטים תלת מימדיים. האלגוריתם מהווה פריצת דרך בתחום התלת מימד, ובתקווה הוא יקל על העברת תמונות תלת מימדיות ברשת והשימוש בהן

ינון קוסטיקה

קישור ישיר לדף זה: https://www.hayadan.org.il/algoritm240604.html

שלושה חוקרים פרסמו מאמר הנקרא "Variational Shape Approximation" בו הם מתארים אלגוריתם חדש לכיווץ יעיל של אובייקטים תלת מימדיים. גרפיקה תלת מימדית נמצאת בשימוש בתחומי המסחר האלקטרוני, האנימציה הממוחשבת, הבידור באינטרנט ועוד.
עד היום נמצאו שיטות יעילות יחסית לכיווץ קול, תמונה ווידאו, אך לגרפיקה תלת מימדית לא נמצאה שיטת כיווץ יעילה. יתרה מכך – בעוד שבתחום אותות הקול והתמונה ניתן היה להשתמש בכלים מתמטיים דוגמת טרנספורם פורייה על מנת להעריך עד כמה הכיווץ קרוב לאופטימום, בתחום כיווץ התלת מימד לא קיימים כלים מספיק מפותחים על מנת לעשות כן. המאמר שפורסם מניח יסודות מתמטיים לכך, ומציע אלגוריתם כיווץ הנשען על גישה שונה מזו שננקטה עד כה.
שלושת החוקרים, דוד כהן שטיינר מאוניברסיטת דיוק (Duke) שבצפון קרוליינה, פייר אליאז (Pierre Alliez) מ-INRIA שבצרפת, ומת'יו דסברון (Mathieu Desbrun) מאוניברסיטת דרום קליפורניה (USC) יציגו את המאמר ואת ביצועי האלגוריתם המתואר בו בכנס הגרפיקה השנתי SIGGRAPH שייערך באוגוסט השנה בלוס-אנג'לס.
מודלים תלת מימדיים בגרפיקה ממוחשבת נמצאים כיום בשימוש נרחב, ההולך וגובר עם צמיחת תחומי המסחר האלקטרוני והבידור באינטרנט. חנויות וירטואליות מעונינות להציג באתרן תמונות תלת מימדיות של כל המוצרים המוצעים למכירה, מוזיאונים מעונינים לפרסם מוצגים שאינם דו מימדים דוגמת פסלים, גילופים, אגרטלים, תעשיית הסרטים המצויירים התלת מימדיים דוגמת "צעצוע של סיפור" מתרחבת ועוד. שיטת כיווץ יעילה לאובייקטים תלת מימדיים תקל מאוד על העברתם בקנה מידה רחב, ולכן תהיה מאוד אטרקטיבית ושימושית לתחומים אלו.
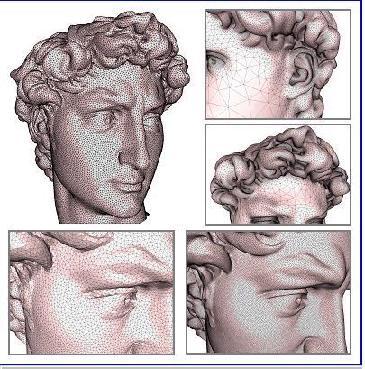
עד היום ייצוג של אובייקטים תלת מימדיים נעשה באמצעות חלוקה של האובייקט למשולשים במרחב בעלי קודקודים משותפים. חלוקה זו יצרה רשת של משולשים (Mesh) המייצגת את האובייקט. הייצוג היה יקר ביותר, ואף ייצוג של מישור דרש לעיתים מספר רב של משולשים, שרובם מיותרים ומסבכים את הייצוג.
מעבר ליתירות המשולשים, הוכח כי מציאת חלוקה אופטימלית של אובייקט תלת מימדי למשולשים היא בעיה NP-קשה, כלומר לא קיים אלגוריתם כללי המספק פיתרון מעשי לבעיה מבחינת זמן הריצה. מסיבה זו עיקר העיסוק בייצוג תלת מימד בשנים האחרונות התרכז במציאת חלוקות כמעט-אופטימליות בזמן ריצה מעשי (פולינומיאלי לכל היותר).
החידוש שהציגו שלושת החוקרים נבע מהגישה לפיתרון: במקום למצוא אלגוריתם חלוקה למשולשים, הם השתמשו בשיטות קיימות וניסו לצמצם את מספר המשולשים בפיתרון. כלומר במקום להשתמש בייצוג כפי שהוא, האלגוריתם שהציעו השלושה מנסה לפשט תוצרים של חלוקות לא-אופטימליות. את הפישוט מבצע האלגוריתם על ידי איחוד מספר גדול ככל הניתן של משולשים לאלמנט גיאומטרי גדול מבלי לפגום משמעותית באיכות התמונה הנשמרת. התוצאה המתקבלת היא אלגוריתם המייצג למשל מישור באמצעות מצולע גיאומטרי יחיד, ולא באמצעות קבוצה גדולה של משולשים. משטחים עקומים דורשים כמות גדולה יותר של מצולעים, אולם מספרם הכולל של המצולעים הנדרשים לייצוג בשיטה זו קטן בסדר גודל ממספר המשולשים הנדרשים לייצוג אותו משטח באלגוריתמים סטנדרטיים הקיימים כיום.

האלגוריתם משתמש באלגוריתם החלוקה של לויד (Lloyds Clustering Algorithm) שהוא אלגוריתם דטרמיניסטי המשתמש בניסיונות איטרטיביים על מנת למצוא חלוקה אופטימלית של קבוצת נקודות ל-k אזורים, כאשר k נקבע מראש. הרעיון של אלגוריתם זה פשוט: תחילה נקבעות k נקודות אקראיות שמתפקדות כמרכזם של האזורים. לאחר קביעת המרכזים משייכים כל נקודה מקבוצת הנקודות למרכז הקרוב ביותר אליה. כך למעשה נוצרות k קבוצות זרות של נקודות. בשלב הבא מחשבים עבור כל קבוצה כזו את המרכז הממוצע (Centroids), כלומר הנקודה שסכום המרחקים ממנה אל שאר הנקודות הוא הקטן ביותר. לאחר שמצאנו את k המרכזים החדשים חוזרים על התהליך שוב ושוב – כלומר מגדירים את הקבוצות של הנקודות הקרובות ביותר, מחשבים את המרכזים החדשים וכן הלאה, עד שמתמלא איזשהו תנאי עצירה מוגדר מראש.

באלגוריתם המוצג במאמר משתמשים באלגוריתם החלוקה של לויד בשינוי קל על מנת לחלק את האובייקט התלת מימדי לאזורים שונים שאינם נחתכים זה בזה. במקום למצוא מרכזים של קבוצת נקודות, מחשבים באלגוריתם נקודה מייצגת לכל אזור (הנקראת Geometric Proxy). לאחר חישוב הנקודות המייצגות מבוצע שלב הכיווץ, בו מאחדים אזורים לאזורים גדולים יותר, על מנת להקטין את כמות המידע המייצגת את האובייקט. ההחלטה האם לבצע את האיחוד של שני אזורים תלויה בשיעור איבוד המידע, כלומר אם יאבד מידע רב מדי שיפגום באיכות התמונה לאחר מכן מעבר לערך שהוגדר מראש אזי לא יבוצע האיחוד (לתכונה זו של האלגוריתם קוראים Error-Driven). מבצעים את תהליך הכיווץ מספר פעמים עד שלא ניתן לאחד יותר אזורים מבלי לפגום באיכות התוצר, ואז יוצרים מהאזורים שנותרו רשת (Mesh) של מצולעים. השינוי המוצג בחלק זה הוא שבעוד שבעבר הייצוג היה על ידי משולשים בלבד הייצוג כאן גם משלב מצולעים בעלי מספר גדול יותר של צלעות.

התוצאה המתקבלת היא חלוקה של האובייקט לרשת של מצולעים המייצגים את האובייקט בצורה יעילה הרבה יותר מכפי שניתן היה להשיג עד כה. מרשת המצולעים הזו ניתן ליצור ולהציג את האובייקט התלת מימדי המקורי על המסך.

מומחה בתחום, פרופסור ג'רר מדיוני (Medioni), אומר כי זהו אינו אלתור אלא חידוש עם יסודות פורמליים חזקים. אמנם ניתן ליצור מקרי קצה אותם האלגוריתם לא יצליח לכווץ, אולם עבור כל האובייקטים הרגילים האלגוריתם מניב תוצאות מעולות.

דסברון מסכם ואומר כי הוא מאמין שגישה זו מציעה גם יסודות מתמטיים חזקים וגם ביצועים חסרי תקדים. "בשילוב מספר פריצות דרך נוספות שנעשו לאחרונה בתחום כיווץ רשתות מצולעים (Mesh) זהו צעד משמעותי להקלת השימוש באובייקטים תלת מימדיים בתחומים רבים".

קישורים:
אתר הבית של פייר אליאז (בו מופיע המאמר):
אתר הבית של SIGGRAPH
ידען המתמטיקה

https://www.hayadan.org.il/BuildaGate4/general2/data_card.php?Cat=~~~880144455~~~65&SiteName=hayadan