אדולף קטלה האמין שהוא מסוגל להכניס את בני האדם לתוך אותה מסגרת נוקשה שהציבה הסטטיסטיקה. “המקריות,” טען קטלה, “היא רק צעיף המכסה על בערותינו.”
עבור רובנו, האנשים שמכירים את המספרים והמשוואות רק משיעורים משעממים בבית הספר, כל הנושא הזה נראה טכני, משעמם ומייגע- אבל כל מתמטיקאי יגיד לכם שמתמטיקה היא יפה. יש בה אלגנטיות מדהימה שנחשפת בעיקר כשאתה מגלה עד כמה היא מסוגלת לקשור יחדיו תופעות טבע שנראות, על פניו, בלתי קשורות לחלוטין זו לזו. הסיפור הבא ידגים את האלגנטיות הזו.
אדולף-ז’אק קטלה (Quetelet) נולד בעיר הבלגית גנט בשנת 1796. הוא היה איש אשכולות של ממש: כתב שירה, חיבר מחזות, תרגם ספרים וגם לימד מתמטיקה, פיסיקה ואסטרונומיה. הוא היה מדען מוצלח, והראשון שקיבל את התואר ‘דוקטור למדעים’ מאוניברסיטת גנט.
ב-1823 נשלח קטלה לפריז. המטרה המקורית של הביקור הייתה התמחות באסטרונומיה, אך בצרפת פגש קטלה את אחד מהמתמטיקאים הגדולים של דורו- פייר סימון לפלאס. זו הייתה פגישה גורלית עבור קטלה, שכן לפלאס הצית אצלו אהבה גדולה לסטטיסטיקה.
הסטטיסטיקה הייתה תחום צעיר ולא מפותח באותם הימים, אבל המתמטיקאים שעסקו בנושא זה כבר הספיקו לגלות כמה עובדות מסקרנות.
נניח, למשל, שאנחנו מודדים את הטמפרטורה של דלי מים רותחים באמצעות מד חום. מד החום איננו מושלם ולכן בכל פעם שנכניס אותו לתוך הדלי, נקבל תוצאה שונה. השינויים יהיו זעירים- שברירי מעלה לכאן או לכאן: במדידה אחת נקרא 100.5 מעלות, במדידה הבאה אולי 99.5 מעלות.
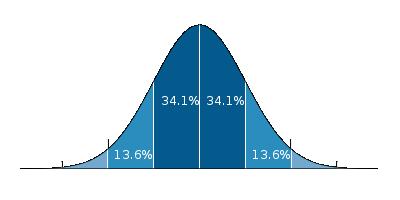
כדי להיות בטוחים בתוצאת המדידה שלנו, נבצע אלף מדידות שונות ונרשום את התוצאות בגרף: הציר האופקי בגרף יהיה הטמפרטורה הנמדדת והציר האנכי- כמה פעמים קיבלנו את אותה המדידה.
הגרף שנקבל יהיה בצורת פעמון: אזור מרכזי גבוה ושוליים שהולכים וקטנים בהדרגה. יהיו המון מדידות שנעות סביב נקודת מאה המעלות, ומעט מדידות שהולכות ומתרחקות ממנה- למשל, עשר מדידות של 101 מעלות, 5 מדידות של 102 מעלות ורק 3 מדידות של 104 מעלות.
המתמטיקאים נתקלו בגרף הפעמון הזה בהמון ניסויים שונים בפיסיקה. כמעט בכל פעם שמדידה חזרה על עצמה שוב ושוב, למשל- מדידת מהירות, זרם חשמלי, אורך, רוחב ומה לא- התוצאה הייתה עקומה של פעמון. למעשה, כל כך הרבה ניסויים ומדידות הפיקו את אותה צורת פעמון עד שהיא קיבלה את השם ‘התפלגות נורמאלית’: כך מתנהג הטבע באופן נורמלי.
אבל פיסיקה זה דבר אחד, ובני אדם זה משהו אחר. אנחנו לא דלי מים בעל טמפרטורה אחת- אנחנו שונים זה מזה. כל אחד מאיתנו נראה אחרת: גבוה, נמוך, רזה, שמן, קירח, שעיר ועוד ועוד. ההבדלים בין בני האדם, כך נדמה, הם אקראיים לחלוטין.
אדולף קטלה האמין שהוא מסוגל להכניס את בני האדם לתוך אותה מסגרת נוקשה שהציבה הסטטיסטיקה. “המקריות,” טען קטלה, “היא רק צעיף המכסה על בערותינו.”
כדי להוכיח את דבריו, קטלה מדד את גובהם של מאה אלף טירונים בצבא הצרפתי, וצייר את התוצאות על גרף. גובהם של רוב החיילים נע סביב איזה שהוא ערך מסוים- למשל, מטר ושבעים ס”מ- וככל שמתרחקים מאותו ערך מספר החיילים יורד. רק חלק קטן מהם מתנשא לגובה של מטר ותשעים או מטר וחמישים. אם התיאור הזה מוכר לכם, אתם צודקים: לגרף שקיבל קטלה היה צורה של…פעמון.
מכאן, שגם הגובה האנושי מציית לאותה התפלגות סטטיסטית ‘נורמאלית’ של מדידות טמפרטורה. קטלה מצא סדר מסוים בתכונה אנושית שעל פניו היא אקראית לחלוטין. קטלה מדד גם את היקף החזה של ששת אלפים חיילים סקוטיים, ושוב קיבל את אותה ההתפלגות הנורמאלית.
מנין הקשר שבין התנהגותו של מד-חום בתוך דלי מים רותחים, לגובה של חיילים צרפתים? על פניו, אלו תופעות שונות לחלוטין. קטלה ניסה לפתור את הדילמה הזו באמצעות הסבר מקורי: הוא טען שהטבע מנסה ליצור בן אדם (במקרה הזה, חייל צרפתי) בעל גובה ‘אידיאלי’. אבל הטבע מפספס. במקום חייל בגובה האידיאלי, הוא מייצר חייל ‘שגוי’, בגובה שונה מהרצוי. הצטברות השגיאות הללו יוצרת את עקומת הפעמון, אותה עקומת פעמון שיוצרות גם שגיאות מדידת הטמפרטורה בדלי.
בעיניים מודרניות, קל לראות שקטלה טועה לחלוטין. הטבע לא מנסה ‘ליצור’ שום דבר, ואם כבר היה מנסה ליצור משהו מושלם- זה בטח לא יכול להיות חייל צרפתי.
כדי לסבך את העניינים עוד יותר, קטלה החליט למדוד דברים שונים לחלוטין. למשל, את שיעור ההתאבדויות בעיר מסויימת, או את חומרת הפשיעה לפי שנה, או התפלגות גיל הנישואים. גם שם, הוא גילה, הגרף נראה בדיוק אותו הדבר: התפלגות נורמלית.
המשמעות של הממצא הזה היא לא פחות ממדהימה. אותו חוק מתמטי, אותה ‘משוואה’ אם תרצו, שמתארת תופעות בעולם הפיסיקה והאסטרונומיה- מתארת גם תופעות שהן לחלוטין לא פיסיקליות, כמו גיל הנישואים בבלגיה ובצרפת. ישנו קשר עמוק וחבוי בין שני תחומים שנראים על פניו שונים לחלוטין, והקשר הזה הוא מתמטי. מהי משמעותו של ממצא זה- ורבים כמותו- על תפיסת העולם שלנו? האם המתמטיקה היא סוג של בד עליו מצוירת המציאות שלנו, בד אשר משמש כרקע משותף לכל תופעה שניתקל בה? זו שאלה שמרתקת את הפילוסופים של המתמטיקה כבר אלפי שנים, וכנראה תמשיך לעשות כן גם בעתיד הנראה לעין.
[סיפורו של קטלה לקוח מתוך הספר ‘האם אלוהים הוא מתמטיקאי’, מאת מריו ליביו. רן לוי הוא סופר מדע פופלארי ומגיש את הפודקאסט ‘עושים היסטוריה!’ על מדע, טכנולוגיה והיסטוריה. www.ranlevi.co.il]

41 תגובות
ברצוני להוכיח שההתפלגות הנורמאלית היא גנטית. יש עוד תופעות חוץ מתופעת המדחום המערערות החלטה זו?
ר.ח:
פשוט נראה לי בלתי סביר שגובה האנשים הוא סכום (או ממוצע) של המון משתנים בלתי תלויים ושווי התפלגות.
מה גם שהטענה אינה רק לגבי גובה אלא לגבי כמעט כל דבר וגובה היה רק דוגמה.
האם ייתכן שכמעט כל דבר הוא סכום של משתנים בלתי תלויים ושווי התפלגות?
מכ*אל,
אתה מדגים כאן יפה את המנגנון לטענה שלי שתופעה המורכבת ממספר פרמטרים לא תלויים תראה הרבה פעמים התפלגות נורמלית אפילו אם לכל פרמטר יש רק שני ערכים (כמו בדוגמא שלך מטר ושני מטרים).
אני לא מבין למה לדעתך לא קיימת התפלגות נורמלית של גובה אנשים ?
רח וליזה:
התפלגות אכן נקראת נורמלית כי היא נורמלית.
זה עדיין לא אומר שהיא צריכה להיות בצורת הפעמון המתואר בדיוק על ידי פונקציה מסוימת.
כעיקרון – אין זה מובן מאליו שבכלל תהיה התנהגות שניתן לאפיין כ”נורמלית”.
משפט הגבול המרכזי הוא משפט חשוב שאומר שכשיש הרבה הגרלות עם התפלגות זהה אז ממוצע תוצאותיהן שואף להתפלגות נורמלית (בהגדרתה המתמטית) ככל שמספר ההגרלות גדל.
זה משפט יפה וחשוב והוא באמת מסביר מדוע – אם ניקח מדגמים בני הרבה מאד אנשים ונמדוד את הגובה הממוצע – ונחזור על התהליך פעמים רבות – יתפלגו הממוצעים השונים על פני עקומה המתקרבת להתפלגות נורמלית – ככל שגודל המדגמים יגדל.
עם זאת – זה לא יגרום לעקומת התפלגות גבהי האנשים להיראות כהתפלגות נורמלית!
לשם הדגמה – נניח עולם דמיוני שיש בו רק שני גבהים אפשריים של בן אדם – מטר ושני מטר בהסתברויות שוות.
אם תיקח מדגם של מאה אנשים ותחשב את ממוצע הגובה שלהם תקבל מספר בין 1 ל 2.
אם תיקח אלף מדגמים כאלה ותחשב את הממוצעים שלהם יתפזרו ממוצעים אלה על פני עקומת פעמון קרובה להתפלגות הנורמלית.
(למעשה יקרה עוד דבר – ככל שהמדגמים יהיו יותר גדולים ההתפלגות הזאת תשתנה כי השונות שלה תקטן וחלק יחסי גדול יותר שלהם יתרכז סביב ממוצע הגובה שהוא 1.5 מטר בדוגמה זו. ירידה זו של השונות הופכת את התמשכות העקומה עד מינוס אינסוף לפחות ופחות רלוונטית).
לעומת זאת – אם תיקח את אותם מאה אלף אנשים – גובהיהם לא יתפזרו על שום עקומת פעמון!
עדיין חלקם יהיו בגובה מטר וחלקם בגובה שני מטר. קרוב לוודאי שחלקים אלה יהיו די דומים במספר האנשים שבהם. בטוח שלא יימצא אף אחד שגבהו הוא 1.5 מטר למרות שבהתפלגות הממוצעים שעשינו דווקא 1.5 היה הגובה הממוצע בעל ההסתברות הגבוהה ביותר.
הסיפור עם הקוביות דומה.
אם תיקח אלף מדגמים של 100 הטלות זוג קוביות – יתפזרו ממוצעי מדגמים אלה על פני עקומה שדומה להתפלגות נורמלית.
אם תיקח מדגם אחד של 100,000 הטלות – סביר שהתוצאות תתפזרנה על פני משולש.
לכן – התפלגות נורמלית של הטלות זוג קוביות אינה מתקיימת.
לכן גם – התפלגות נורמלית של גבהי האנשים היא מפתיעה (אם היא קיימת אבל – לדעתי היא גם לא ממש קיימת וכמו במדידות של תופעות טבע רבות היא רק קירוב נוח. ההסבר האינטואיטיבי לכך שזה קירוב טוב מבוסס על ההנחה שהגובה של כל אדם מהווה בעצם ממוצע של הרבה מאד הגרלות בעלות התפלגות פחות או יותר זהה – דבר שיכול להיות מוצדק אם יש – נאמר – 100 גנים שלכל אחד מהם הרבה אללים פוטנציאלים ולכל הגנים השפעה דומה על הגובה)
ר.ח:
אני מסכים שבאופן גס היה ניתן לחשוב שכאשר בוחנים תופעות בטבע, ניתן באופן אינטואיטיבי לחשוב שערכים מסוימים יהיו מאוד שכיחים ואחרים פחות. אך לא די בכך בשביל לתאר התפלגות נורמלית.
לגבי משקל אנשים או צבעי עיניים – אישית איני רואה סיבה א-פריורית להניח שתופעות אלו ייתפלגו נורמלית (אך מעשית מסתבר שהרבה תופעות אכן מתפלגות כך).
מהם המשתנים המקריים שסכומם קובע את משקלו של אדם או את גובהו?
ליזה,
התפלגות נורמלית היא לא משהו מסתורי. הרבה פעמים ניתן למצוא לה הסבר. למשל כשיש תופעה הנובעת מצירוף של מספר גורמים בלתי תלויים , כתוצאה מהצירופים תתקבל התפלגות נורמלית. לדוגמא סכום קוביות. דוגמא אחרת משקל האנשים המתפלג נורמלי. בקצוות יהיו כאלה שמסיבות גנטיות + חוסר מזון יהיו סופר רזים ובצד השני כאלה שמסיבות גנטיות והתנהגותיות של אכילת יתר יהיו סופר שמנים. כל השאר יהיו באמצע. מה מסתורי כאן?
צבע עניים או גובה נגרמים ע”י מספר גנים ולכן צרופים שונים שלהם יביאו לצורות שונות. רק צרוף מאד נדיר יביא לגובה מעל שני מטר או מתחת למטר (באדם בוגר) אז שוב אין כאן שום פלא או מסתוריות.
ר.ח:
זו גם דרך להסתכל על הדברים, אך אני מסתכל על הדברים כך:
ישנם הרבה תופעות בטבע שמתפלגות על פי התפלגות מסוימת – זה דבר אחד שהוא מפתיע בפני עצמו.
עתה אחרי שגילו את התגלית המפתיעה הזו, החליטו לקרוא להתפלגות זו התפלגות נורמלית, מפני שאכן מסתבר שזו התפלגות מאוד נפוצה (אבל ישנם הרבה תופעות שאינם מתפלגות נורמאלית).
הדבר השני המפתיע אינו קשור ישירות לתופעות הנצפות בטבע אלא לעולם הוירטואלי של המתמטיקה. דבר זה הוא משפט הגבול המרכזי והוא אומר את הדבר הבא:
תיקח כמעט כל התפלגות שבא לך (אפילו על ידי שרבוט של התפלגות על דף) ועתה תתחיל לדגום דגימות מתוך ההתפלגות ולסכום אותם. הסכום הוא משתנה מקרי בפני עצמו והוא שואף להתפלגות, שבמקרה נקראת מורמאלית, ככל שנקח יותר דגימות.
המשפט המתמטי משמש לעתים כהסבר ל”נורמליות” של ההתפלגות ולעובדה שהיא מאוד נפוצה בטבע.
ליזה,
כנראה שאני מפספס פה משהו.התפלגות נורמלית נקראית נורמלית כי המון תופעות מתנהגות לפיה והיא נורמלית. אז מה מפתיע בנורמלי? בדרך כלל הלא נורמלי מפתיע.
ר.ח:
מה שמפליא(אותי לפחות) הוא שהדבר כלל לא תלוי בהתפלגות המשתנים המקריים אותם סוכמים (עד כדי התפלגויות בעלות תוחלת או שונות שאינם סופיים).
צריך לציין שהתפלגות הסכום שואפת בדיוק להתפלגות נורמאלית ולא רק למשהו שדומה כללית לפעמון.
ליזה, למה זה מפליא? אם יש מספר פרמטרים שאינם תלויים זה בזה זיוצרים תופעה מדידה יש להניח שזה מה שתקבל.
משולש כי יש מעט ערכים וזה קירוב, תעשה את אותו דבר עם אינסוף קוביות תקבל את הפעמון שלך. כל חישוב הסתברויות מבוסס על מה שיותר נסיונות. תזרוק מטבע 3 פעמים ולא תוכל להסיק כלום על ההסתברות לקבל עץ.
כמובן שגם משולש הוא “סוג של” פעמון.
לכן בעצם עולה השאלה – מה אתה רוצה לכנות פעמון.
כללית אפשר לתאר משתנים המתפלגים באופן שאפילו אינו נותן צורה סימטרית.
ר.ח:
אני מניח שאתה מכוון למשפט הגבול המרכזי שהוזכר כאן. אם משליכים אותו לדוגמאת הקוביות שנתת הוא אומר שסכום המספרים הוא אכן משתנה שהתפלגותו תתקרב להתפלגות נורמאלית ככל שניקח יותר קוביות.
מה שמפליא במשפט הוא שהוא תקף לגבי כמעט כל התפלגות שהיא של המשתנים אותם סוכמים (במקרה הקוביות היתה זו התפלגות אחידה על ערכי הקוביה)
עובדה זו משמשת לעתים כהסבר לנוכחות הרחבה של ההתפלגות בתופעות שונות בטבע. נהוג להניח למשל שרעש במדידות מתפלג נורמאלית, וההסבר שניתן הוא שהרעש הוא סכום של הרבה גורמים קטנים יותר.
הדבר לא תמיד מוצדק אך יש גם סיבה הנדסית להנחה זו והיא שההתפלגות הנורמאלית של רעש מפשטת מאוד מידול מתמטי של תופעות.
ר.ח:
לא.
אם תצייר לעצמך טבלה של 7X7 שבשורה העליונה תייצג (החל מן העמודה השנייה מימין) את תוצאת קובייה א ובעמודה הימנית תייצג (החל מן השורה השנייה מלמעלה) את תוצאת קוביה ב, תוכל למלא את משבצות הטבלה בסכום המתקבל בהטלה המיוצגת על ידי צירוף השורה והעמודה.
הסתברותה של כל משבצת בטבלה היא 36 / 1.
לכן 2 מתקבל בהסתברות 36 / 1
3 מתקבל בהסתברות 36 / 2
4 מתקבל בהסתברות 36 / 3
5 מתקבל בהסתברות 36 / 4
6 מתקבל בהסתברות 36 / 5
7 מתקבל בהסתברות 36 / 6
8 מתקבל בהסתברות 36 / 5
9 מתקבל בהסתברות 36 / 4
10 מתקבל בהסתברות 36 / 3
11 מתקבל בהסתברות 36 / 2
12 מתקבל בהסתברות 36 / 1
אם תצייר את הגרף תקבל משולש
אתה המתימטקאי. נראה לי שניתן להוכיח שכל תופעה המורכבת ממספר פרמטרים תתנהג בצורת פעמון.
לדוגמא קוביה אחת תראה התפזרות שווה לכל הערכים אולם שתי קוביות תראינה התפלגות פעמון כשבמרכז 7 ובצדדים 12 ו 2. האם אני צודק?
ר.ח:
אינך מתפלא כי לא “נכנסת לראש של הכתבה”.
כפי שאמרתי – כל הפליאה המובעת בכתבה היא על הדמיון המתמטי בין התופעות שאינן קשורות.
כפי שהסברתי – הפליאה לא ממש מוצדקת כי הדמיון המתמטי הזה לא ממש קיים והתיאור המתמטי של עקומת הפעמון אינו תיאור מדויק של המציאות אלא רק קירוב נוח.
אתה רואה ב”פעמון” רק תיאור כללי של המראה של העקומה ולכן אינני מתפלא על שאינך מתפלא 🙂
הרי כל הפליאה (שלטעמי אינה מוצדקת) נובעת מייחוס חשיבות מוגזמת לפונקציה המתמטית שנבחרה.
אני לא מבין מה מפליא. אותי היה הרבה יותר מפליא אם רוב התופעות היו תופעות קיצון כלומר הפוך מפעמון שרוב הדגימות היו מתרכזות בקיצון ומיעוטן במרכז או תופעה שמספר הדגימות בכל ערך שווה.
ר.ח.:
העניין כאן הוא שהמאמר מדבר על העקומה המתמטית שנקראת עקומת הפעמון.
כל העניין הוא הרי מתמטי וזה מקור הפליאה לכאורה.
אני מצטט: … טוב – אני מתחרט ולא מצטט… הלכתי לבחור משפט לציטוט וראיתי שכמעט כל משפט אומר זאת ואני מתקשה לבחור.
צבי 20, ההתייחסות שלך הפוכה להבנה שלי, אולי כי אתה פיזיקאי ואני ביולוג ובזה בדיוק מתבטא ההבדל בין שני התחומים האלה :). אתה טוען “ישנן הרבה צורות שנראות כמו פעמון אבל לא מקיימות את אותה משוואה.” אולם אני רואה את זה בדיוק הפוך – יש המון תופעות בטבע שמתפלגות בצורת פעמון אולם המשוואה שהצגת לא מתארת אותן בדיוק כי היא לא מניחה חסמים.
מה שאני רוצה לאמר כאן זה שהתופעות לא מתנהגות ולא צריכות תהתנהג לפי משוואה אלא שהמשוואה המלאכותית אמורה לתאר את התופעות ולנבא את ההתנהגות שלהן.
או קיי, עם זה אני מסכים.
חשוב להדגיש כי המכניקה הסטטיסטית לפחות בראשיתה הייתה קלאסית לגמרי (אם אני לא טועה פארדוקס גיבס בחישוב האנטרופיה של גז אידיאלי היה המקום הראשון בו נכנס רעיון קוונטי) ופשוט, כפי שציינת הבינה כי קשה וחסר טעם לחשב את מסלולה של כל מולקולה ומולקולה
צבי
לא נסיתי לטעון כי לעקומת הפעמון עצמה יש השלכות ישירות למכניקה סטטיסטית או לקוונטים, למרות שיש כאלו, לפחות לפיסיקה סטטיסטית כמו שציינת. ההבנה שהגיעה בתחילה עם הפיסיקה הסטטיסטית הייתה כי לעתים אין לנו היכולת לעקוב אחרי כל דרגות החופש של מערכת ועלינו להתייחס אליהם באופן סטטיסטי קרי להתייחס לגודל הממוצע לסטיית התקן או לקורלציות. ההבנה כי אין לנו נגישות לכל דרגות החופש או כי הללו הם בעצם לא נקבעים על ידי חוקים דרמינסטיים התבססה בתורת הקוונטים. תפיסה זו שונה מהותית לטעמי מזו של המכניקה הקלסית בה ניתן תיאור מלא של המערכת בכל רגע נתון. עקומת הפעמון היא לטעמי כניסתה של הסטטיסטיקה אל הפיסיקה ולכן אני מייחס לה חשיבות.
ר.ח,
השם התפלגות פעמון מטעה – ישנן הרבה צורות שנראות כמו פעמון אבל לא מקיימות את אותה משוואה.
עקומת הפעמון עליה מדובר היא צורה של גאוסיאן (e^-x^2 עד כעדי הכפלה בקבוע נרמול) – צורה כזו ע”פ הגדרה אינה חסומה בין ערכים אלא משתרעת לאינסוף משני צדדיה).
אהוד,
הקישור שציינת בין עקומת הפעמון למכניקה הסטטיסטית מובן בהתפלגות מקסוול, או בפלקטואציות סביב נקודת שיווי משקל תרמודינמית. הייתי מעוניין שתסביר מדוע אתה טוען כי הבנת עקומת הפעמון הייתה משמעותית כל כך לתורת הקוונטים – שים לב כי במכניקה הסטטיסטית הקלאסית לא הוכנסה למדע אקראיות אמיתית – התפיסה היא עדיין דטרמנטיסטית לגמרי וזאת בניגוד לתורת הקוונטים ולכן לדעתי זה שונה למדי.
מדע עוסק באידיליזציות. המדע משווה את התופעות בטבע למודלים אידאליים שאינם מתקיימים בפועל.לדוגמא: גוף הנופל על פמי כדור הארץ אינו נופל נפילה חסרת חיכוך הוא אינו נקודתי ולכן פועלים
עליו מומנטים ופועלים עליו כוחות משיכה של גופים שונים בינהם הירח. למרות כל אילו המודל הפשוט של
גוף נופל על פני כדור הארץ הינו מודל של נקודת מסה הנעה בהשפעת הגרויטציה של כדור הארץ ללא חיכוך. אותו סוג של אידאליזציה המדע מבצע גם לגבי הרעש בניסוי ומקרב אותו להתפלגות אידאלית קרי עקומת הפעמון. עד כמה הקירוב טוב זה תמיד תלוי במקרה אותו בוחנים.
המענין לטעמי בנושא עקומת הפעמון היא ראשית , ההתקדמות הטכנולוגית שאיפשרה בהרבה מקרים להתחיל לדבר על דיוק בניסויים. כאשר התחילו להבחין באי-התאמות בין מודלים לניסויים והתחילו לכמת את אי-ההתאמה הזו החלו להבין את החשיבות של הסטטיסטיקה במדע.שנית, לטעמי הבנה זו הובילה לפיסיקה הסטטיסטית ומאוחר יותר לתורת הקוונטים. עקומת הפעמון היא ראשית כניסתה של האקראיות למדע!
יהודה ומכ*אל, המון תופעות בטבע מתנהגות בצורת פעמון עם ערכי מינימום ומקסימום. מי אמר שפעמון צריך ללכת לאינסוף?
קחו למשל את התפלגות הגובה של בני אדם שמתחילה ממספר עשרות ס”מ בתינוק כגבול תחתון ועד נניח ל- 2.5 כגבול עליון עם קרוב ל 7 מיליארד דגימות שמסתובבות בין הערכים האלה בצורת פעמון.
הכוונה בשאלתי לא הייתה לגבי המתמטיקה שלגביה מסכים שיש פעמון
לגבי שאר תשובתך- יש כאן חומר למחשבה.
יהודה
תלוי מה כוללים במונח “טבע”.
אני מניח שאם נבקש מאנשים לבחור באופן אקראי מספרים (חיוביים או שליליים – ככל שתחפוץ נפשם) – נקבל התפלגות פעמון טובה למדי.
כמובן שגם אז יהיה מדובר בקירוב כי זה יהיה פעמון ש”מפוזר” על מספר סופי של ערכים בשעה שהפעמון האמתי הוא רציף אבל אני מניח שבכל זאת מותר יהיה להתייחס לזה כפעמון (שהרי כל סטטיסטיקה שאי פעם נערוך תתבסס על מספר סופי של דגימות).
האם ניסוי כמו זה שתיארתי צריך להיקרא תופעת טבע? זה כבר עניין של החלטה.
באופן כללי – ההתפלגות של אותה תופעה יכולה להיראות באופנים שונים כתלות בגודל הנמדד.
אני יכול למדוד תופעה שמניבה רק ערכים חיוביים אבל אותן תוצאות (מספריות) יכולות להיות מיוצגות על ידי הלוגריתם של התופעה ואז תתפלגנה על פני כל הישר הממשי.
יכול, לכן, להיות – שיש תופעות טבע שהתפלגותן אינה נורמלית כשמסתכלים עליהן באופן מסוים, בשעה שבאופן הסתכלות אחר היא תהייה נורמלית.
למיכאל
אמרת כמעט כל התופעות בטבע אינן מתנהגות כמו הפעמון
אני מנסה למצוא תופעה אחת בטבע שכן פועלת כמו פעמון מדוייק ולא מוצא
האם ייתכן וכל התופעות בטבע אינן מתנהגות כמו פעמון, ותמיד נצטרך להשתמש בקרוב כל שהוא?
שבת שלום
סבדרמיש יהודה
כמעט כל התופעות בטבע אינן מתנהגות ואינן יכולות להתנהג לפי פעמון מדויק.
לחלק גדול מהן יש מינימום שלא ניתן לרדת מתחתיו (למשל מינימומים שקשורים באפס המוחלט) ועקומת הפעמון אמורה, כידוע, להמשיך עד אינסוף לכל צד.
מדובר בסך הכל בקירוב נוח שחלק מיעילותו נובע מכך שבגבול – ההתפלגות הבינומית (שפעמים רבות ממש קל להסביר את סיבתה) – מתקרבת להתפלגות הנורמלית.
צריך לקרוא את ההודעות לפני שלוחצים שלח.
קומפקסי=קומפלקסי.
חרדי הוא אוילר של ימינו.
רק מה, הרעיון ישן טיפה – בן כ250 שנים.
דוגמא לזה היא כמובן הנוסחה:
e^(i*pi)+1=0
תראה מה זה – יש שם e, פאי, מספר קומפקסי i, וגם 0,1, יש בה חיבור, כפל, חזקה ושיוויון!
יש אלוהים!
אההה,
סיבה כזו אתה מחפש,
מצויין – אתה יודע מה היא ולי אין כוונה להכנס איתך לעימותים תיאולוגים עקרים
שבת שלום (או בשבילך בהתחשב בשעה – שבוע טוב)
מר צבי,
אם אין לך קושי למה אינך מסביר את הסיבה.
לא מדובר בהוכחה או בחישוב אינטגלים
המדובר ב—” ס י ב ה ” / “ל מ ה ” / ” מ ד ו ע ”
מדוע ולמה ומאיזו סיבה התפלגויות נורמאליות במציאות הפיסית
מבוטאות בביטויים המתמטיים הללו.
מהו הקשר העמוק ל-PI ומהו הקשר העמוק ל-e
אל תוכיח אלא תסביר את הסיבה לקשר הזה האם תוכל.
מר חרדי,
כמובן שאין כל קושי להסביר אצ שני הדברים:
1. השם “פעמון” אינו אלא כינוי למה שהוא למעשה הפונקציה e^-x^2
2. שטחו של הפעמון ניתן למציאה פשוט ע”י אינטגרציה
רענן, (4)
בטח צחקת צחוק מרענן כשכתבת.
לפי שיטתך ים זה אוסף של שלולויות ואדם זה גוש של חומצות אמינו
קשה יותר להסביר את סיבת הקשר של הפעמון לפונקציה האקספוננציאלית e^-x^2
ואת העובדה ששטח הפעמון הנ”ל הוא PI^0.5
משה:
אני מסכים שראוי לציין בהקשר זה את משפט הגבול המרכזי אך הוא אינו פותר את כל התעלומה.
לצורך העניין נסתכל על ערימת אבנים מבולגנת גדולה מאוד מאוד. עתה נבקש מאנשים לבנות מגדלים על ידי הנחת אבן על אבן, כל מגדל מ100 אבנים שנלקחו באקראי מהערימה. משפט הגבול המרכזי אומר לנו שהתפלגות גבהי המגדלים תתקרב להתפלגות הנורמלית (ותתקרב יותר להתפלגות זו ככל שנבנה מגדלים מיותר אבנים).
התעלומה עדיין נשארת כאשר בוחנים גבהים של אנשים למשל (מהם אבני הבניין הקובעות את גובהו של אדם?) או תופעות מסוג אחר שמתפלגות נורמלית.
כימיה זו פיזיקה ברמה גבוה.
כימיאים הם פיזיקאים ברמה נמוכה.. 🙂
אני לא מסכים שגיל הנישואים בבלגיה ובצרפת היא לא תופעה פיזיקלית, זאת כן תופעה פיזיקלית. כל דבר ביקום זה תופעה פיזיקלית כולל מחשבות שמרגישות כמו דבר לא פיזיקלי. זה רק פיזיקה ברמת סיבוכיות גבוה יותר. פיזיקה כימיה וביולוגיה זה הכל בעצם פיזיקה. כימיה זאת פיזיקה ברמת מורכבות גבוה יותר וביולוגיה זאת רמת מורכבות פיזיקלית עוד יותר גבוה.
כדאי לציין שהעובדה שעקומת הפעמון חוזרת ומופיעה במקומות רבים ושונים היא תופעה מובנת היטב ומוסברת ע”י “משפט הגבול המרכזי”
http://en.wikipedia.org/wiki/Central_limit_theorem
שאותו כל בוגר אוניברסיטה במדעים או הנדסה אמור לדעת.
רן, בחיאת דינק, תשתמש רק בשם משפחה שלו.
אני לא יודע מי זה, אבל השם “אדולף” לא ממש עושה לי קונוטציות טובות….