איך משלבים שעשוע מתמטי וקישוט לסוכה?

קישוטמתיקה לסוכה – טבעת מוביוס.

אמיר ברנט האגודה הישראלית לאסטרונומיה

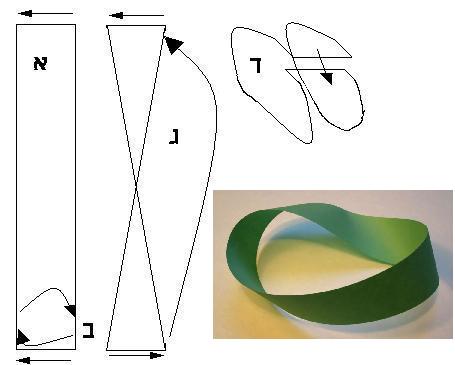
בגדול: איך מכינים את הטבעת. בקטן- מראה טבעת מוביוס – ויקיפדיה

מי שבכל זאת חוגג את החג, ולו מטעמי שמחה לשמה ולאו דווקא מטעמים דתיים, מוזמן לשלב את המתמטיקה עם מנהג קישוט הסוכה.

במקום לקנות קישוטי סוכה כמו שיש לכולם – נעשה קישוט כמו פעם, מנייר מספריים ודבק. אחר כך ננסה להבין מה כל כך מוזר בטבעות מוביוס.

מצרכים:
דף נייר גדול עדיף בגודל 3A – אפשר מנייר עיתון מומלץ נייר שצבוע בשני צדדיו בצבע שונה, וכדאי שיהיו כמה דפים. מספריים (מומלץ שיהיו עם השגחת מבוגר) וכן דבק פלסטי פשוט מכל סוג (מומלץ כזה שבאמת מדביק).
הוראות הכנה:
את הדף נגזור לרצועות ברוחב של בין 8-15 ס"מ על הצד הארוך יותר של הדף (א).
ברצועה הראשונה שלנו נבחר את אחד הקצוות המרוחקים ונסובב אותו כך שהפינה הימנית תהיה עתה השמאלית ולהפך (ב).
השלב האחרון יהיה להדביק את שני הקצוות (זיכרו, אחד מהם עבר סיבוב בודד!) ממש כשם שהיינו מדביקים ליציאת טבעת בקישוטי הסוכה שמוכרים מבית הספר (ג), (ד – יצירת טבעת רגילה), עתה נמתין שהדבק יתייבש. והרי לנו טבעת מוביוס, ממש כמו טבעת רגילה שאפשר להכין לטובת קישוטי הסוכה, אך בהיפוך אחד, וזה הוא כל ההבדל.
אוגוסט פרדיננד מוביוס מתמטיקאי ואסטרונום גרמני (1790 – 1868August Ferdinand M�bius ) גילה והונצח בטבעת המוביוס. בניגוד לאמרה המוכרת, לא לכל דבר יש שני צדדים. בחיי היום יום אנו רגילים שלקוביה יש שש פאות ולמטבע שני צדדים ואילו, לטבעת המוביוס יש רק צד אחד, לא מאמינים? בואו נבדוק: מאחת הרצועות הנוספות ניצור טבעת רגילה (כמו ב(ד)) ונחליק אותה לאורך כף היד תוך כדי סימון קו עם טוש על צד הנייר שפונה אלינו באמצעו, והנה לאחר רגע הקו חזר לתחילתו, מהצד הפנימי – אין כל רמז למגע עם הטוש. עתה נעשה את אותו הדבר עם טבעת המוביוס שלנו, נסמן קו לאורכה באמצע הטבעת, האם דבר לקח יותר זמן? האם הטוש הופיע עתה גם בצד הפנימי?

עכשיו נהיה קצת יותר אכזריים אל הטבעות שלנו, הגיע הזמן לגזור! נתחיל בגזירה כ2 ס"מ מצד הטבעת הרגילה ונגזור במקביל לצד בניסיון לחלק אותה לשתי טבעות, בסיום, קיבלנו טבעת דקה וטבעת עבה יותר, לא מרשים במיוחד… אך מה יקרה כאשר ננסה זאת עם טבעת המוביוס? ה-פ-ת-ע-ה! אחר כך נכין טבעת מוביוס נוספת ואותה הפעם נגזור באמצע, כדאי להכין מרצועות הנייר הנוצרות טבעות מוביוס נוספות שבהן נבצע היפוך נוסף (ב) ובטבעת אחרת נוסיף שני היפוכים ואף יותר, וגם אותן נגזור בצורה דומה. האם אפשר למצוא קשר בין מספר ההיפוכים ותוצאת הגזירה? מה ההבדל בין מספר זוגי ואי זוגי?

כמו שראינו בניסיון הראשון בעוד שלטבעת רגילה יש שני צדדים (ולכן הטוש צבע רק צד אחד) בטבעת המוביוס, סיבוב הקצה גרם לכך שצביעה לאורך הצד מאפשרת להעביר את הטוש לאורך כל הדף, כלומר לטבעת רק צד אחד! במשך שנים טבעות מוביוס נחשבו כשיגעון מתמטי חסר כל יישום אבל הן שימשו לקלטות המקליטות בצורה מחזורית, לדיו למכונות כתיבה וכן למסועי שינוע – דבר שאיפשר לנצל את כל אורכו ולא רק צד אחד לו היה מעוצב כטבעת רגילה.

סוכות שמח והכנה מהנה!