המערכות הקוונטיות נמצאות בשלב "המחשבים הקטנים והרועשים." עד אשר נייצר מערכות קוונטיות חפות מרעשים, עבודה רבה נעשית בשילוב מערכות קלאסיות בדגש על אלגוריתמים שיאפשרו לבצע חישובים קוונטים במערכות קיימות
מאת: תמוז דנציג, דוקטורנט לאלגוריתמים קוונטיים
בטח שמעתם רבות על מחשבים קוונטיים, שלפני חמש עשרה שנה נשמעו כמו מדע בדיוני. כיום, מעצמות, מדינות קטנות וחברות ענק משקיעות סכומי עתק במרוץ למחשב הקוונטי הראשון שיבצע חישובים מעשיים. למרות היקף המחקר העצום בתחום, נפח החישוב ובעיקר הרעש במערכות הקיימות כיום אינם מאפשרים להגיע ל״עליונות קוונטית״, כלומר שיפור של המחשב הקוונטי על המחשב הקלאסי בפתרון בעיות מסוימות. התקווה היא שבעשורים הקרובים הטכנולוגיה הקוונטית תשתפר, ומחשב קוונטי יזכה ליתרון מובהק. עד אשר נייצר מערכות קוונטיות חפות מרעשים, עבודה רבה נעשית בשילוב מערכות קלאסיות בדגש על אלגוריתמים שיאפשרו לבצע חישובים קוונטים במערכות קיימות. העוסקים בתחום מכנים את התקופה הנוכחית כ״עידן המחשבים הקטנים והרועשים״ (ובקיצור,NISQ-Era [1]). אחת השיטות המבטיחות לבצע חישוב קוונטי בעידן הנוכחי היא מעגלים היברידיים קוונטיים-קלאסיים, בהם הפוסט הזה יתרכז [2].
נזכיר מפוסטים קודמים כי חישוב קלאסי מתבצע באמצעות שערים לוגיים (ראו קישור [6]); באנלוגיה לכך, חישוב קוונטי מתבצע באמצעות שערים קוונטיים המופעלים על הקיוביטים, אלו הם הביטים של המחשב הקוונטי [7]. שער קוונטי הוא פעולה שמשנה את פונקציית הגל הקוונטית של המערכת כמו סיבוב, הוספת פאזה, יצירת שזירה בין קיוביטים שונים וכו׳.
כיום, כמות הקיוביטים במחשבים הקוונטיים מוגבלת. המחשב המוביל מבחינת כמות הקיוביטים, מכיל רק כ-127 כאלה . הקיוביטים הללו רועשים, והרעש מתגבר בצורה אקספוננציאלית עם הגדלת מספר השערים הקוונטיים המופעלים על הקיוביטים, אשר משנים את המצב הקוונטי של המערכת. חשבו על המשחק "טלפון שבור", שבו השחקן הראשון מתחיל עם מסר מסוים, וכל שחקן מגדיל את ההסתברות לשגיאה. כל שחקן משנה מעט את המסר המועבר, ובסוף מקבלים מסר שונה לגמרי. אם חמישה שחקנים משחקים, סביר להניח שהמסר הסופי יהיה קרוב למסר הראשוני – מה שמקביל למצב קוונטי שעבר מעט פעולות מאופיין ברעש נמוך. לעומת זאת, אם יהיו חמש מאות משתתפים, אין ספק שלא יהיה שום קשר בין המסרים. בכך צריך להיות זהירים, שכן מעט פעולות אינן מספיקות לחישוב של דברים מורכבים.
קיימות בעיות רבות שמחשב קלאסי מתקשה לבצע בזמן סביר. בין המפורסמות היא בעיית הסוכן הנוסע (בעיית אופטימיזציה שבה יש למצוא את הדרך המהירה ביותר בין ערים רבות), בעיות לוגיסטיות כמו שרשראות אספקה, חיזויים כלכלים של השוק, בעיות מתחום הכימיה כמו חקר מולקולות גדולות, יצירת תרופות חדשות, ועוד. אז איך עושים את זה עם מחשב קוונטי בעידן ה-NISQ? על מנת להתגבר על הרעש ולבצע חישובים תוך ביצוע מספר מינימלי של פעולות, פורסמו שני אלגוריתמים היברידיים המשלבים מחשב קוונטי ומחשב קלאסי ומהווים חלוצים בתחומם. האלגוריתם המשמש לפתרון בעיות אופטימיזציה נקרא Quantum Approximate Optimization Algorithm (QAOA) [3], והאלגוריתם המשמש בעיקר למציאת מצבי היסוד של מולקולות נקרא Variational Quantum Eigensolver (VQE) [4]. נציין ששני המאמרים פורסמו בשנת 2014, תזכורת לכך שהתחום מתפתח במהירות אדירה. כל כך אדירה, שהאלגוריתמים הללו כבר מיושמים במחשבים הקוונטיים המתקדמים ביותר שישנם כיום [5].
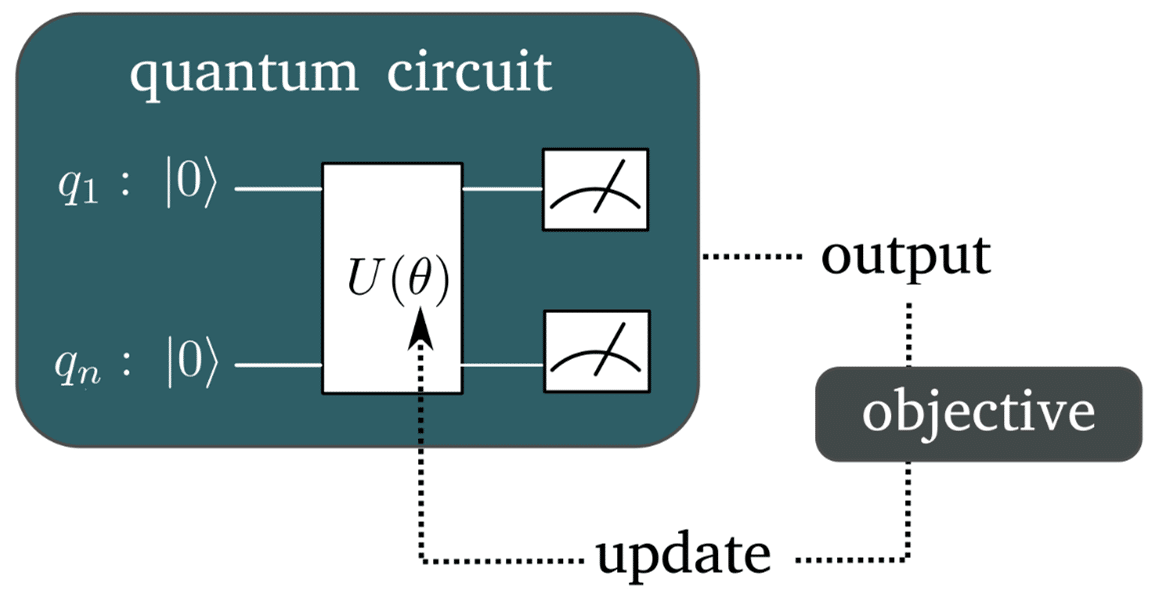
המבנה של האלגוריתמים ההיברידיים מתואר באיור המצורף. בצד השמאלי מוצג המעגל הקוונטי בו מאותחלים הקיוביטים במצב היסוד (מסומן כ-|0⟩). לאחר מכן, סט השערים הקוונטיים פועלים לשינוי המצב הקוונטי (מסומן כ-U(θ)) ואז מתבצעת מדידה. θ מהווה סט של פרמטרים הניתנים לכיוונון באופן רציף. הפתרון לבעיה יתקבל כאשר הפרמטרים הנכונים יוזנו למערכת, ומציאת פרמטרים אלו היא החלק הקלאסי במערכת ההיברידית. לאחר כל חישוב קוונטי מבצעים מדידה, ואת תוצאות המדידה (output) מכניסים לפונקציית המטרה (objective). תפקידה של פונקציית המטרה הוא לתת מדד לאיכות התוצאה שהתקבלה. תפקיד האופטימייזר (update) לעדכן את הפרמטרים לפני הרצה נוספת של המעגל המשולב למציאת מינימום של פונקציית המטרה. מציאת הפרמטרים מתבצעת באמצעות שיטות מלמידת מכונה כמו gradient descent (שיטת שינוי פרמטרים למציאת מינימום עבור פונקציית המטרה)[8], ושיטות נוספות. המעגל המשולב חוזר על עצמו באופן איטרטיבי עד לקבלת מינימום.
בחירת השערים הקוונטיים U(θ) היא נושא רחב וראוי לפוסט משל עצמו. בחירה נכונה של סוג השערים, סדר פעולתם וכיצד מפרשים את המדידה משפיעה על מהירות ואיכות החישוב. תכנון שערים טוב מתמקד בבעיה אותה רוצים לפתור ונובע מתוך תיאוריה פיזיקלית. לדוגמא שיטת Hartree-Fock היא שיטת קירוב למציאת מצב היסוד בבעיות של גופים רבים. על ידי שימוש בעקרון הווריאציה אפשר לקבל פתרון של פונקציית הגל ואת האנרגיה של המערכת, ששניהם קירובים לגדלים המדויקים. באלגוריתם VQE משתמשים בשיטה זו למציאת מצב היסוד של מולקולות.
בחירת מבנה המעגל הקוונטי של QAOA, מבוסס על חישוב קוונטי-אדיאבטי (Adiabatic Quantum Computation)[9]. בחישוב קוונטי-אדיאבטי המערכת מתוארת על ידי המילטוניאן התלוי בזמן העובר ממצב יסוד ידוע למצב יסוד של המילטוניאן המגדיר את הבעיה, המעבר להמילטוניאן החדש מהווה פתרון הבעיה. אם זמן החישוב ארוך מספיק הקירוב האדיאבטי תקף. בפועל ככל שמספר השערים גדל, גדלים הסיכויים למדוד את מצב היסוד הרצוי – זאת בהנחה שהחישוב הקוונטי חף מרעש. כפי שכבר הבנתם, לא ניתן להזניח את הרעש במערכות קוונטיות, אך אלגוריתם QAOA מציע סט קטן של שערים ופרמטרים שיאפשרו להגיע לפתרון מקורב וטוב מספיק, על אף שהוא לא יעמוד בקריטריון האדיאבטי. QAOA משתמש בהמילטוניאן התלוי בזמן בתוך המעגל הקוונטי, אך במקום ההתפתחות הרציפה בזמן, ישנו סט הפרמטרים. לכן, נחשב QAOA לאחד האלגוריתמים ההיברידיים המבטיחים [10]. למרות השימוש בז'רגון הפיזיקלי, מקובל לפתור באלגוריתם זה גם בעיות שאינן פיזיקליות, כגון בעיות בקומבינטוריקה, בכלכלה ועוד.
מערכת היחסים בין המחשוב הקלאסי לרעהו קוונטי היא הדדית. כפי שראינו, חישוב קלאסי הוא תבלין שרק משפר את החישוב הקוונטי. באופן דומה, רבים מהתחומים בלמידת מכונה ״קלאסית״ עברו הסבה לאלגוריתמים היברידיים [11]. למתעניינים מומלץ לקרוא על התחום שנקרא רשתות נוירונים קוונטיות (Quantum Neural (Network [12] ועשה רעש רב. מאז פרסום VQEו- QAOA מגוון האלגוריתמים ההיברידיים התרחב מאוד, ורבים תולים תקוות בכך שאלגוריתמים אלו יהיו הראשונים להגיע ל-״יתרון קוונטי” על פני המחשב הקלאסי.
מקורות
[1] Preskill, John. "Quantum computing in the NISQ era and beyond." Quantum 2 (2018): 79.
[2] Bharti, Kishor, et al. "Noisy intermediate-scale quantum algorithms." Reviews of Modern Physics 94.1 (2022): 015004.
[3] Farhi, E., Goldstone, J., & Gutmann, S. (2014). A quantum approximate optimization algorithm
[4] Peruzzo, A., McClean, J., Shadbolt, P. et al. A variational eigenvalue solver on a photonic quantum processor. Nat Commun 5, 4213 (2014).
[5] Harrigan, Matthew P., et al. "Quantum approximate optimization of non-planar graph problems on a planar superconducting processor." Nature Physics 17.3 (2021): 332-336.
[6]https://he.wikipedia.org/wiki/%D7%A9%D7%A2%D7%A8_%D7%9C%D7%95%D7%92%D7%99
[7] https://en.wikipedia.org/wiki/Quantum_logic_gate
[8] https://en.wikipedia.org/wiki/Gradient_descent
[9] Farhi, E.; Goldstone, Jeffrey; Gutmann, S.; Sipser, M. (2000). "Quantum Computation by Adiabatic Evolution".
[10] Crooks, Gavin E. "Performance of the quantum approximate optimization algorithm on the maximum cut problem." arXiv preprint arXiv:1811.08419 (2018).
[11] Cerezo, Marco, et al. "Variational quantum algorithms." Nature Reviews Physics 3.9 (2021): 625-644.
[12] Abbas, A., Sutter, D., Zoufal, C. et al. The power of quantum neural networks. Nat Comput Sci 1, 403–409 (2021).
